6.1 数组与矩阵

6.1.1 数组

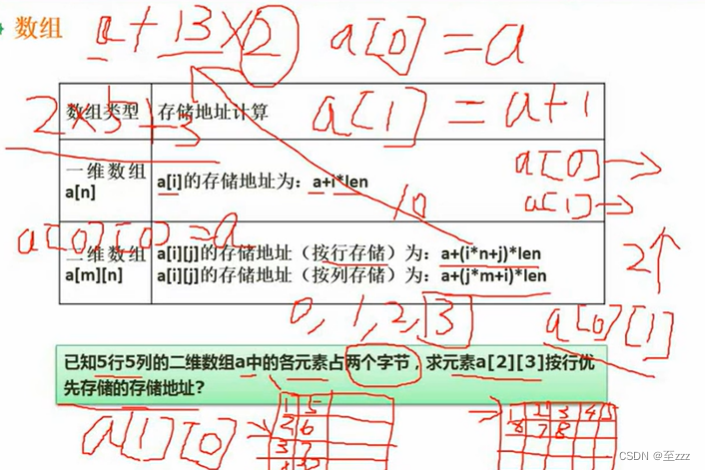
求存储地址

• 一维数组直接算
• 二维数组看清是按行还是按列存储

6.1.2 稀疏矩阵

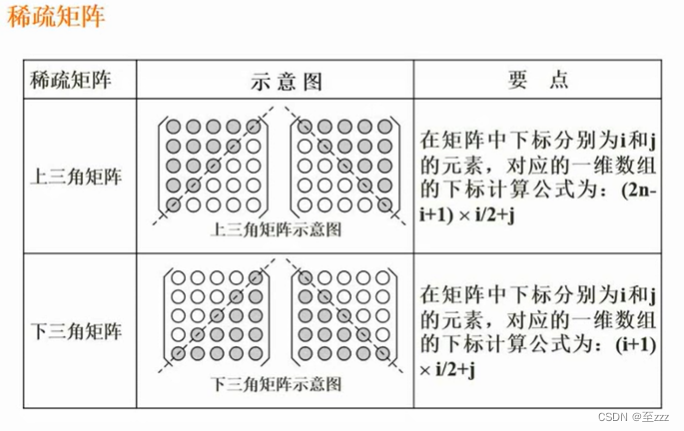
求对应一维数组下标公式，可以直接代两个元素进行验算

6.2 线性表

6.2.1 数据结构的定义

线性结构

• 线性表

非线性结构

• 树
• 图(可能存在环路)

6.2.2 顺序表与链表

6.2.2.1 定义

顺序表：采用一维数组的方式来存信息
链表：每个存储单元包含数据和指针

• 单链表：只有一套指针，头结点指向第一个元素，并依次指下去。
• 循环链表：与单链表的区别就是尾部有个指针直接指向头部。
• 双向链表：可以双向移动，一套指针从头指到尾部，一套由尾指到头部。

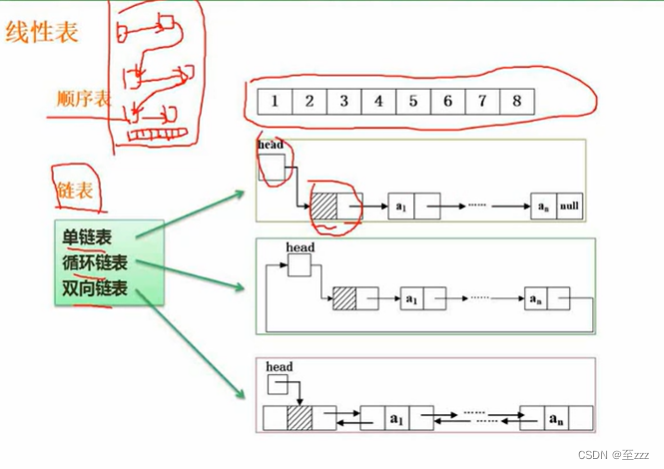
6.2.2.2 链表的操作

• 单链表删除结点：p->next = q->next
• 单链表插入结点：s->next = p->next;p->next = s->next

引入头结点的好处可以让所有的结点操作方式一致

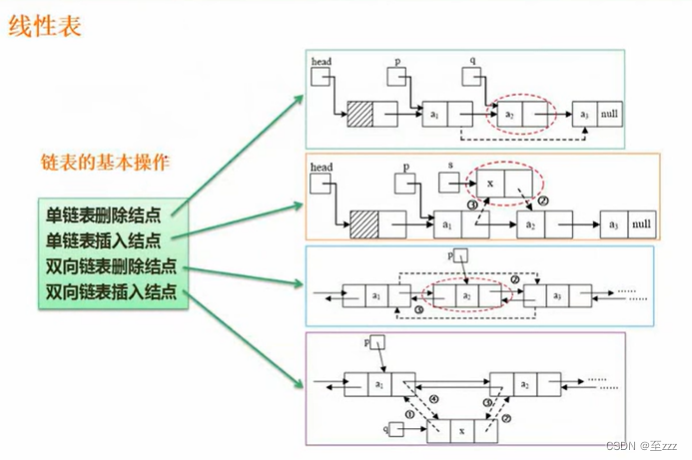
6.2.3 顺序存储和链式存储的对比

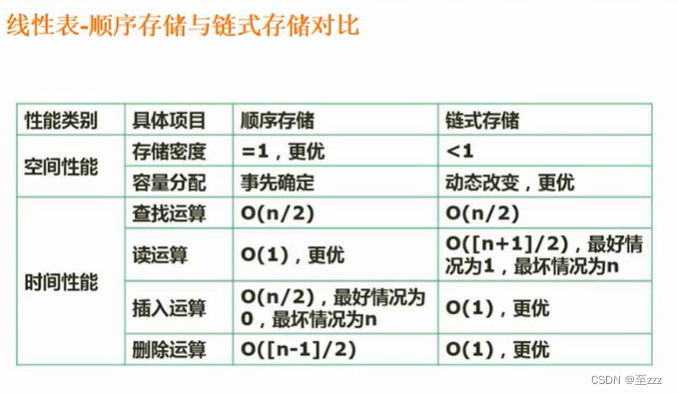
6.2.4 队列、循环队列、栈

队列：先进先出（又称先进先出表）
栈：先进后出

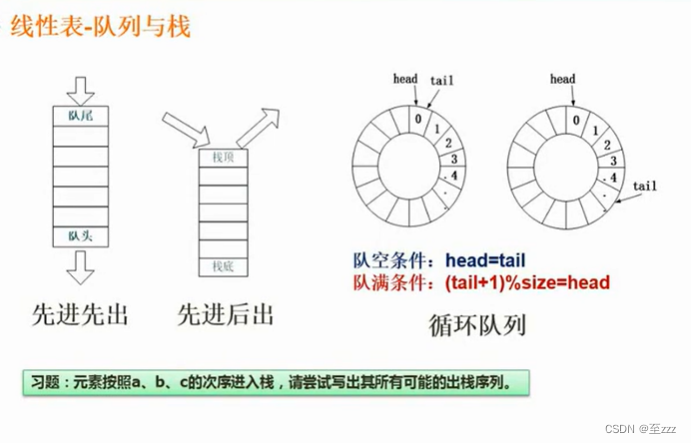
6.2.4.2 循环队列队空与队满条件

6.2.4.3 出入后不可能出现的序列练习

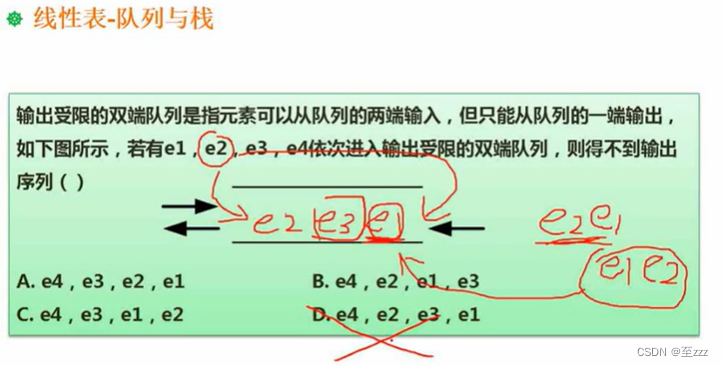
6.2.5 串

串是仅由字符构成的有限序列，是线性表的一种。

6.2.6 广义表

• 广义表是线性表的推广
• 广义表的元素即可以是单个元素(原子)，也可以是广义表（子表）
• 操作：
  *取表头head(LS)
  *取表尾tail(LS)

6.3 树与二叉树

6.3.1 基本概念

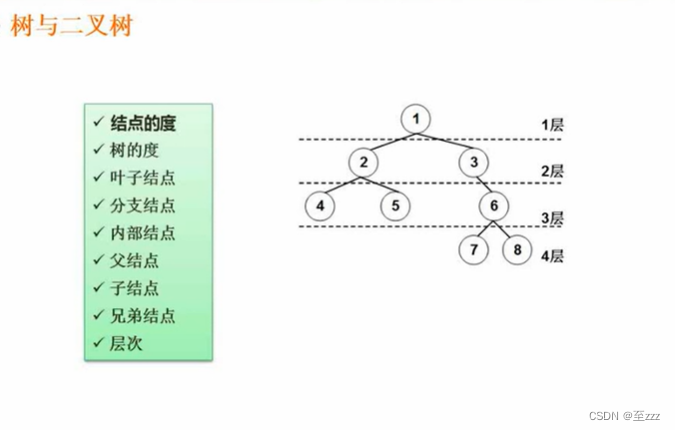
• 根：树最顶层的结点。即下图的结点1。
• 父结点（双亲结点）：元素的上一层。下图中结点1为结点2、3的父结点。
• 子结点：与父结点相反。
• 兄弟结点：与该结点同层。下图结点4是结点5的兄弟结点。6为堂兄弟结点。
• 结点的度：一个结点的子树的个数。下图结点2的度为2，结点7的度为0。
• 树的度：该树中结点的度最高的结点的度的个数。MAX。下图树的度为2。
• 叶子结点（终端结点）：度为0的结点。下图结点4、5、7、8。
• 内部结点（分支结点或非终端结点）：除根结点和叶子结点外。下图结点2、3、6。
• 结点的层次：根结点为第一层，依次往下。
• 树的高度（深度）：一棵树最大的层数。下图树的高度为4。

6.3.2 满二叉树与完全二叉树

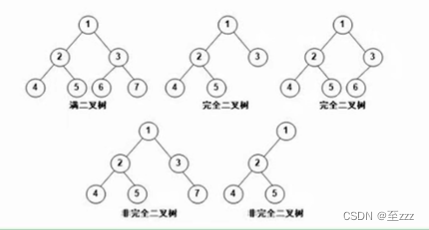
• 满二叉树：深度为k的二叉树节点个数为2^k -1，即所有的结点都是满的。

可以对满二叉树进行连续编号，约定编号从根结点自上而下，自左至右依次进行。

• 完全二叉树：除最底层外其余为满二叉树，最底层从左至右依次排列。

6.3.3 二叉树的重要性质

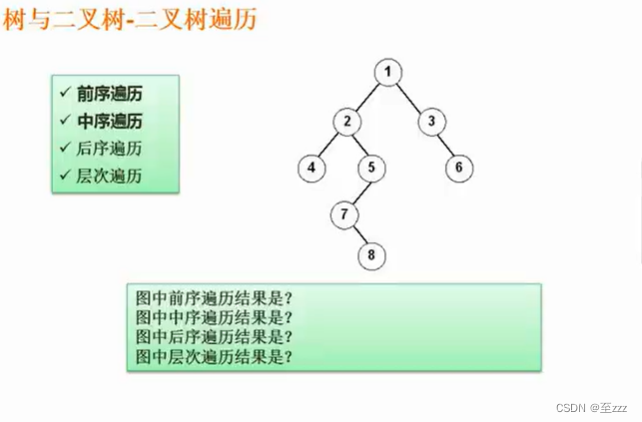
6.3.4 二叉树的遍历

三种遍历方式的区别就是根遍历的先后问题。

• 先序遍历：根左右
• 中序遍历：左根右
• 后序遍历：左右根
• 层次遍历：按顺序遍历

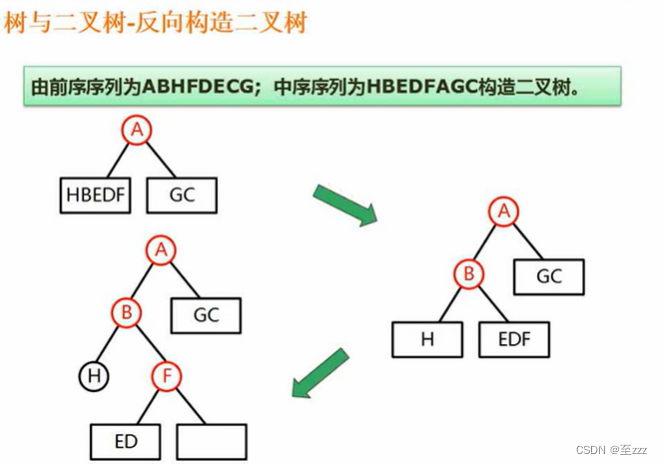
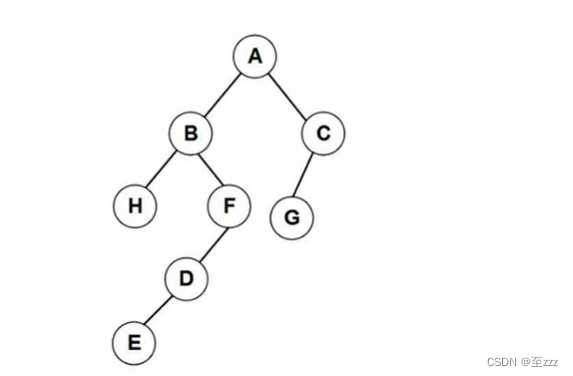
6.3.5 方向构造二叉树

给出二叉树的遍历序列，反向推出二叉树的结构

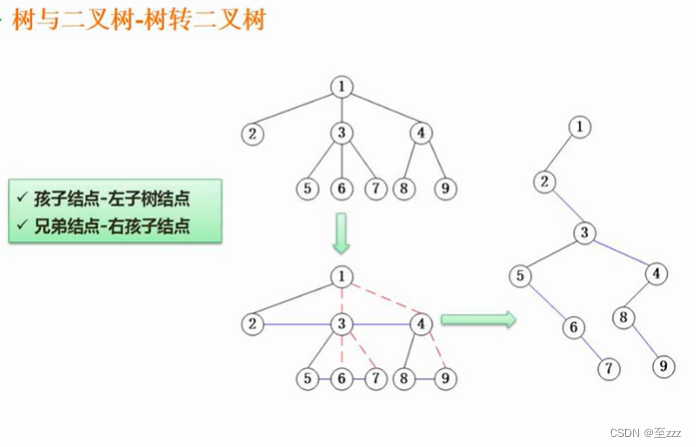
6.3.6 树转二叉树

1. 将兄弟结点相连。
2. 只保留第一个孩子结点与父结点的连线，其余全部断开，在旋转图可得

6.3.7 查找二叉树（排序二叉树）

对于每个结点，其左孩子结点小于根，右孩子结点大于根，称为查找二叉树。

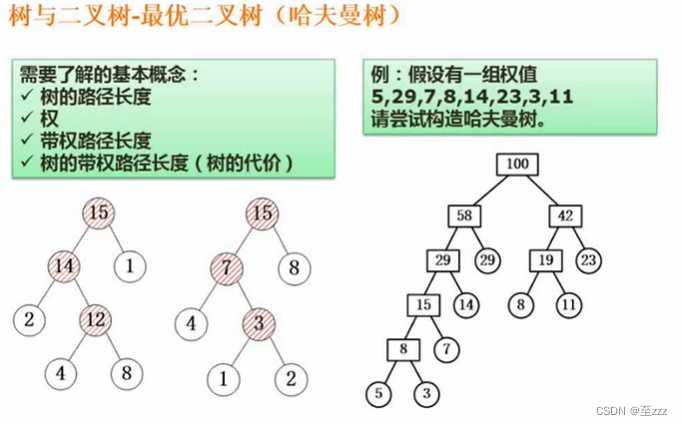
6.3.8 最优二叉树（哈夫曼树）

哈夫曼树是其叶子结点带权路径长度最短的二叉树。

• 带权路径长度：即路径长度乘权值，下图第一个二叉树的结点8的带权路径长度为8*3=24。
• 树的带权路径长度为其总和。

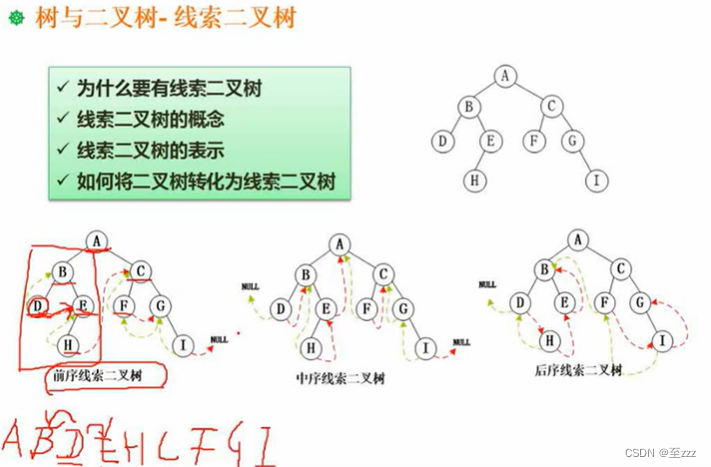
6.3.9 线索二叉树

在所有的叶子结点上标出其前驱和后继。需先求出其序列，才能写出对应的线索二叉树。

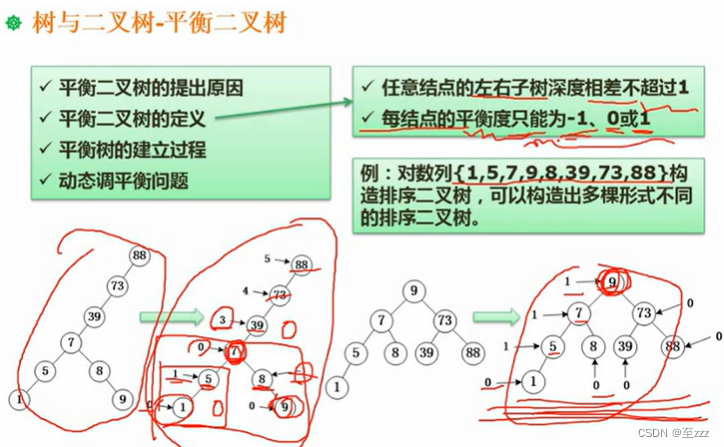
6.3.10 平衡二叉树

每个结点的平衡度只能为1、0、-1
平衡度为该结点的左子树深度减右子树深度的值

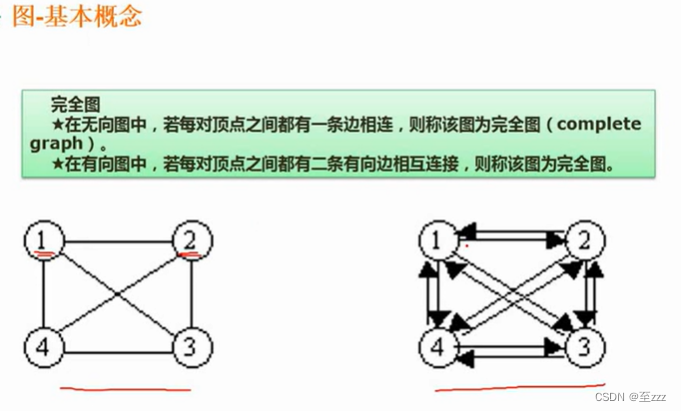
6.4 图

6.4.1 图的概念

无向图：连接的线无方向。
有向图：连接的线有方向。

6.4.2 图的存储方式

• 邻接矩阵：通路为1，无通路为0。

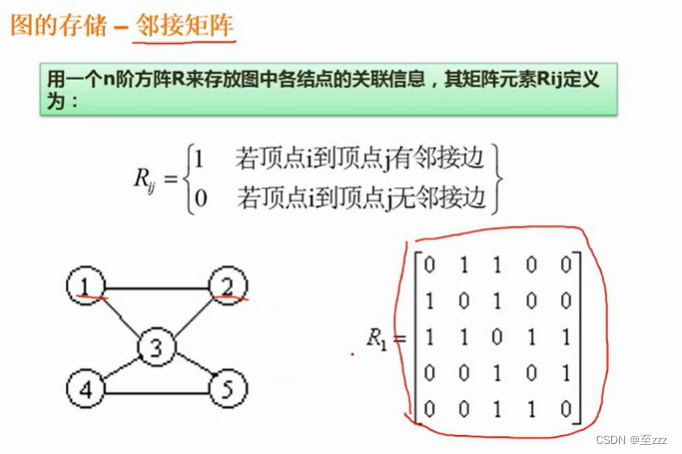
• 邻接表：邻接表会记录每个结点相邻结点的信息。用数组记录结点，用链表记录可以到的结点的情况。

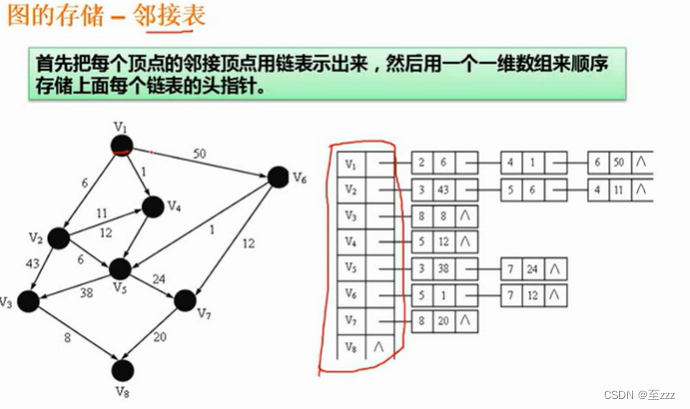
6.4.3 图的遍历

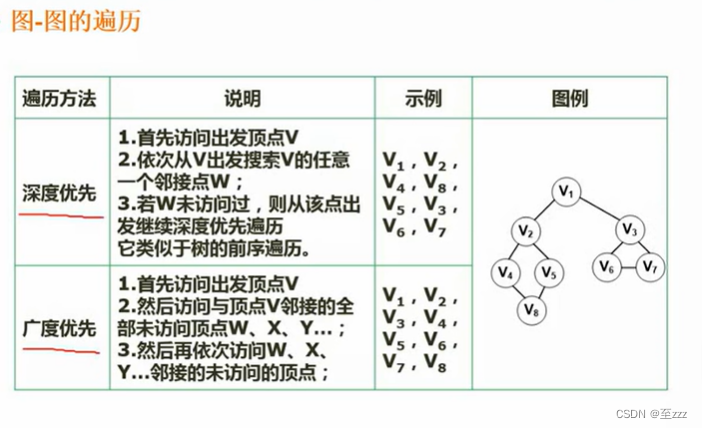
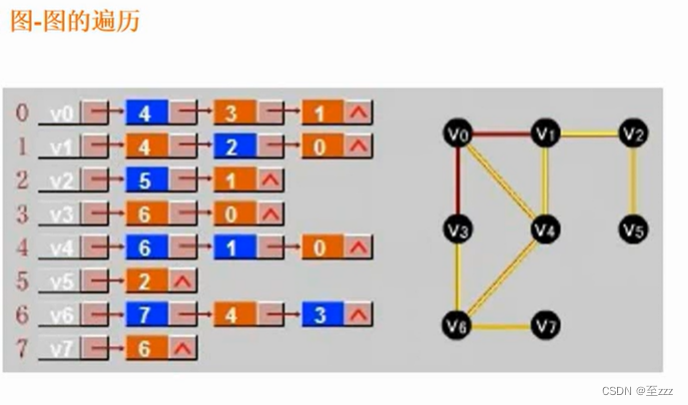
• 深度优先：根据线索，一层一层深入到底，直到无法继续访问再退回进入下一个分支。
• 广度优先：把一个结点的所有相邻的结点访问完，再进入下一个层次。

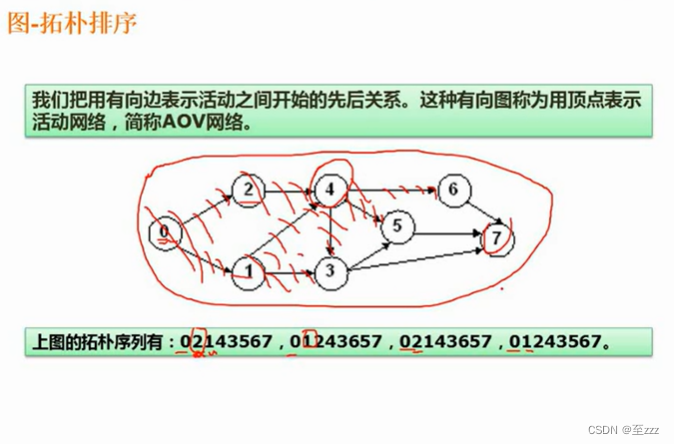
6.4.4 拓扑排序

拓扑排序：用一个序列表达一个图中，哪些事件可以先执行，哪些可以后执行

6.4.5 图的最小生成树(Prim&kruskal)

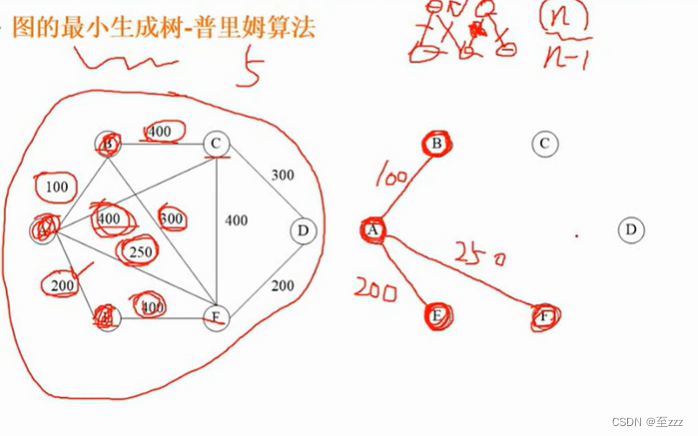
最小生成树：把图的一些边去除，只留下若干条边把所有结点连贯起来，留下的边的权值较小，使得留下来的这部分边的权值加起来最小。求最小生成树有普里姆算法和克鲁斯卡尔算法两种。

• 普里姆算法(Prim)：任选一个结点，将其标为红点集，其余的是蓝点集，然后找出从红点集到蓝点集最短的距离，找出后将其相连，相连的结点纳入红点集，再次寻找红点集到蓝点集最短的距离。选的边不能形成环路。

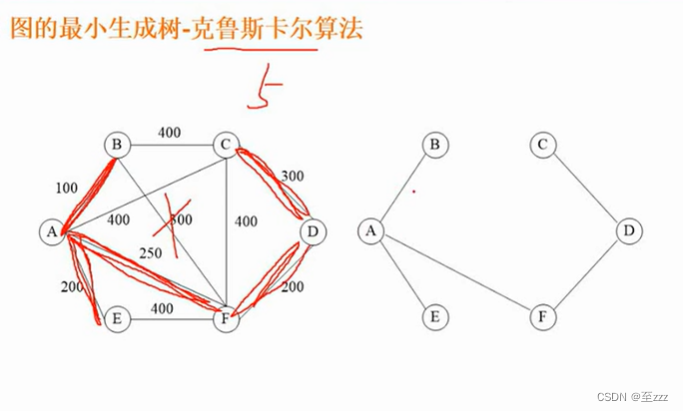
• 克鲁斯卡尔算法(Kruskal)：先确定要选的边的条数（结点数减一），再从整个图中最小的边选起，不能形成环路。

6.5 算法基础

6.5.1 算法的特性

6.5.2 算法的复杂度

时间复杂度：衡量算法执行下来需要耗费多少的时间，时间的量级。
常见的时间复杂度：

• O(1)：执行一条或多条类似于赋值的语句。
• O(log₂n)：在排序二叉树中查询值，其中n为二叉树的层数。二分查找法。
• O(n)：执行一次类似for(i=0;i<n;i++)的语句。
• O(n²)：二层循环嵌套。
• O(n³)：三层循环嵌套。

• 空间复杂度：衡量算法在执行过程中需要使用到的空间或交换空间的数量。

6.6 查找

6.6.1 顺序查找

• 顺序查找：常见、简单但效率较低，时间复杂度为O(n)

6.6.2 二分查找法

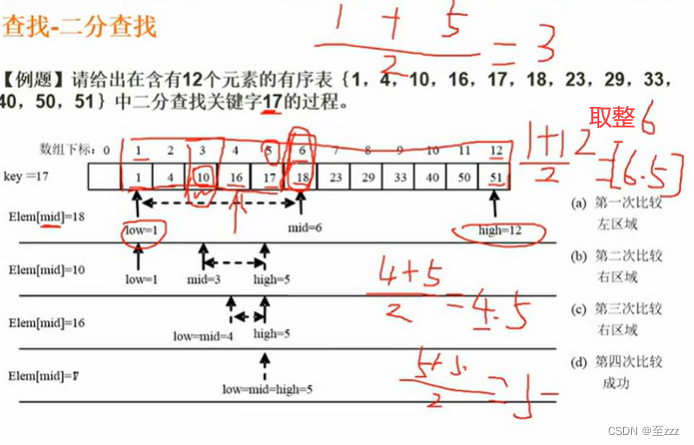
• 二分查找：首先必须是有序序列，查找二叉树就是有这种思想。

注意：比较过的值或区间不再出现在下次比较的区间内。

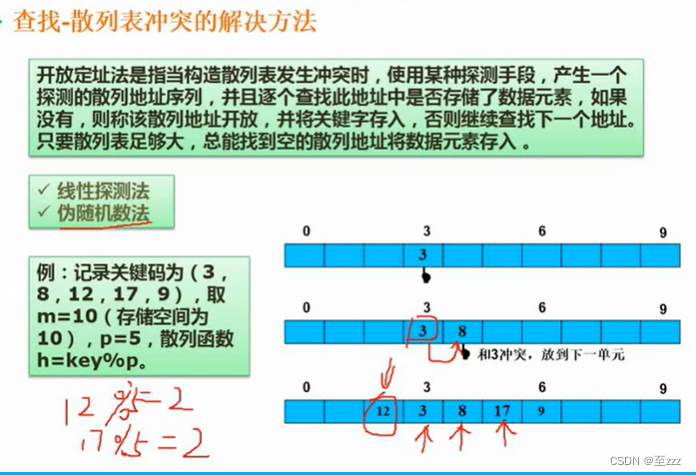
6.6.3 散列表法

类似按内容存储，将数据经过一定的规定运算（散列函数）在存储，若存储时数据冲突，可采用线性探测法和伪随机数法处理。

6.7 排序

6.7.1 基本概念

稳定与不稳定排序 内排序（内存中）与外排序。

• 插入类排序：直接插入排序、希尔排序
• 交换类排序：冒泡排序、快速排序
• 选择类排序：简单选择排序、堆排序
• 归并排序
• 基数排序

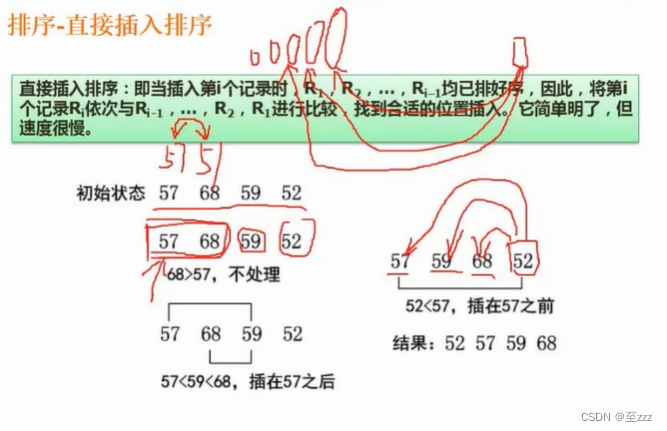
6.7.2 直接插入排序

6.7.3 希尔排序

希尔排序步骤：

• 先取一个增量d1，按照d1位元素间隔将该组元素分为若干个元素组，进行直接插入排序。
• 再取一个增量d2<d1，重复上述操作。
• 直到所取增量d=1。

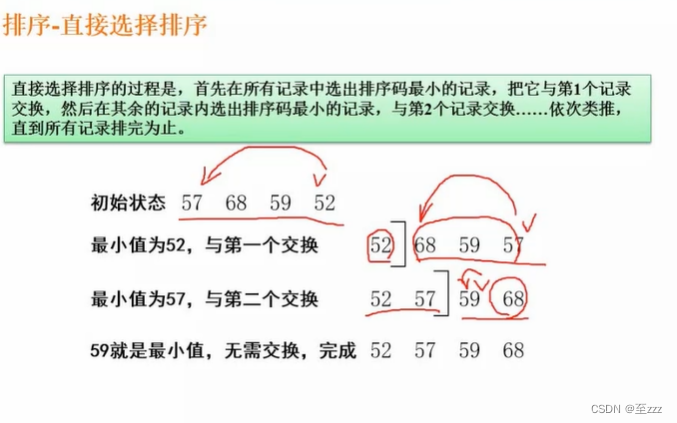
6.7.4 直接选择排序

在未排序的元素组内依次选出最小的元素即可。