Python 数据分析与挖掘（数据探索）

数据探索

1.1 需要掌握的工具（库）

1.1.1 Nump库

1. Numpy 提供多维数组对象和各种派生对象（类矩阵），利用应用程序接口可以实现大量且繁琐的数据运算。可以构建多维数组；提供含有大量对数组数据进行快速运算的数学函数；提供线性代数运算函数；提供随机数生成等功能；提供统计计算功能。
2. ndarray多维数组
   创建ndarray数组
   使用numpy的array（）函数创建
   语法：numpy.array(object,dtype)
   作用：返回满足要求的数组对象。
   说明：
   object：指定生成数组的数据序列，可以是列表、元组。
   dtype： 数据类型，指定数据元素的数据类型 。

1.1.2 Pandas库

1. pandas 提供类似sql的操作（表类似类矩阵），比如增删改查，可以灵活处理缺失值，提供高性能的矩阵运算。
2. Pandas 来源于pandas库中的三种主要数据结构： Panel， DataFrame, Series。
   （1）Series，带标签的一维数组；
   Series 是一个一维的带有标签的数组，这个数据可以由任何类型数据构成，包括整型、浮点、字符、Python 对象等。轴标签被称为「索引」，是 Pandas 最基础的数据结构。
   基本创建方式如下：
   s = pd.Series(data, index=index)
   其中：
   data 可以是 python 对象、numpy 的 ndarray 、一个标量（定值，如 8）
   index 索引是轴上的一个列表，必须和 data 的长度相同，如果没有指定则自动从 0 开始，[0, …, len(data) - 1]
   （2）DataFrame，带标签且大小可变的二维表格结构；
   DataFrame 是 Pandas 定义的一个二维数据结构。横向的称作行（row），一行纵向的称作列（column）。
   第一行是表头，或者可叫字段名，类型 Python 字典里的 key，代码数据的属性。
   第一列是索引（index），就是这行数据所描述的主体，也是这条数据的关键，
   表头和索引在一些场景下也有称列索引和行索引。
   df.loc[ ]只能使用标签索引，不能使用整数索引，通过便签索引切边进行筛选时，前闭后闭。
   df.iloc[]只能使用整数索引，不能使用标签索引，通过整数索引切边进行筛选时，前闭后开。
   （3）Panel，带标签且大小可变的三维数组。
   Pandas 官方中文文档 https://www.pypandas.cn
   盖若 https://www.gairuo.com/p/pandas
   

1.1.3 Matplotlib库（实现可视化）

1. 创建画布与创建子图
   构建出一张空白的画布,并可以选择是否将整个画布划分为多个部分，以便于在同一幅图上绘制多个图形
   当只需要绘制一幅简单图形时，创建子图这部分内容可以省略。
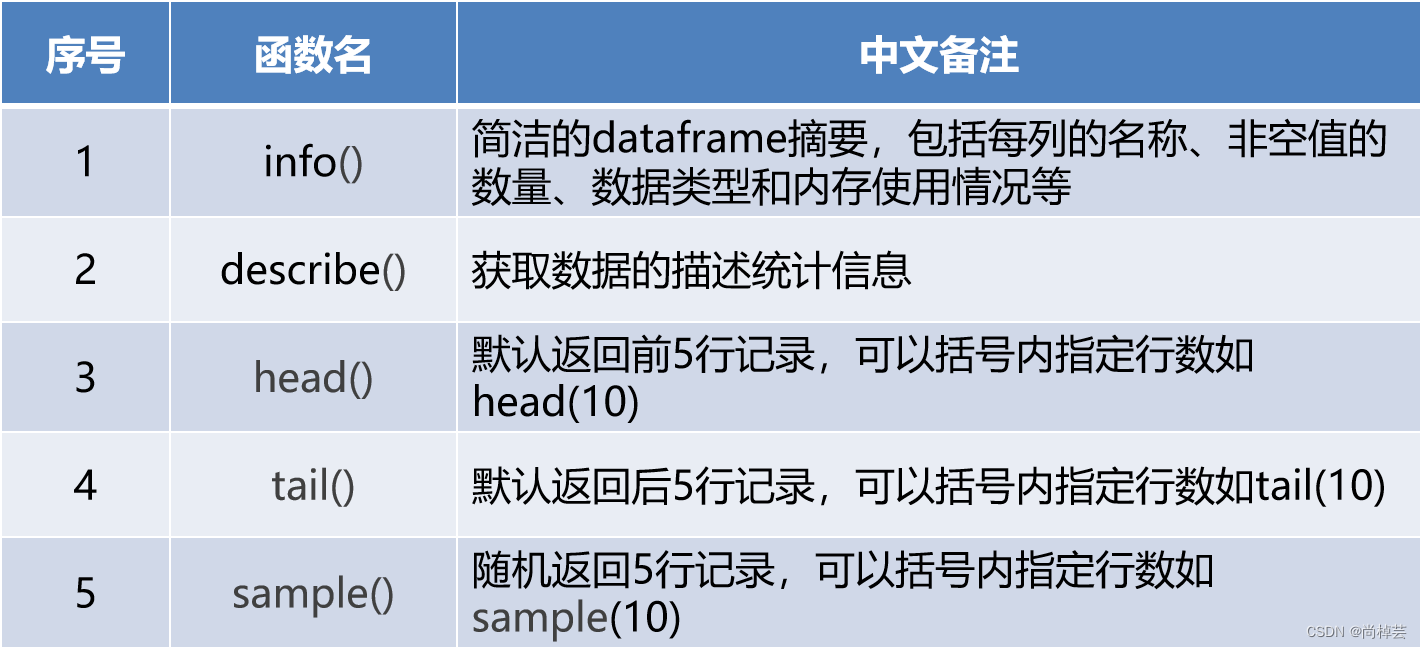
   在pyplot模块中创建画布，创建并选中子图的函数如表所示。
   
2. 添加画布内容
   添加画布内容是绘图的主体部分，其中添加标题、坐标轴名称、绘制图形等步骤是并列的，没有先后顺序，读者可以先绘制图形，也可以先添加各类标签。图例只有在绘制图形之后才可进行添加。
3. 在pyplot模块中添加各类标签和图例的函数如表所示。
   

1.2 数据校验

数据校验可以检查出原始数据中是否存在噪声数据，从而对出现的噪声数据采取相应的解决措施。
噪声数据是指数据中存在着错误或异常，偏离期望值的数据。
数据校验类型包括：一致性检验、缺失值校验、异常值校验。

1.2.1 一致性校验

（1）时间校验
范围不一致，统计区间不同
粒度不一致，采集频率不同
格式不一致，大多来自不同系统
（2）字段信息校验
收集收集过程中，出现重复收集数据或重复写入数据，导致数据冗余。
由于存在重复值，可能存在以下3种情况
同名异义：名称相同，含义不一致
异名同义：名称不同，代表的含义一样
单位不一致：如A系统的单位元，B系统万元

1.2.2 缺失值

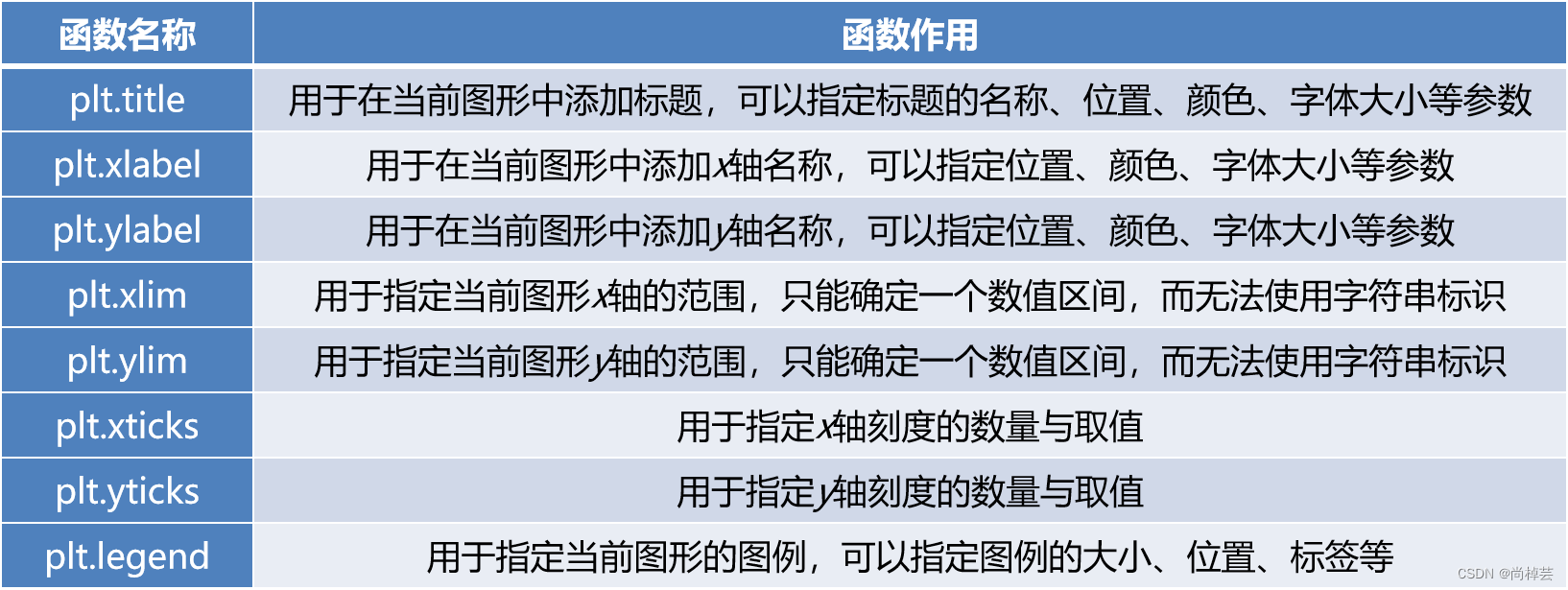
（1）简单统计分析
统计缺失值的属性个数以及每个属性的未缺失数、缺失数、缺失率
panadas 函数：info、describe、isnull().sum()、isnull().any（）
（2）缺失值处理
删除、插补、不处理

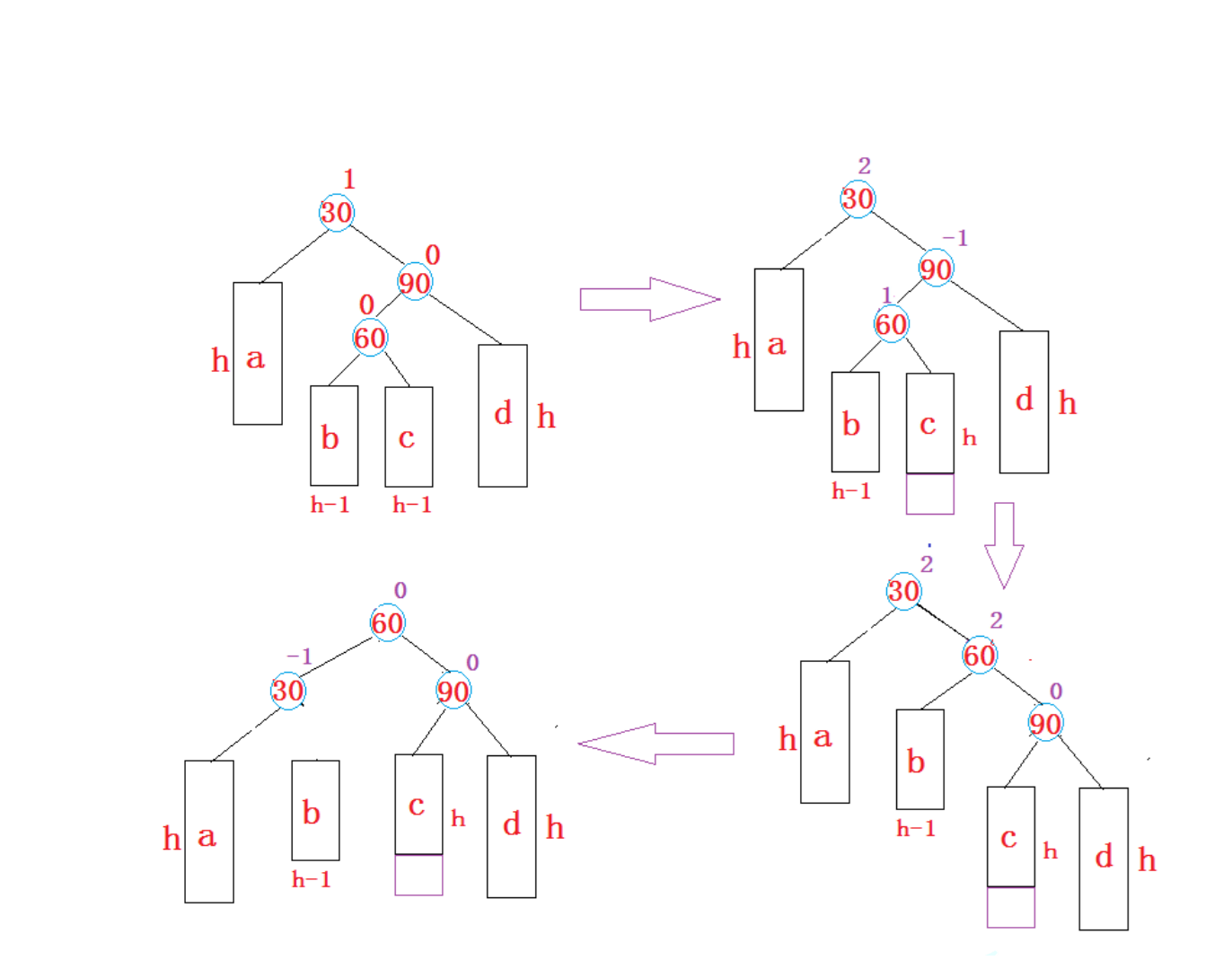
1.2.2 异常值校验

1. （1）目的：是检验数据是否有录入错误以及含有不合常理的数据。
   （2）概念：异常值是指样本中的个别值，其数值明显偏离其余的观测值。异常值也称为离群点，异常值的分析也称为离群点的分析。
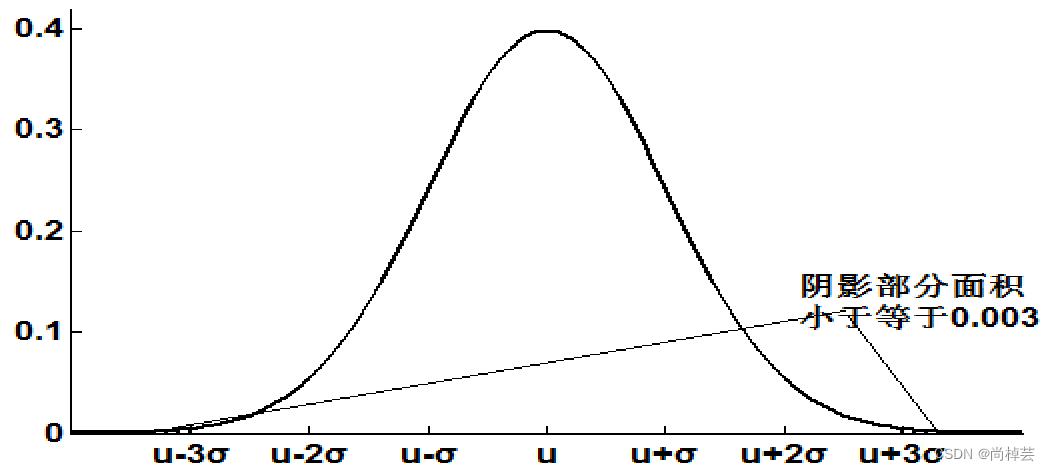
   （3）异常值分析方法主要有：简单统计量分析、3σ原则、箱型图分析。
2. 如果数据服从正态分布，在3σ原则下，异常值被定义为一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下，距离平均值 3σ之外的值出现的概率为P(|x-μ|>3σ) ≦0.003，属于极个别的小概率事件。
   
3. （1）不需要事先假定数据服从特定分布形式，没有对数据作限制性要求。
   （2）箱形图判断异常值的标准以四分位数和四分位距为基础
   （3）四分位数具有一定的鲁棒性：多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响。
   （4）箱形图识别异常值的结果比较客观，有一定优越性。
   
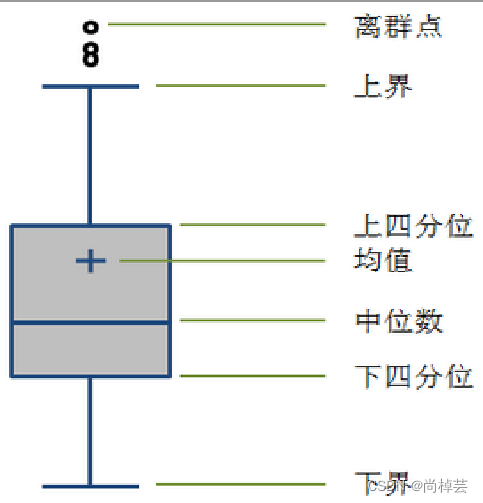
   四分位数（Quantile）：把数据分布划分成4个相等的部分，使得每部分表示数据分布的四分之一。这3个数据点称为四分位数
   
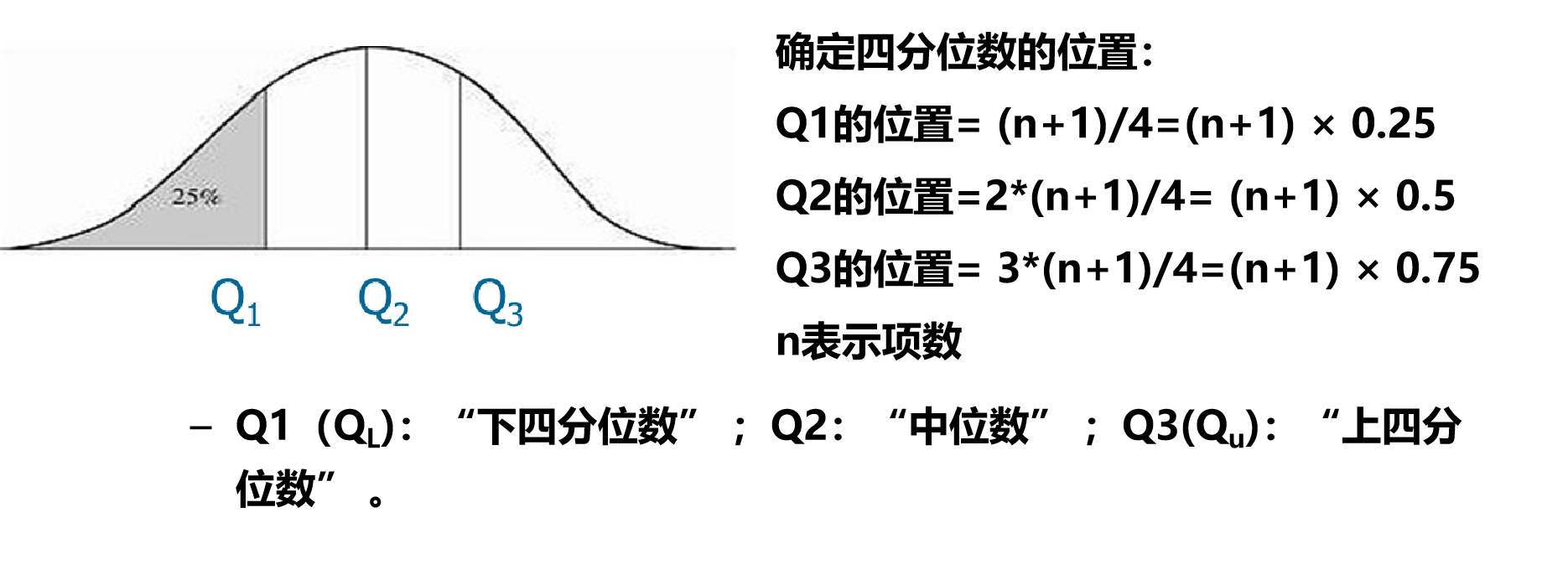
   四分位的计算方式有（n+1)* p，1+（n-1) * p
   两种方式，p分别为0.25，0.5，0.75
   QL=1+(n-1)/4
   QU=1+3*(n-1)/4

1.3 特征分析

1.3.1分布分析

分布分析能揭示数据的分布特征和分布类型，便于发现某些特大或特小的可疑值。
（1）对于定量数据，欲了解其分布形式，是对称的、还是非对称的，可做出频率分布表、绘制频率分布直方图、绘制茎叶图进行直观地分析；直方图有利于分析数据的整体分布情况
（2）对于定性分类数据，可用饼图和条形图直观地显示数据分布情况。
（3）对于定量变量而言，做频率分布分析时选择“组数”是主要的问题，一般按照以下步骤：
求极差（最大值-最小值）
决定组距与组数，组距=极差/组数
决定分布区间
列出频率分布表
绘制频率分布直方图
直方图绘制：（常用结构）
plt.hist（数据，bins=分箱数,density=密度或频数，布尔）
plt.xlabel(‘XXX’,fontsize=15) #x轴标签，字体
plt.ylabel(‘XXX’,fontsize=15,color=‘r’)
plt.title(‘XXX’,fontsize=15)#标题字体
plt.xticks(fontsize=15) #x刻度

g=df.列名.plot.hist(bins=8,grid=True,fontsize=15)
g.set_xlabel(‘XXX’,fontsize=15)
g.set_ylabel(‘XXX’,fontsize=15)
g.set_title(‘XXX’,fontsize=15)
（4）对于定性变量，常常根据变量的分类类型来分组，可以采用饼图和条形图来描述定性变量的分布。
（5）饼图的每一个扇形部分代表每一类型的百分比或频数，根据定性变量的类型数目将饼图分成几个部分，每一部分的大小与每一类型的频数成正比；条形图的高度代表每一类型的百分比或频数，条形图的宽度没有意义。

1.3.2 对比分析

（1）对比分析是指把两个相互联系的指标数据进行比较，从数量上展示和说明研究对象规模的大小，水平的高低，速度的快慢，以及各种关系是否协调。
对比分析主要有以下两种形式：
第一种:绝对数比较（利用绝对数进行对比）
第二种:相对数比较
由两个有联系的指标对比计算的，用以反映客观现象之间数量联系程度的综合指标，其数值表现为相对数。
1)结构相对数 4)强度相对数
2)比例相对数 5)计划完成程度相对数
3)比较相对数 6)动态相对数

1.3.3统计量分析

(1) 用统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析。
(2)平均水平的指标是对个体集中趋势的度量，使用最广泛的是均值和中位数；反映变异程度的指标则是对个体离开平均水平的度量，使用较广泛是标准差（方差）、四分位间距。
集中趋势度量主要有：均值、中位数、众数、中列数。
离中趋势度量主要有：极差、标准差、方差。



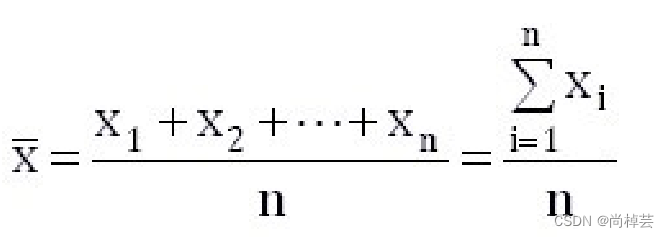
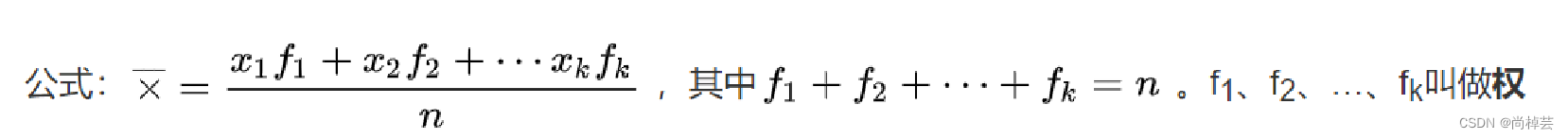
（3）极差： 等于最大值-最小值
标准差：标准差也被称为标准偏差，在概率统计中最常使用作为统计分布程度上的测量依据。标准差是方差的算术平方根。标准差可度量数据偏离均值的程度。d.std()

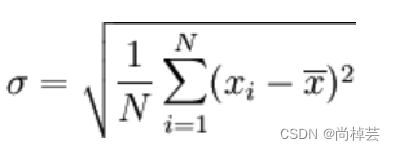
（4）方差：d.var()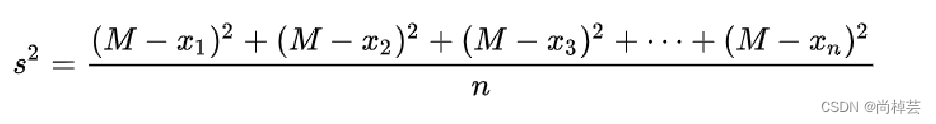

(5)变异系数：又称离散系数。度量标准差相对于均值的离中趋势。
计算公式变异系数=标准差÷均值*100%
主要用来比较2个或多个不同单位或不同波动幅度的数据集的离中趋势。

1.3.4 周期性分析

(1)周期性分析是探索某个变量是否随着时间变化而呈现出某种周期变化趋势。
(2)周期性趋势相对较长的有年度周期性趋势、季节性周期趋势，相对较短的一般有月度周期性趋势、周度周期性趋势，甚至更短的天、小时周期性趋势。
(3)以某景区2019年3月份人流量为例，根据人流量数据，制时序图，并分析景区人流量的变化趋势。

1.3.5贡献度分析

(1) 贡献度分析又称帕累托分析，帕累托法则又称20/80定律。同样的投入放在不同的地方会产生不同的效益。
(2)比如对一个公司来讲，80%的利润常常来自于20%最畅销的产品；而其他80%的产品只产生了20%的利润。
(3)贡献度分析要求我们抓住问题的重点，找到那最有效的20%的热销产品、渠道或者销售人员，在最有效的20%上投入更多资源，尽量减少浪费在80%低效的地方。

1.3.6相关性分析

（1）研究变量之间的关系：了解不同变量之间的相关性强弱和方向。
（2）预测模型建立：在构建预测模型之前，相关性分析可以帮助筛选出对预测目标具有重要影响的变量，从而提高模型的准确性和可解释性。
探索数据集特征：通过分析变量之间的相关性，可以揭示出可能存在的潜在关联。
（3）排除冗余变量：在某些情况下，数据集中可能存在冗余变量，即变量之间存在高度相关性。通过相关性分析，可以鉴别出冗余变量，从而在建模或分析过程中减少冗余信息，提高效率。
（4）分析连续变量之间线性的相关程度的强弱，并用适当的统计指标表示出来的过程称为相关分析。
（5）相关性不等于因果性，也不是简单的个性化，相关性在不同的学科里面的定义也有很大的差异。
（6）相关性分析方法主要有：
直接绘制散点图
绘制散点图矩阵
计算相关系数
（7）函数关系（一一对应关系）
设有两个变量 x 和 y ，变量 y 随变量 x 一起变化，并完全依赖于 x ，当变量 x 取某个数值时， y 依确定的关系取相应的值，则称 y 是 x 的函数，记为 y = f (x)，其中 x 称为自变量，y 称为因变量
某种商品的销售额(y)与销售量(x)之间的关系可表示为 y = p x (p 为单价)
（8）相关性
线性相关——散点图接近一条直线
非线性相关——散点图接近一条曲线
正相关——变量同方向变化，同增同减
负相关——变量反方向变化 ， 一增一减
（9）
为了更加准确的描述变量之间的线性相关程度，可以通过计算相关系数来进行相关分析。在二元变量的相关分析过程中比较常用
Pearson相关系数（皮尔森）
Spearman秩相关系数（斯皮尔曼）
判定系数（相关系数的平方）
（10） 需要同时考察多个变量间的相关关系时，若一一绘制它们间的简单散点图，十分麻烦。此时可利用散点图矩阵来同时绘制各自变量间的散点图，这样可以快速发现多个变量间的主要相关性，这一点在进行多元线性回归时显得尤为重要。
import numpy as np,pandas as pd
v1 = np.random.normal(0, 1, 100)
v2 = np.random.randint(0, 23, 100)
v3 = v1 * v2
df = pd.DataFrame([v1, v2, v3]).T
pd.plotting.scatter_matrix(df)
plt.show()

数据探索实验一

实验1 数据特征分析

一、实验课时
4课时 验证性
二、实验目的
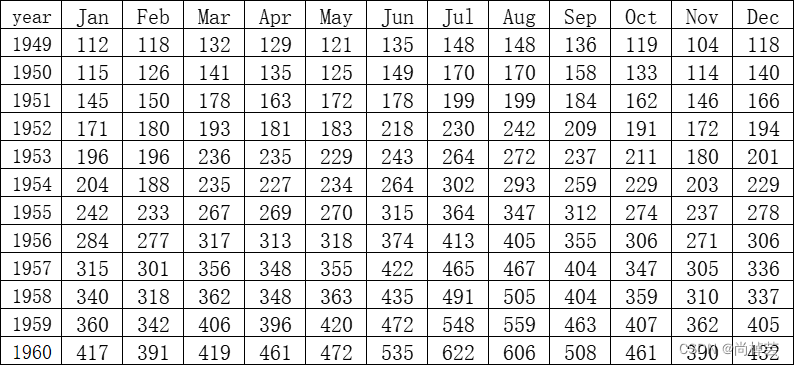
1、根据提供的数据，对航空公司1949-1960年乘客人数做简单的描述性分析。
2、掌握频数分布、集中和离散趋势、偏度和峰度、基本统计图表。
三、实验内容
1、根据数据集找出这12年来客运人数的趋势
2、找出乘客人数的季节趋势
3、对乘客人数做简单的描述性分析。
四、实验流程
1、读取“base.xlsx”excel数据，查看数据信息
使用Pandas对数据excel数据进行获取，并能够查看完整的数据。
问题：对获取到的数据进行一个简单的描述。
2、数据异常值检测1（describe方法）。
3、数据异常值检测2（箱型图），只显示12个月数据，并简单说明分析结果。
4、整理数据
将year作为行索引。
5、乘客数量对比分析
（1）绘制频数分布直方图，查看其中规律。
①按年份进行求和
②按月份进行求和
③使用matplotlib中的条形图对比每年乘客数量，并对分布结果进行分析。
④使用折线图作出每年乘客变化趋势图，并作出分析结果。
⑤对比月度乘客总数量，分析出12个月当中乘客人数的高峰期。
6、对所有的乘客人数做描述性统计
①以年份维度作堆叠得出堆叠结果。
②使用函数生成描述性统计，说明数据集的最大值、最小值、平均值。
③计算出该数据的偏度系数，并根据系数作出分析。
④计算出该数据的峰度系数，并根据系数作出分析。
⑤使用帕累托图表达出航空乘客数量与年份的关系，并标注关键节点数据。
⑥对航空乘客数量进行周期性分析。
五、实验成果要求
1、完成每一项任务
base的表格内容：

代码如下：

import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel("C:\\Users\\86182\\Desktop\\base.xlsx")
data1 = data.iloc[:, 1:12]
plt.rcParams['font.sans-serif'] = ['SimHei']  # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号
data1.boxplot()
plt.title("客运人数异常值检测")
plt.xlabel('月份')#x轴显示月份
plt.ylabel("客运人数（万人）")#y轴显示人数
data2 = data.set_index("year")
data_sum1 = data2.sum(axis=1)  # 按行求和
data_sum2 = data2.sum(axis=0)  # 按列求和
# 分析对比图
plt.figure()  # 绘制画布
plt.title("每年客运人数对比")  # 柱形图题目
plt.xlabel("年份")  # x刻度轴名字
plt.ylabel('人数（万）')  # y刻度轴名字
plt.bar(data['year'], data_sum1)  # 绘制柱形图
for i in range(len(data_sum1)):  # 将柱形图添加具体数值plt.text(data.year[i]-0.4, data_sum1.iloc[i]+0.4, '%.0f'%data_sum1.iloc[i])
# 折线图——每年乘客变化趋势
plt.figure()
plt.title("每年乘客变化趋势")
plt.xlabel("年份")
plt.ylabel('人数（万）')
plt.plot(data['year'], data_sum1, color='red', marker='o')
print(data_sum2.sort_values())  # 返回排序后的月度乘客总量
data3 = data2.stack()
print(data3)
print(data3.describe())
s = pd.Series(data3)
bias_value = s.skew()
peak_value = s.kurt()
print('偏度：', bias_value)
print('峰度：', peak_value)
# 频数分布直方图
plt.figure()data_pingshu = pd.concat([data['Jan'], data['Feb'], data['Mar'], data['Apr'], data['May'], data['Jun'], data['Jul'],data['Aug'], data['Sep'], data['Oct'], data['Nov'], data['Dec']])
bins = [100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650]
plt.hist(data_pingshu, bins, range(100, 650), edgecolor='black')
plt.xticks(bins)
plt.title("频数分布直方图")
# 贡献度分析
plt.figure()
data['headcount'] = data.sum(1)
data4 = data.iloc[:, [0, -1]]
data4 = data4.sort_values(by=['headcount'], ascending=False).reset_index()
data4['headcount'].plot(kind='bar')
print(data4)
plt.ylabel('客运人数（万）')
p = data4['headcount'].cumsum() / data4['headcount'].sum()
print(p)
p.plot(secondary_y=True, style='-o', linewidth=2, color='r')
plt.xticks(range(12), data['year'])
plt.annotate(format(p[8],".2%"), xy=(8, p[8]),xytext=(8*1.2, p[8]*1.2), arrowprops=dict(arrowstyle='->', connectionstyle="arc3"))
plt.ylabel("贡献度比例")
# 周期性分析
plt.figure()
plt.plot(range(144), data3)
plt.xticks(range(0,144,12),data4['headcount'])
plt.title('贡献度分析')
plt.xlabel('年份')
plt.ylabel('人流量')
plt.show()

总结

静中争，稳中急。