EQ 均衡器

EQ 的全称是 Equalizer，EQ 是 Equalizer 的前两个字母，中文名字叫做“均衡器”。最早是用来提升电话信号在长距离的传输中损失的高频，由此得到一个各频带相对平衡的结果，它让各个频带的声音得到了均衡。

EQ 的主要功能是：通过多个滤波器对声音某一个或多个频段进行增益或衰减处理。

滤波器的种类

EQ的种类繁多，但是基本原理都是滤波器的叠加。根据参数的种类可以分为：图示均衡器和参数均衡器。根据滤波器设计又有很多EQ的设计种类：

低通滤波器（lowpass）：简单的处理低频效果，允许某部分低频率经过；没有增益效果。
高通滤波器（highpass）：简单的梳理高频效果，允许某部分高频率部分经过；没有增益效果。
全通滤波器（allpass）：稳定系统响应，使得声音浑浊。
带通滤波器（bandpass）：允许一定频率内通过。
带阻滤波器（bandstop）：使得一定频率被压制。
低切滤波器（Low Shelf）：切断中心频率以下的频率：可调节增益。
高切滤波器（High Shelf）：切断中心频率以上的频率：可调节增益。
峰值滤波器（Peak Filter）：拉高中心频率增益和频率响应。
陷波滤波器（Notch Filter）：压制中心频率的增益和频率响应。

对于low Shelf和Low pass的区别可以参照网站。

图示均衡器（Graphic Equalizer）

下图是Audition设计图示均衡器，该均衡器有10个频段，每个频段增益为-20dB~20dB。利用Audition中的参数滤波器得到一组EQ参数，然后将其应用到尖峰滤波器（peaking filter）

但是图示均衡器有一个缺点，它只能改变固定频带的音量，假如我们想改变1.5kHz处的音量，就没有办法了，因为它只提供了调整1kHz和2kHz的推子。

参数均衡器

参数均衡器主要使用的是峰值滤波器，峰值滤波器在中心频率附近提供提升或削减。远离升压或削减的增益是统一的，因此可以方便地将多个这样的部分串联起来。峰值滤波器的主要参数

采样率$Fs$
中心频率$Fc$：进行滤波的中心点，也即提升或者衰减频段的峰点或谷点所对应的频率
增益（gain/dB）：中心频率处的增益。增益表示输出与输入之比，$Gain=10*log(Out/In)$
品质因子Q：定义滤波器影响的频率范围，描述了某一频率点提升或衰减的频带带宽。以频点为中心，Q 值越大，受影响的频带就越窄，Q 值越小，受影响的频带就越宽。中心频率变化3dB的频率差定义为Q值对应的频带带宽。举例而言，假设信号的中心频率设置为100Hz，对其施加EQ之后，该信号从原幅度衰减了3dB的整个信号被影响的频率范围是95Hz~105Hz，则受影响的频带带宽为10Hz。$Q=\frac{100}{10}=10$

上下限频率$f_1,f_2$：如果是特定的滤波器，一般指频率响应强度下降到-3DB处的频率

Audition有参数均衡器功能，这种 EQ 可以随意定义频点的频率，在写有Hz数的地方输入不同的数值，再输入更改的dB数（分贝），就能改变这个频率的音量。

滤波器的设计

数字滤波器的设计类型：

无限冲激响应（Infinite Impulse Response，IIR）：计算量小，实时性好。

IIR是一种适用于许多线性时不变系统的属性，这些系统的特征是具有一个冲激响应$h(t)$，$h(t)$不会在特定点上完全变为零，而是无限期地持续。

有限冲激响应（Finite Impulse Response，FIR）：稳定性好，相位可控。

在有限冲激响应（FIR）系统中，对于某个有限T，在时t>T时，冲激响应恰好变为零。

多滤波系统设计类型：

级联型：将多个滤波器一个接着一个连接在一起，上一个滤波器的输出作为下一个滤波器的输入，类似于串联。
并联型：各个滤波器并行处理，最后才将结果合并在一起。

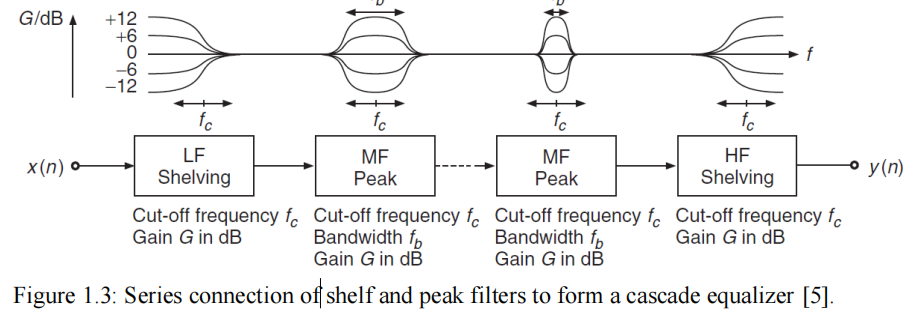
我们选择二阶的biquad(IIR)设计滤波器，biquad响应函数如下：

$$H(z)=\frac{b_0+b_1 z^{-1}+b_2 z^{-2}}{a_0+a_1 z^{-1}+a_2 z^{-2}}$$

上下同时除以$a_0$，对$a_0$进行归一化

$$ H(z)=\frac{Y(z)}{X(z)}=\frac{b_0+b_1 \cdot z^{-1}+b_2 \cdot z^{-2}}{1+a_1 \cdot z^{-1}+a_2 \cdot z^{-2}} $$

转换到时域上差分方程计算方法：

$$y(n)=b_0 \cdot x(n)+b_1 \cdot x(n-1)+b_2 \cdot x(n-2)-a_1 \cdot y(n-1)-a_2 \cdot y(n-2)$$

设计滤波器必要参数

Fs：采样频率
f0：中心频率或角频率或架中点频率，取决于哪种过滤器类型
dBgain：仅用于峰值和倾斜滤波器
Q：对定义进行了调整，以便在相同Q和f0/Fs的情况下提高N dB，然后减少N dB，从而产生精确平坦的单位增益滤波器
BW：以倍频程为单位的带宽（BPF 的 -3 dB 频率之间）和陷波或中点 (dBgain/2) 增益频率之间峰值均衡器
S："搁架斜率"参数（仅适用于搁置均衡器）。当S=1时，陆架坡度尽可能陡并保持单调随着频率的增加或减少增益。陆架坡度，在dB/倍频程，对于 a 的所有其他值仍与 S 成比例固定 f0/Fs 和 dBgain。

然后计算几个中间变量：

$A = \sqrt{10^{dBgain/20}}= 10^{dBgain/40}$ (for peaking and shelving EQ filters only)

$w0 = 2*pi*f0/Fs$

cos(w0)
sin(w0)

alpha = sin(w0)/(2*Q) (case: Q)
　　 = sin(w0)*sinh( ln(2)/2 * BW * w0/sin(w0) ) (case: BW)
　　 = sin(w0)/2 * sqrt( (A + 1/A)*(1/S - 1) + 2 ) (case: S)

供参考: 带宽与Q的关系为

带BLT的数字滤波器：$1/Q = 2*sinh(ln(2)/2*BW*w0/sin(w0))$
模拟滤波器原型：$1/Q = 2*sinh(ln(2)/2*BW)$

shelf slope 与Q的关系为：$1/Q = sqrt((A + 1/A)*(1/S - 1) + 2)$

$2*sqrt(A)*alpha = sin(w0) * sqrt( (A^2 + 1)*(1/S - 1) + 2*A ) $是一个方便的中间变量，用于shelf EQ滤波器。

最后，计算每种滤波器的系数，以及对应的模拟滤波器原型 H(s)：

低通滤波器

LPF：$H(s) = 1 / (s^2 + s/Q + 1)$

b0 = (1 - cos(w0))/2

b1 = 1 - cos(w0)

b2 = (1 - cos(w0))/2

a0 = 1 + alpha

a1 = -2*cos(w0)

a2 = 1 - alpha

高通滤波器(High Pass Filter)

HPF：$H(s) = s^2 / (s^2 + s/Q + 1)$

b0 = (1 + cos(w0))/2

b1 = -(1 + cos(w0))

b2 = (1 + cos(w0))/2

a0 = 1 + alpha

a1 = -2*cos(w0)

a2 = 1 - alpha

带通滤波器(增益 = Q )

BPF：$H(s) = s / (s^2 + s/Q + 1)$ (constant skirt gain, peak gain = Q)

b0 = sin(w0)/2 = Q*alpha

b1 = 0

b2 = -sin(w0)/2 = -Q*alpha

a0 = 1 + alpha

a1 = -2*cos(w0)

a2 = 1 - alpha

带通滤波器( 0 db增益）

BPF: $H(s) = (s/Q) / (s^2 + s/Q + 1)$ (constant 0 dB peak gain)

b0 = alpha

b1 = 0

b2 = -alpha

a0 = 1 + alpha

a1 = -2*cos(w0)

a2 = 1 - alpha

Notch滤波器

notch: $H(s) = (s^2 + 1) / (s^2 + s/Q + 1)$

b0 = 1

b1 = -2*cos(w0)

b2 = 1

a0 = 1 + alpha

a1 = -2*cos(w0)

a2 = 1 - alpha

全通滤波器

APF: $H(s) = (s^2 - s/Q + 1) / (s^2 + s/Q + 1)$

b0 = 1 - alpha

b1 = -2*cos(w0)

b2 = 1 + alpha

a0 = 1 + alpha

a1 = -2*cos(w0)

a2 = 1 - alpha

峰值滤波器

peakingEQ: $H(s) = (s^2 + s*(A/Q) + 1) / (s^2 + s/(A*Q) + 1)$

b0 = 1 + alpha*A

b1 = -2*cos(w0)

b2 = 1 - alpha*A

a0 = 1 + alpha/A

a1 = -2*cos(w0)

a2 = 1 - alpha/A

低切滤波器

lowShelf: $H(s) = A * (s^2 + (sqrt(A)/Q)*s + A)/(A*s^2 + (sqrt(A)/Q)*s + 1)$

b0 = A*( (A+1) - (A-1)*cos(w0) + 2*sqrt(A)*alpha )

b1 = 2*A*( (A-1) - (A+1)*cos(w0) )

b2 = A*( (A+1) - (A-1)*cos(w0) - 2*sqrt(A)*alpha )

a0 = (A+1) + (A-1)*cos(w0) + 2*sqrt(A)*alpha

a1 = -2*( (A-1) + (A+1)*cos(w0) )

a2 = (A+1) + (A-1)*cos(w0) - 2*sqrt(A)*alpha

高通滤波器

highShelf: $H(s) = A * (A*s^2 + (sqrt(A)/Q)*s + 1)/(s^2 + (sqrt(A)/Q)*s + A)$

b0 = A*( (A+1) + (A-1)*cos(w0) + 2*sqrt(A)*alpha )

b1 = -2*A*( (A-1) + (A+1)*cos(w0) )

b2 = A*( (A+1) + (A-1)*cos(w0) - 2*sqrt(A)*alpha )

a0 = (A+1) - (A-1)*cos(w0) + 2*sqrt(A)*alpha

a1 = 2*( (A-1) - (A+1)*cos(w0) )

a2 = (A+1) - (A-1)*cos(w0) - 2*sqrt(A)*alpha

参见本文代码：PyEqualizer: 用python画出各种类型的EQ频响曲线，并且进行串联滤波。用python画出各种类型的EQ频响曲线，并且进行串联滤波（顺便帮忙点个赞呗）

上述代码需要人工设置中心频率fc，Q值和dBgain，这些参数的调节需要一定的经验，并可借助一些软件如Audition快速方便地获取合适的值。

点击Audition菜单栏的【效果】——【滤波与均衡】——【参数均衡器】，调出参数滤波器。在界面中，可见“频率”（也即中心频率），“增益”和“Q/宽度”，在新版的Audition中还有一栏“频段”，是滤波器标识符。其中【HP】和【LP】，即高通和低通，高通指允许高频通过，滤掉低频信号；低通指允许低频通过，滤掉高频信号。可任意修改【HP】对应的频率，比如设置高通【HP】频率为100Hz，即允许100Hz以上的频率通过，去除100Hz以下噪声；同时可以修改【HP】和【LP】的增益斜率，比如修改增益斜率为24dB/Oct，即低频的曲线斜率为24dB/Oct（分贝/倍频程）。Au中的EQ处理方法——图形均衡器和参数均衡器

音频频率知识

HF（高频）：6kHz-16kHz，影响音色的表现力、解析力。像音乐盒那种尖锐的声音.

MID HF（中高频）：600Hz-6kHz，影响音色的明亮度、清晰度。像大提琴那种中规中矩的声音.

MID LF（中低频）：200Hz-600Hz，影响音色和力茺和结实度。像大提琴那种中规中矩的声音.

LF（低频）：20Hz-200Hz，影响音色的混厚度和丰满度。像低音炮那种低沉的声音.

人耳可分辨的声音频率大约是在20Hz~20kHz，因此调音台中的四段均衡器把其分为的4个频段，根据德国柏林音乐研究所资料介绍，它们是：

31Hz——这个频段需要播放器材有比较好的低频下潜能力，如果没有，当然就不容易听见，这个频段主要影响底鼓的延续音（sustain)，就是踩下底鼓之后嗡嗡的声音，增强这个频段可以让音乐浑厚。

63Hz——这个频段是底鼓所在的主要频段，如果单纯把这个频点增强10dB，最明显的感受就是底鼓声变得很大，甚至破了，所以增强这个频段有助于音乐更厚实。

125Hz——这就主要是贝斯的频段了，贝斯常用的音高位置的音色主要在这一频段，当然不是说这一频段只有贝斯，增强这一频段音乐会更扎实。

基本上，如果增强了上述三个频段，你想要重低音的话就有了，这里说一下遮蔽效应，简单说就是比如你把125Hz调的很大，那么靠近125Hz的、dB数小的频率就会被遮蔽，听不到了。

250Hz——这个频段多了声音会很脏，少了声音会很干净，硬实，但它同时也是人声、弦乐、手鼓等等音色的主要共鸣点的所在频段。可以想象在水下的那种轰隆隆的感觉，是这一频段带给我的主要感受。

500Hz——和250Hz的感受相似，这一频段的增强会使一些铺底的合成器pad音色凸显出来，会使更多的男声凸显出来，这一频段多了还是会浑浊，稍微增加一些会使音乐有更多温暖、亲近的感觉。

1000Hz——这个频段可以算作一个分水岭，大部分乐器的基频都在200—1000Hz，所以调节1000以下的频段会更多的影响音色（不是影响音量），增强这一频段会使音色更明亮。

2000Hz——增强人声的可懂性，说白了听得更清楚，包括吉他贝斯的琴弦摩擦的声音，电吉他的尖刺感，两元店大喇叭里的广告，都可以让你更多的体会这一频段的特点，所以增强这一频段让音乐更清晰。

4000Hz——我个人理解这一频段是很多音色的镶边，就像是相框的边框，衣服或者窗帘的下摆，很多时候这一频段可以让声音更完整，更具细节，更多现场感，但是过多的提升也会让人觉得刺耳，听觉疲劳。5000Hz以上是几乎所有乐器的谐波成分，也是人耳最敏感的频段，比如把5000Hz提升6dB，有时会让人觉得整个音量被开大了一倍，如果过多的衰减则会让音乐听起来很远。

8000Hz——这个频段比较明显的是各种镲声、弦乐摩擦琴弦的声音、还有就是齿音，比如提升该频段会放大歌手四、是、次、字一类的发音。一般很少会大幅提升这一频段。

16000Hz——事实上这一频段确实很难分辨，如果把一首歌的16000Hz提升10dB，我一般会去听各种镲，镲会显得更亮更大声了，反之，镲声会显得小了、暗了。如果不仔细听，会感觉音乐没什么变化。