课程1_第2周_测验题

目录：目录

第一题

1.神经元计算什么？

A. 【  】神经元计算激活函数后，再计算线性函数（z=Wx+b）

B. 【  】神经元计算一个线性函数（z=Wx+b），然后接一个激活函数

C. 【  】神经元计算一个函数g，它线性地缩放输入x（Wx+b）

D. 【  】神经元先计算所有特征的平均值，然后将激活函数应用于输出

答案：

B.【 √ 】神经元计算一个线性函数（z=Wx+b），然后接一个激活函数

第二题

2.以下哪一个是逻辑回归的损失函数？

A. 【  】$L^{(i)}({\hat{y}}^{(i)},y^{(i)})=|y^{(i)}-{\hat{y}}^{(i)}|$

B. 【  】$L^{(i)}({\hat{y}}^{(i)},y^{(i)})=max(0,y^{(i)}-{\hat{y}}^{(i)})$

C. 【  】$L^{(i)}({\hat{y}}^{(i)},y^{(i)})=|y^{(i)}-{\hat{y}}^{(i)}{|}^2$

D. 【  】$L^{(i)}({\hat{y}}^{(i)},y^{(i)})=-(y^{(i)}log({\hat{y}}^{(i)})+(1-y^{(i)})log(1-{\hat{y}}^{(i)}))$

答案：

D.【 √ 】$L^{(i)}({\hat{y}}^{(i)},y^{(i)})=-(y^{(i)}log({\hat{y}}^{(i)})+(1-y^{(i)})log(1-{\hat{y}}^{(i)}))$

第三题

3.假设img是一个（32, 32, 3）数组，表示一个32x32图像，它有三个颜色通道：红色、绿色和蓝色。如何将其重塑为列向量？

A. 【  】x = img.reshape((1, 32 * 32, 3))

B. 【  】x = img.reshape((32 * 32 * 3, 1))

C. 【  】x = img.reshape((3, 32 * 32))

D. 【  】x = img.reshape((32 * 32, 3))

答案：

B.【 √ 】x = img.reshape((32 * 32 * 3, 1))

第四题

4.考虑以下两个随机数组a和b：

a = np.random.randn(2, 3) # a.shape = (2, 3)
b = np.random.randn(2, 1) # b.shape = (2, 1)
c = a + b

c的维度是什么？

A. 【  】c.shape = (3, 2)

B. 【  】c.shape = (2, 1)

C. 【  】c.shape = (2, 3)

D. 【  】计算不成立因为这两个矩阵维度不匹配

答案：

C.【 √ 】c.shape = (2, 3)

第五题

5.考虑以下两个随机数组a和b：

a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a * b

c的维度是什么？

A. 【  】c.shape = (4, 3)

B. 【  】c.shape = (3, 3)

C. 【  】c.shape = (4, 2)

D. 【  】计算不成立因为这两个矩阵维度不匹配

答案：

D.【 √ 】计算不成立因为这两个矩阵维度不匹配

Note：运算符 “*” 说明了按元素乘法来相乘，但是元素乘法需要两个矩阵之间的维数相同，所以这将报错，无法计算。

第六题

6.假设每个示例有$n_x$个输入特性，$X=[X^{(1)}，X^{(2)}\dots ,X^{(m)}]$。$X$的维数是多少？

A. 【  】(m, 1)

B. 【  】(1, m)

C. 【  】($n_x$, m)

D. 【  】(m, $n_x$)

答案：

C.【 √ 】($n_x$, m)

第七题

7.np.dot(a，b)对a和b的进行矩阵乘法，而a * b执行元素的乘法，考虑以下两个随机数组a和b：

a = np.random.randn(12288, 150) # a.shape = (12288, 150)
b = np.random.randn(150, 45) # b.shape = (150, 45)
c = np.dot(a, b)

c的维度是什么？

A. 【  】c.shape = (12288, 150)

B. 【  】c.shape = (150, 150)

C. 【  】c.shape = (12288, 45)

D. 【  】计算不成立因为这两个矩阵维度不匹配

答案：

C.【 √ 】c.shape = (12288, 45)

第八题

8.请考虑以下代码段：

#a.shape = (3,4)  
#b.shape = (4,1)  
for i in range(3):  for j in range(4):  c[i][j] = a[i][j] + b[j]

如何将之矢量化？

A. 【  】c = a + d

B. 【  】c = a +b.T

C. 【  】c = a.T + b.T

D. 【  】c = a.T + b

答案：

B.【 √ 】c = a +b.T

Note：a的每一行元素，逐行相加b的每一行元素

第九题

9.请考虑以下代码段：

a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b

c的维度是什么？

A. 【  】这会触发广播机制，b会被复制3次变成(3, 3)，而 * 操作是元素乘法，所以c.shape = (3, 3)

B. 【  】这会触发广播机制，b会被复制3次变成(3, 3)，而 * 操作是矩阵乘法，所以c.shape = (3, 3)

C. 【  】这个操作将一个3x3矩阵乘以一个3x1的向量，所以c.shape = (3, 1)

D. 【  】这个操作会报错，因为你不能用 * 对这两个矩阵进行操作，你应该用np.dot(a, b)

答案：

A.【 √ 】这会触发广播机制，b会被复制3次变成(3,3)，而 * 操作是元素乘法，所以c.shape = (3, 3)

第十题

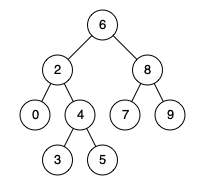
10.请考虑以下计算图：

输出J是？

A. 【  】J = (c - 1) * (b + a)

B. 【  】J = (a - 1) * (b + c)

C. 【  】J = a * b + b * c + a * c

D. 【  】J = (b - 1) * (c + a)

答案：

B.【 √ 】J = (a - 1) * (b + c)