之前经常看到图神经网络的内容,但是一直都觉得很难,就没有继续了解,现在抽空学习了一下,简单了解GNN是个什么东西,还没有进行代码实践,随着后续的学习,会继续更新代码的内容,这里先记录一下,方便以后查阅。
图神经网络 GNN
- 图的基本内容
- 图的基本知识
- 图的基本元素
- 图的表示——邻接矩阵
- 把一些内容表示成图
- 图片表示成图
- 将一句话表示成图
- 分子结构表示成图
- 社会人物关系表示成图
- 图的表示——邻接表
- 图的度和邻居
- 结构特征、节点特征、边特征
- 图的分类
- 图学习的优势
- 图学习的应用
- 节点级别任务
- 边级别任务
- 图级别任务
- 图学习算法的分类
- 图神经网络 GNN
- 什么是GNN
- 图神经网络的目的
- 最简单的GNN层
- 通过池化信息对GNN预测
- Passing messages between parts of the graph
- Learning edge representations
- 加入全局信息
- 多层GNN的作用
- 图卷积神经网络 GCN
- 半监督学习
- GCN的计算
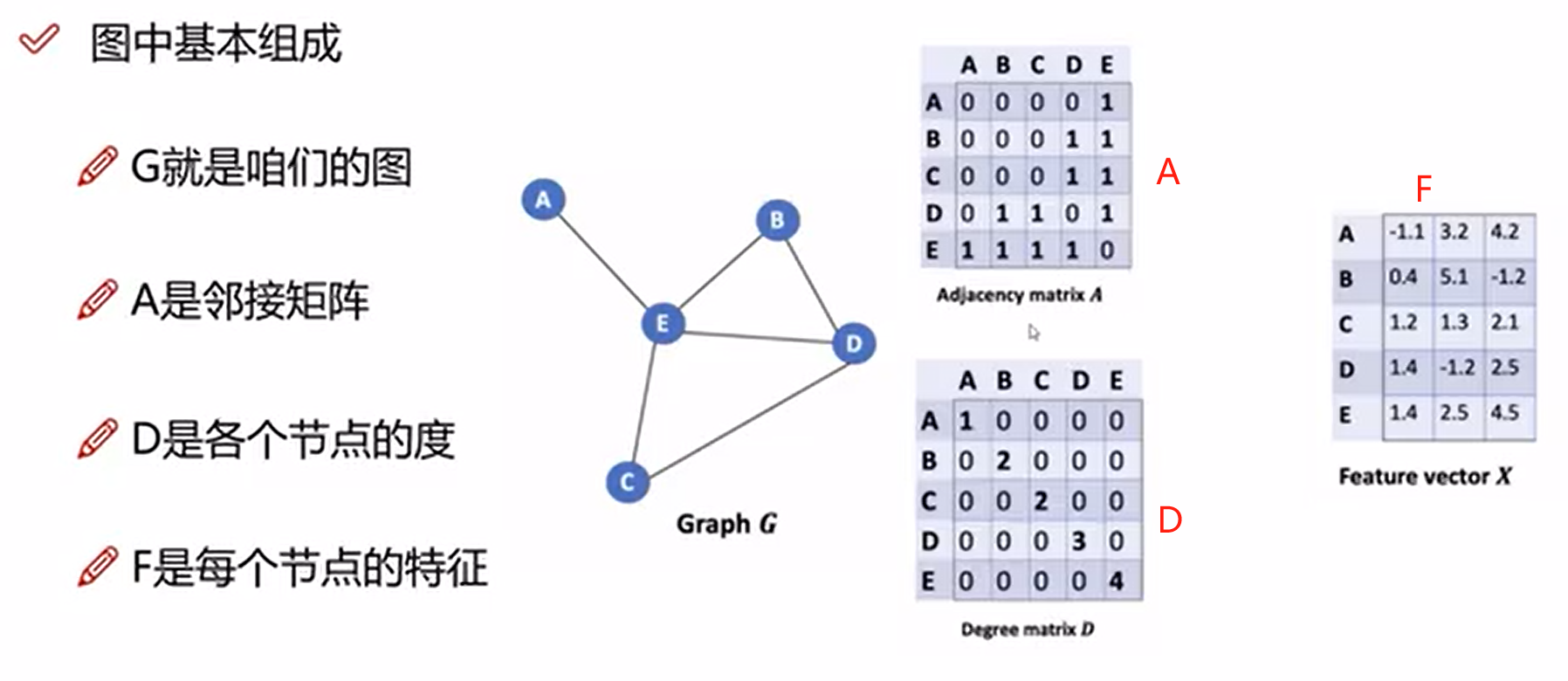
- 图中基本组成
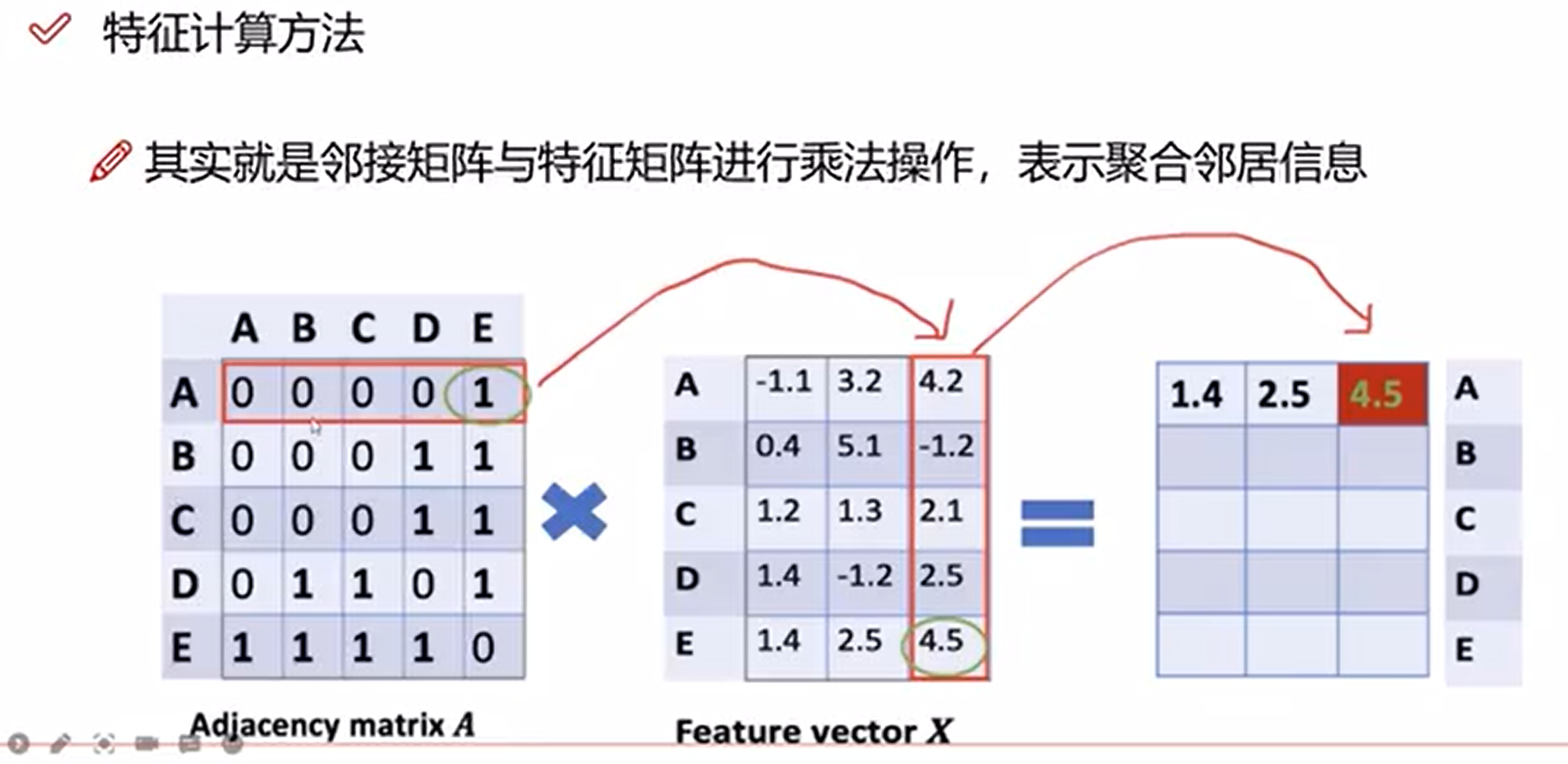
- 特征计算方法
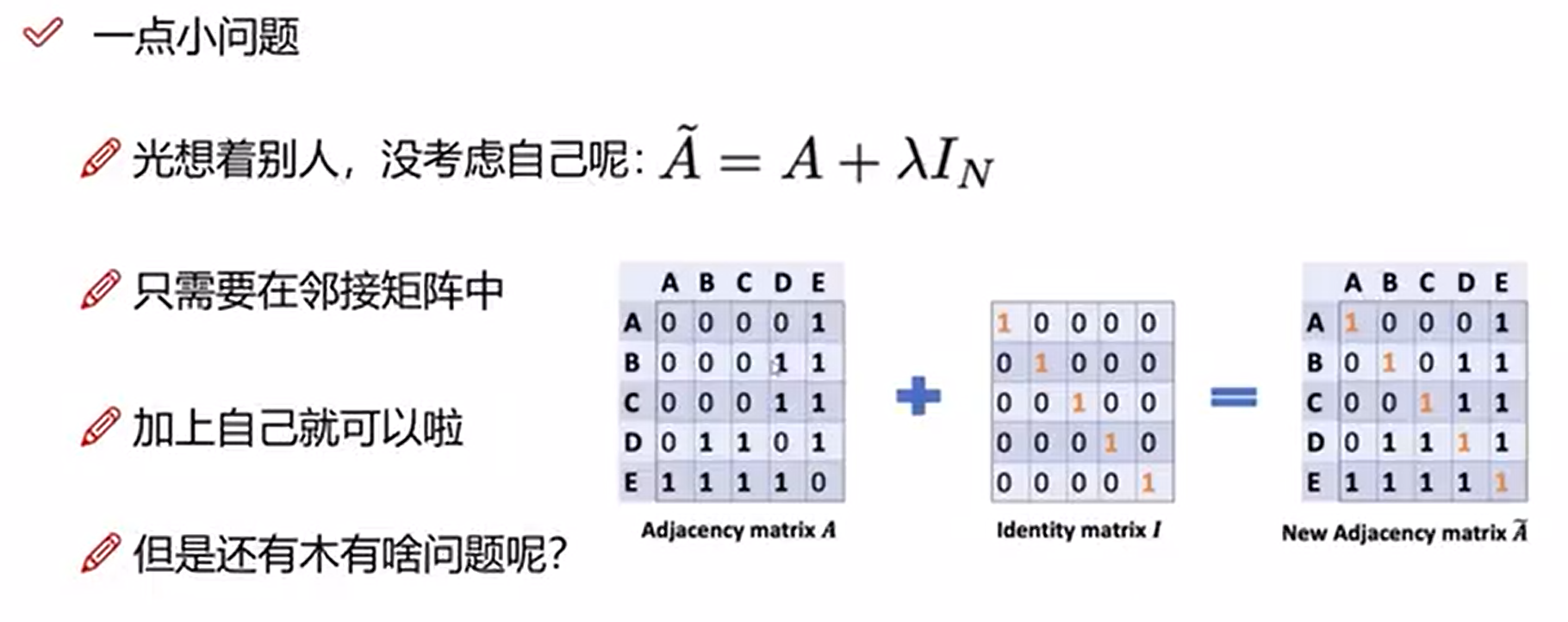
- 邻接矩阵的变换
- GCN层数
- 参考资料
图的基本内容
图的基本知识
图的基本元素
图是由一些点和一些线构成的,能表示一些实体之间的关系,图中的点就是实体,线就是实体间的关系



为了进一步描述每个节点、边或整个图,我们可以在图的每个部分中存储信息

每个顶点、边和整张图都可以用一个向量来表示,在这个例子中,顶点的向量有六个值,柱体的高矮就表示该值的大小,每条边用一个长为8的向量来表示,全局用一个长为5的向量来表示
图的表示——邻接矩阵

把一些内容表示成图
图片表示成图

将一句话表示成图

分子结构表示成图

社会人物关系表示成图

图的表示——邻接表
图上有四种信息:顶点的属性,边的属性,全局信息以及连接性(即为每条边连接的是哪两个顶点)。前三个信息都能用向量来表示,怎么表示连接性呢?
我们可以用邻接矩阵来表示,该矩阵会是一个方阵,但是有一些问题。这个矩阵可能会非常大而且很稀疏,在空间上效率低下,并且计算比较困难。另外将邻接矩阵的行或列的顺序进行交换不会改变其属性的。
比如下面两张图都是前面“Othello"的人物关系图,看着不一样只是因为行和列的顺序不同,但是表示的信息是一样的。这就意味着如果你设计一个神经网络,无论你用下面两张图中的哪一张,都要保证得到的结果是一样的

下面的示例显示了可以描述这个 4 个节点的小图的每个邻接矩阵。

如果既想高效的存储邻接矩阵,又想这个顺序不会影响神经网络的结果,就可以用邻接链表的方式来表示邻接矩阵
比如下方这个,顶点,边和全局信息都用标量来表示,也可以用向量,连接性用邻接链表来表示,邻接链表的数量和边的数量是一致的,第 i i i项表示的是第 i i i条边连接的两个顶点;这样表示就很高效,而且不会受到顺序的影响

图的度和邻居

结构特征、节点特征、边特征

图的分类


图学习的优势


图学习的应用

节点级别任务
前面武术班的例子,假如说两个老师决裂,根据该社交图预测学生会选择哪个老师

金融诈骗检测

目标检测

边级别任务
先给出一张图片,然后经过语义分割将人物给分割出来,然后预测人物间的关系;这个图中顶点已经有了,相当于是预测边的属性

推荐系统

图级别任务
在这个任务中,目标是预测图形的属性,辨别图中是否含有两个环;该任务是分类问题

气味识别

图学习算法的分类

图神经网络 GNN
什么是GNN
A GNN is an optimizable transformation on all attributes of the graph (nodes, edges, global-context) that preserves graph symmetries (permutation invariances).
GNN 是对图的所有属性(节点、边、全局上下文)的可优化变换,可保留图对称性(排列不变性)。
这里的GNN是用“信息传递神经网络”框架来搭建的,GNN的输入是一个图,输出也是一个图,它会对你的图的属性(点,边,全局信息)进行变换,但不会改变图的连接性,就是哪条边连接哪条顶点,这个信息是不会改变的。
无论事情整的多么复杂,我们用图神经网络的目的就是整合特征
图神经网络的目的

最简单的GNN层
对顶点向量、边向量和全局向量分别构造一个多层感知机(MLP),输入的大小和输出的大小是相同的,这三个MLP就组成了一个GNN的层,输入是一个图,输出也是一个图,并且连接性不变。

满足了上文中对GNN的第一个要求,只对属性进行变换,并不改变图的结构;并且MLP是对每个向量独自作用,对样本前后顺序没有要求,所以也就满足了图的排列不变性,满足了第二个要求。
通过池化信息对GNN预测
我们已经构建了一个简单的 GNN,但是我们如何在上面描述的任务进行预测呢?
考虑最简单的情况,例如前面讲到的武术馆的那张社交图。根据那张图来预测学生最终会选择哪个老师,顶点已经用向量来表示,可以直接加一个输出为2的全连接层。

但是,如果顶点中没有信息,信息储存在边中,我们就需要一种收集边信息的方法,将其用作顶点预测。我们可以通过池化来完成这一步。

如果我们只有边特征,并且尝试预测二分类节点信息,我们可以使用池化将信息路由(或传递)到需要去的地方,模型看起来像这样

如果我们只有节点特征,并尝试预测二分类边信息,则模型如下所示

如果我们只有节点级特征,并且需要预测二分类全局属性,则需要将所有可用的节点信息收集在一起并聚合它们。这类似于 CNN 中的全局平均池层。对于边也可以进行同样的操作。

我们可以将最简单的GNN模型总结成如下的结构。
一张图输入,经过GNN层(实质上就是三个分别对应点、边和全局的MLP),输出一个属性已经变换但是连接性不变的图,在经过全连接层,得到输出。

这个结构中,我们没有利用到图各部分之间的连接性,每个部分都是单独处理的,仅仅在池化的时候用了其他部分的信息,下面将告诉大家,怎么来汇集全图信息。
Passing messages between parts of the graph
我们可以在GNN层中使用池化来感知到图形的连通性,做出更复杂的预测。可以通过passing messages来完成,通过消息传递,相邻节点或边缘传递信息并影响彼此的更新。
消息传递分为三步:
-
对于图中的每个节点,收集所有相邻节点嵌入(或消息)。
-
通过聚合函数(如sum)聚合所有消息。
-
所有合并的消息都通过一个更新函数传递,通常是一个学习过的神经网络。

消息传递可以在顶点或边之间发生,这是我们利用图形连结性的关键,我们将在GNN层中构建更详细的消息传递变体,以产生具有增强表现力和力量的GNN模型。
这让人想起标准卷积:本质上,消息传递和卷积是聚合和处理元素邻居信息以更新元素值的操作。在图形中,元素是一个节点,在图像中,元素是一个像素。但是,图中相邻节点的数量可以是可变的,这与图像中每个像素具有固定数量的相邻元素不同。
通过将消息传递GNN层堆叠在一起,节点最终可以合并来自整个图的信息

图中红框表示的是聚合该顶点1近邻的顶点信息,就是聚合距离该顶点为1的顶点信息。
Learning edge representations
我们的数据集并不总是包含所有类型的信息(节点、边和全局上下文)。当我们想要对节点进行预测,但我们的数据集只有边信息时,我们在上面展示了如何使用池化将信息从边传递到节点,但仅限于模型的最终预测步骤。我们可以使用消息传递在 GNN 层内的节点和边之间共享信息。
先把与边连接的顶点信息池化,传递到边上,边通过更新后,再把与顶点相连接的边信息池化传递给顶点,再通过MLP进行更新。如果顶点和边向量的长度不一样,需要先通过投影到相同维度,再做传递。

我们更新哪些图属性以及更新它们的顺序是构建 GNN 时的一项设计决策。我们可以选择是否在边缘嵌入之前更新节点嵌入,或者反之亦然。这是一个开放的研究领域,具有多种解决方案 - 例如,我们可以以“编织”方式进行更新,其中我们有四种更新的表示形式,它们组合成新的节点和边表示形式:节点到节点(线性)、边到边(线性)、节点到边(边层)、边到节点(节点层)。


加入全局信息
我们之前的消息传递,只考虑了1近邻的点,如果一个点想要了解到距离他很远的信息,这是一个问题。为此我们提出master node or context vector,这是一个虚拟的点,他可以和任何其他点或者任何边相连接,这个就是全局信息U。 U是全局信息,它可以和图中的任何信息相连接。
在汇聚顶点信息到边的时候,也会把U一起汇聚,把边信息传递给顶点的时候,也会把U一起传递;然后更新边和顶点后,将边和顶点的信息一起汇聚给U,之后做MLP更新。

在顶点预测中,我们可以用顶点信息、相邻顶点信息、连接边信息、全局信息中的全部或者选择其中几项,来更新顶点信息,做顶点预测;这些信息可以简单地加在一起,也可以通过其他方式汇聚在一起。

多层GNN的作用
层数越多,GNN的“感受野”越大,每个点考虑其他点的信息越多,考虑越全面

图卷积神经网络 GCN
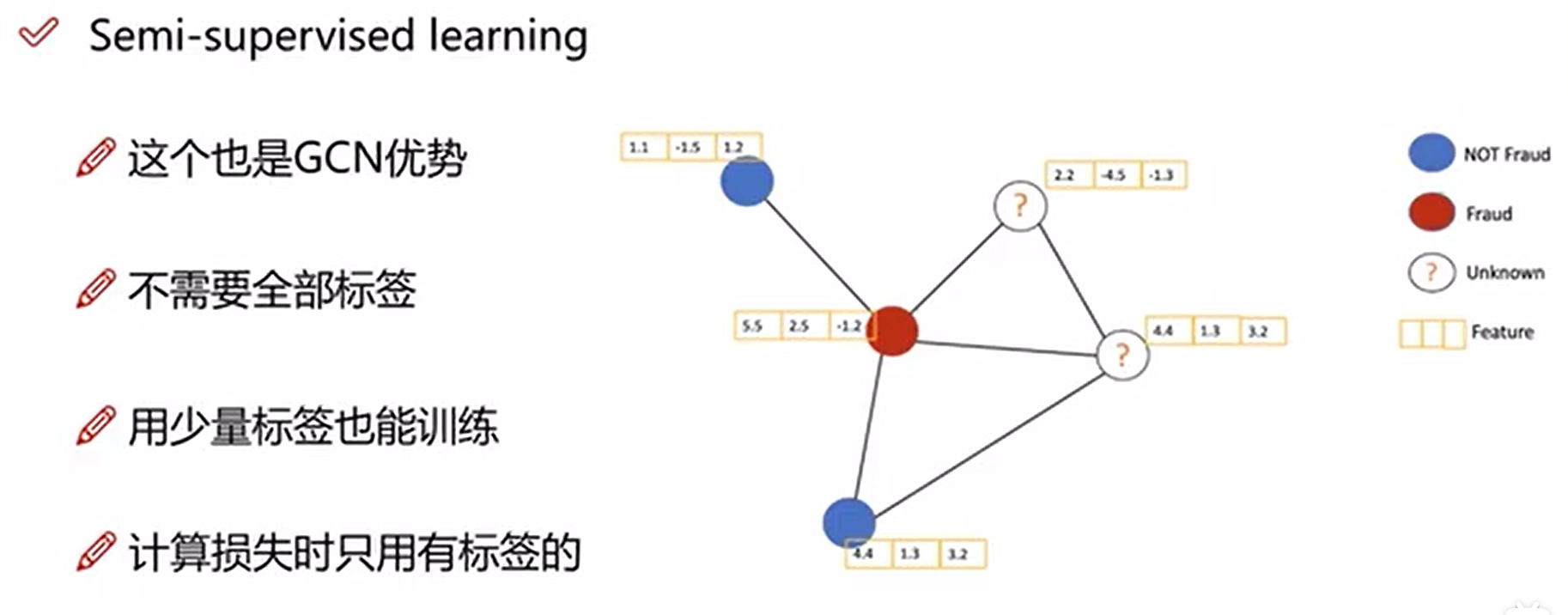
半监督学习
GCN属于半监督学习(不需要每个节点都有标签都可以进行训练)
计算Loss时,只需要考虑有标签的节点即可。
为了减少有标签节点的Loss,其周围的点也会做相应的调整,这也是图结构的特点,因此GNN和GCN中,不需要所有节点都有标签也可以进行训练(当然至少需要一个节点有标签)
GCN的计算
图中基本组成
特征计算方法
邻接矩阵的变换
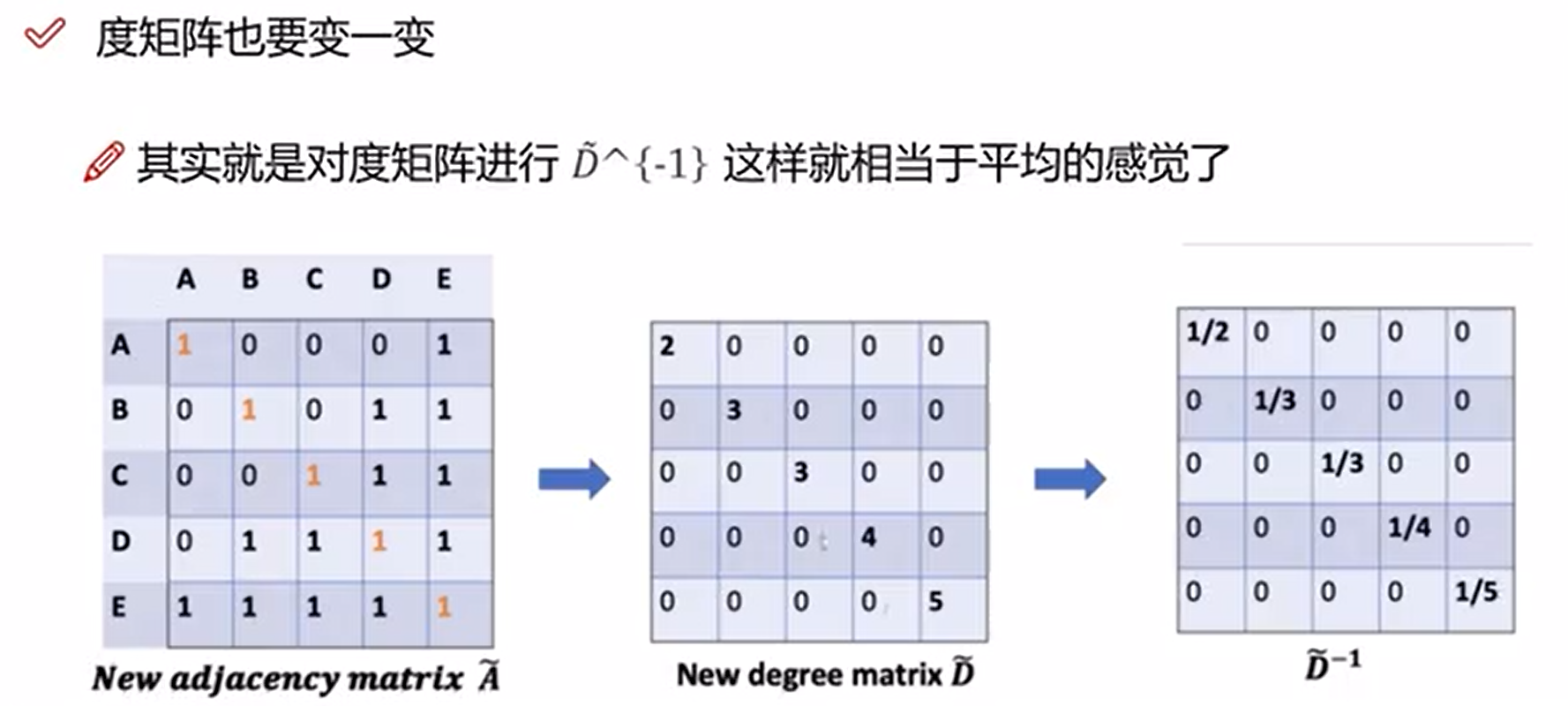
但是现在存在一个问题:一个节点的度越大,其做矩阵乘法后的值就越大(累加次数变多了),这种情况是不好的(相当于一个人认识的人越多,其的特征值就越大,这样不好)
为了解决这个问题,我们需要对度矩阵求倒数,相当于平均的感觉,对度数大的节点加以限制
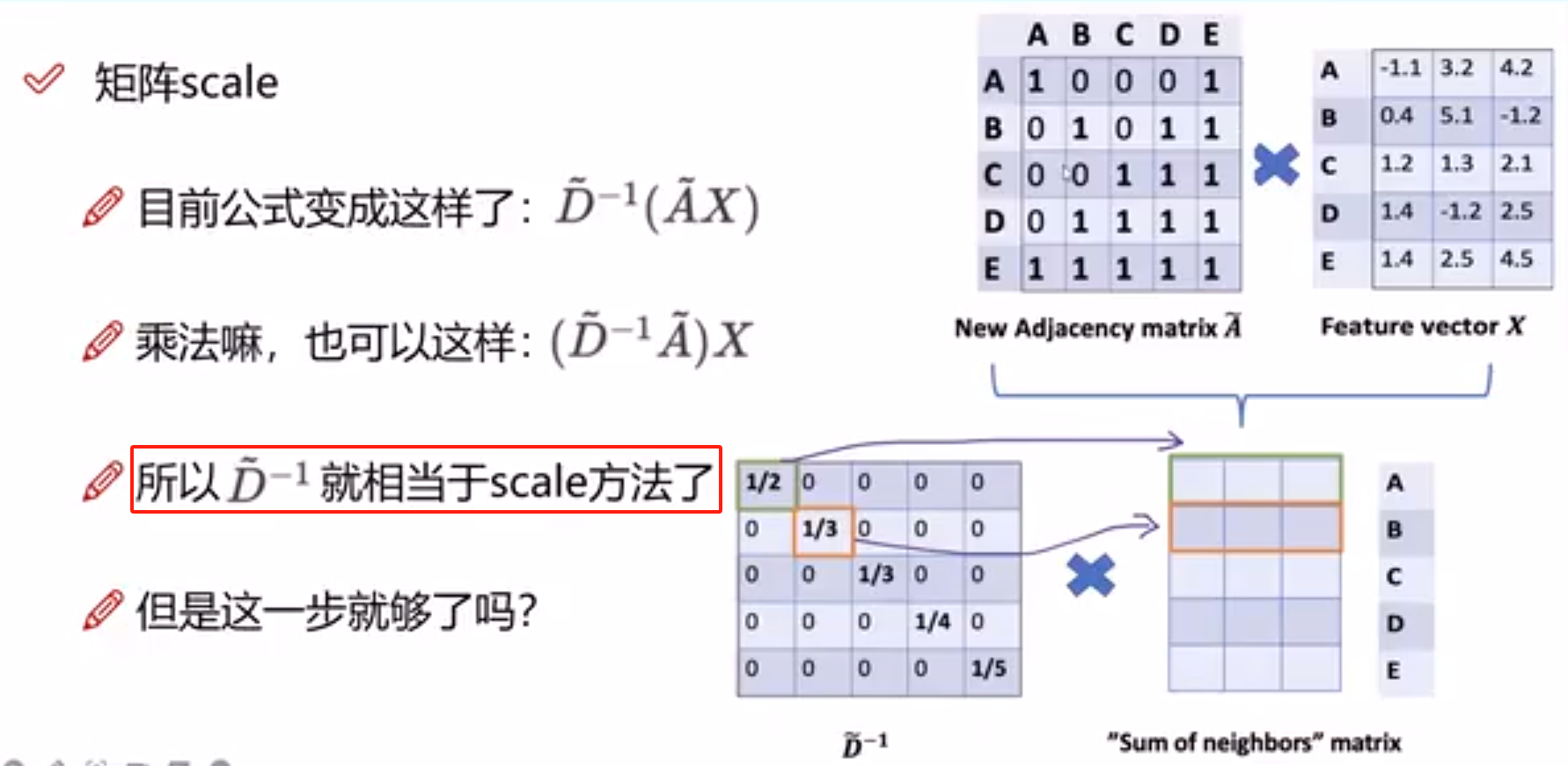
上面的左乘相当于对行做了归一化操作,那么列也需要做归一化操作
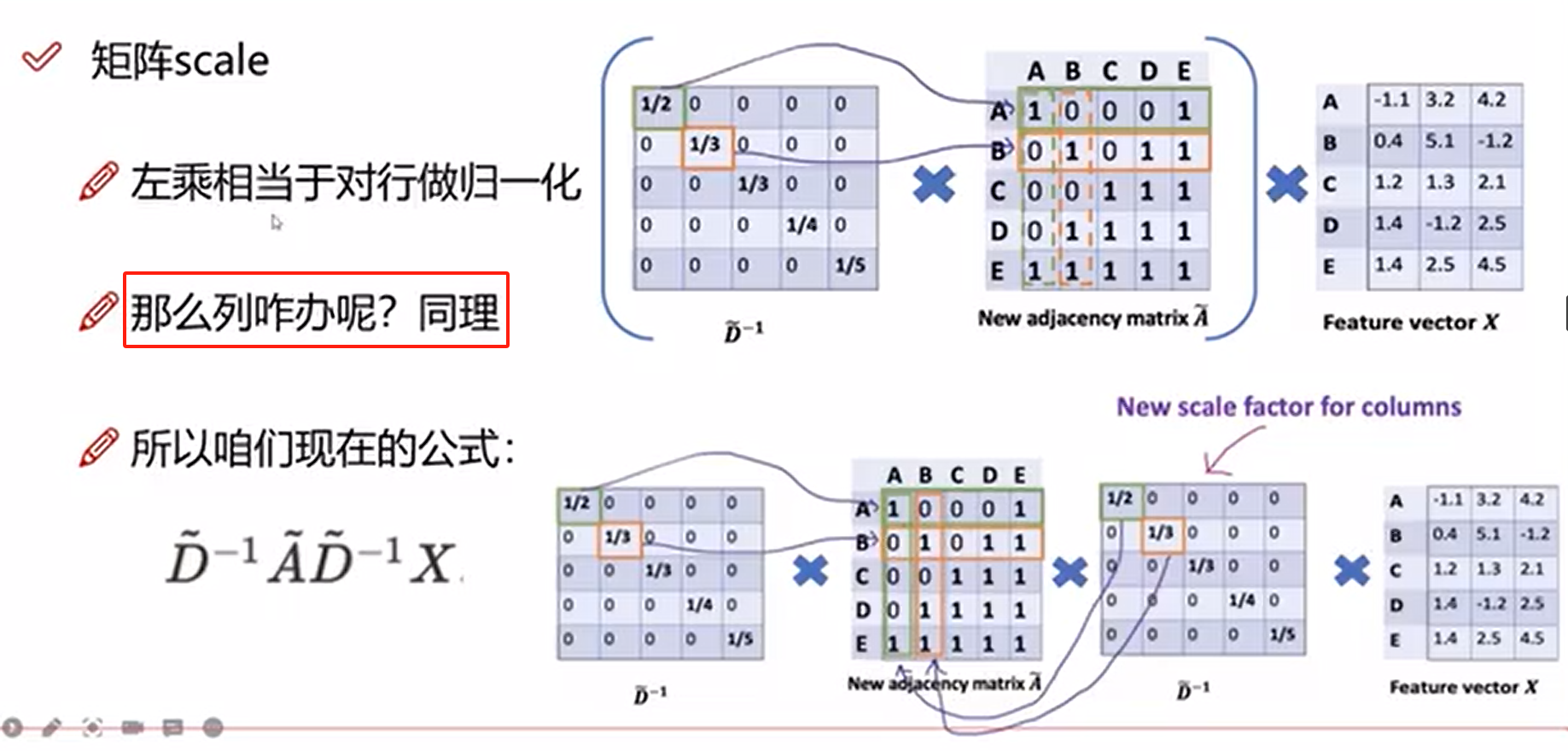
但是又有问题了,行和列都做了归一化,那不是会存在2次归一化的情况吗(行列重叠处)
所以我们需要在度矩阵倒数那加一个0.5次方来抵消这个2次归一化的影响
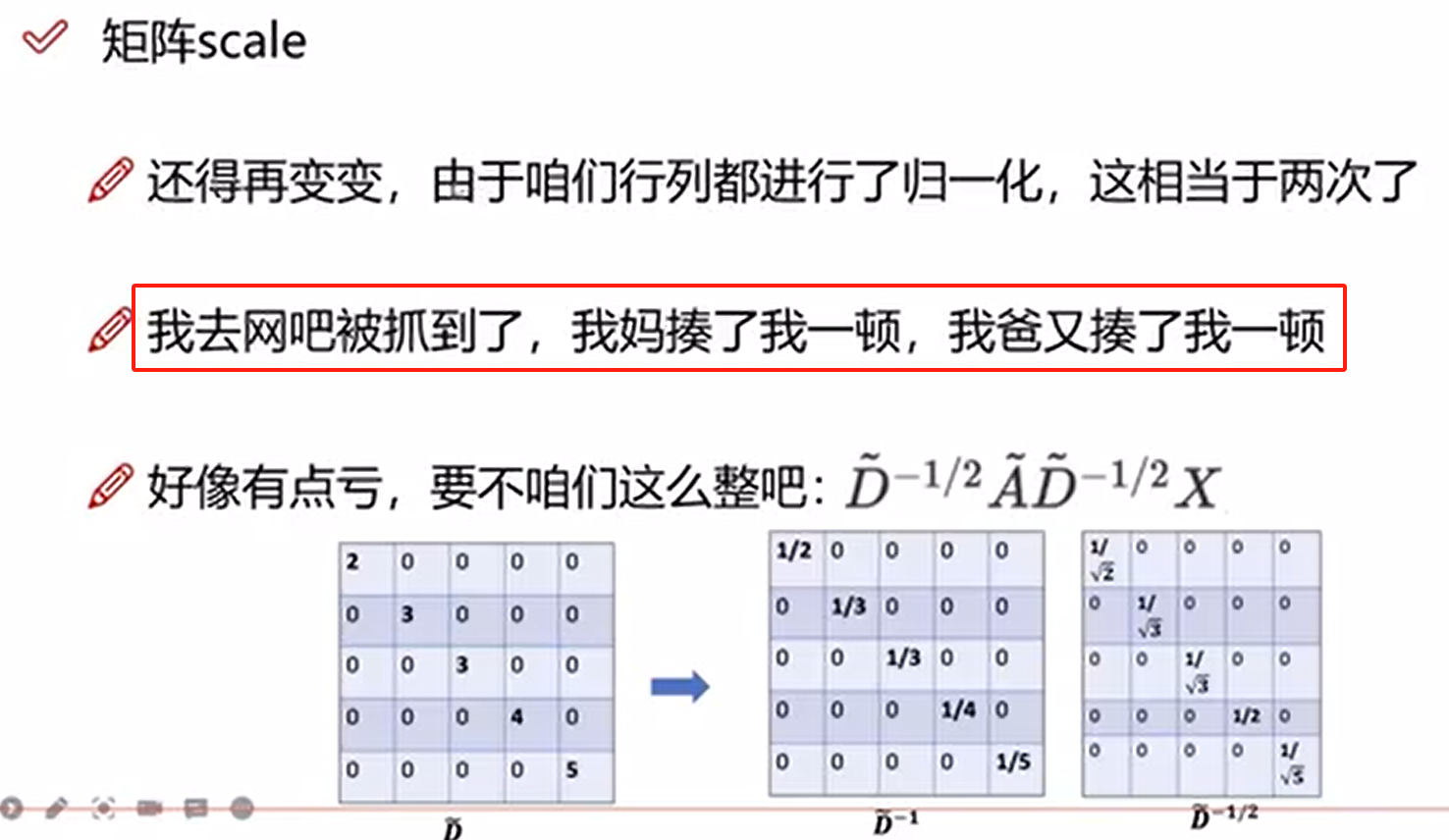
GCN层数
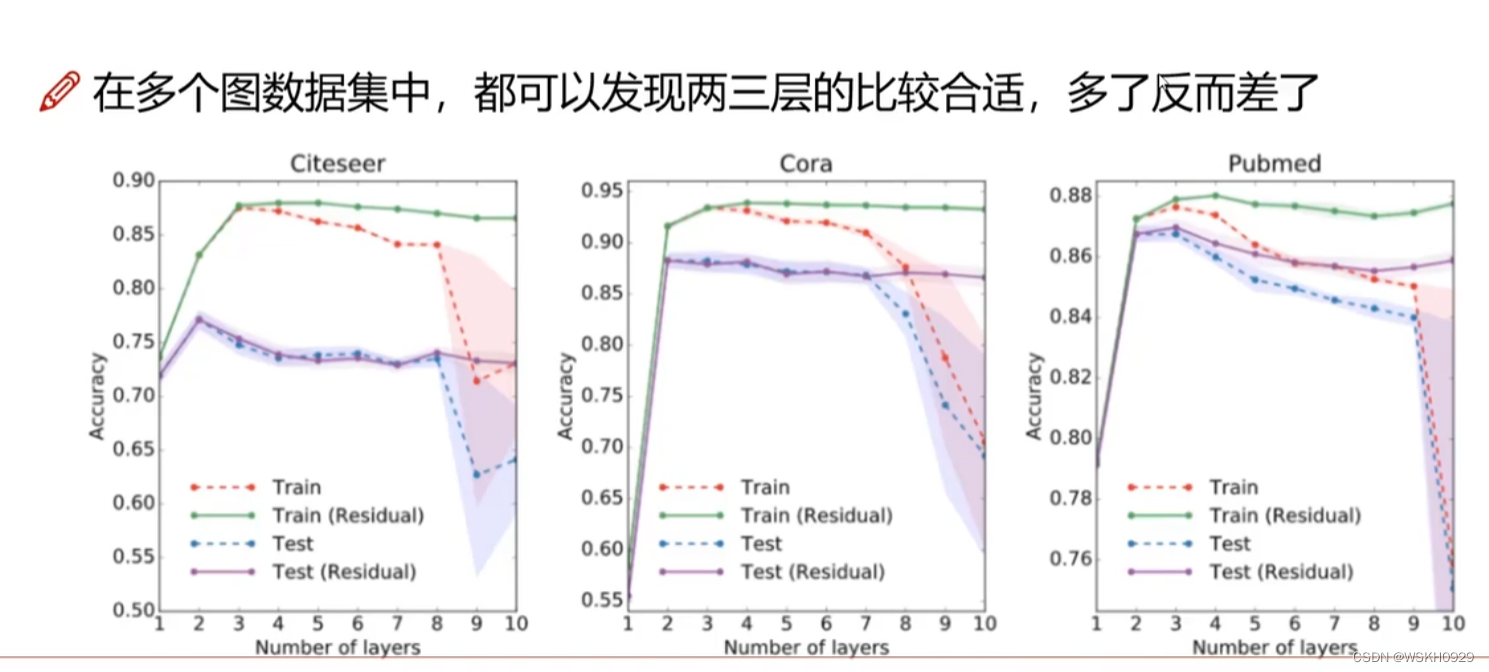
图卷积也可以做多层,但是一般不做太深层,一般只做2-3层(类似于一种说法,你只需要认识6个人就可以认识全世界)
实验表明:GCN中,深层的网络结构往往不会带来更好的效果。
直观解释:我表哥认识的朋友的朋友的朋友的朋友认识市长,不代表我和市长关系就很好。
层数越多,特征表达就越发散,一般2-5层即可
参考资料
A Gentle Introduction to Graph Neural Networks
零基础多图详解图神经网络(GNN/GCN)【论文精读】
不愧是公认最好的【图神经网络GNN/GCN教程】,从基础到进阶再到实战,一个合集全部到位!
图神经网络7日打卡营
图神经网络简介,什么是图神经网络,GNN
【图神经网络实战】深入浅出地学习图神经网络GNN(上)