【深蓝学院】手写VIO第6章--视觉前端--笔记

第5章相关内容，还是CSDN的传统Markdown编辑器好用。
视觉前段在14讲课程中已经讲过，这里再简单复习一下。

1. 前端工作的定性比较，分析

这一节讲了很多关于前端的方法框架的对比讨论，后面看完了相关的论文之后强烈建议再回来听一听本章的第一节课。
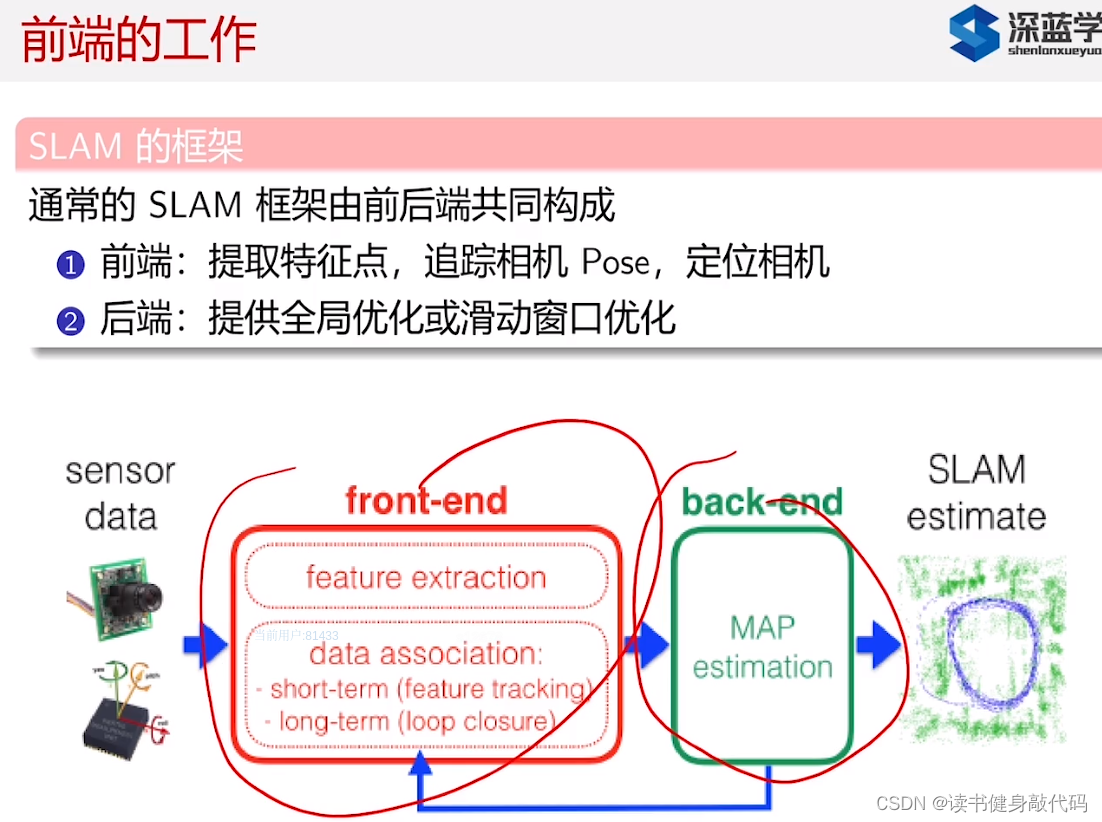
在这里插入图片描述
前端和后端不太一样，前端没办法放在同一个框架中把不同方法进行对比(如光流法和特征匹配法)，因为可能不同方法在其特定的工况下都能正常工作。

前端实现上的现实问题
在这里插入图片描述
实际上那个，前端在SLAM最终精度上的影响比后端更大，体现出来的更直观，比如某一段没有跟踪上之类的，可能就会影响整体的精度。

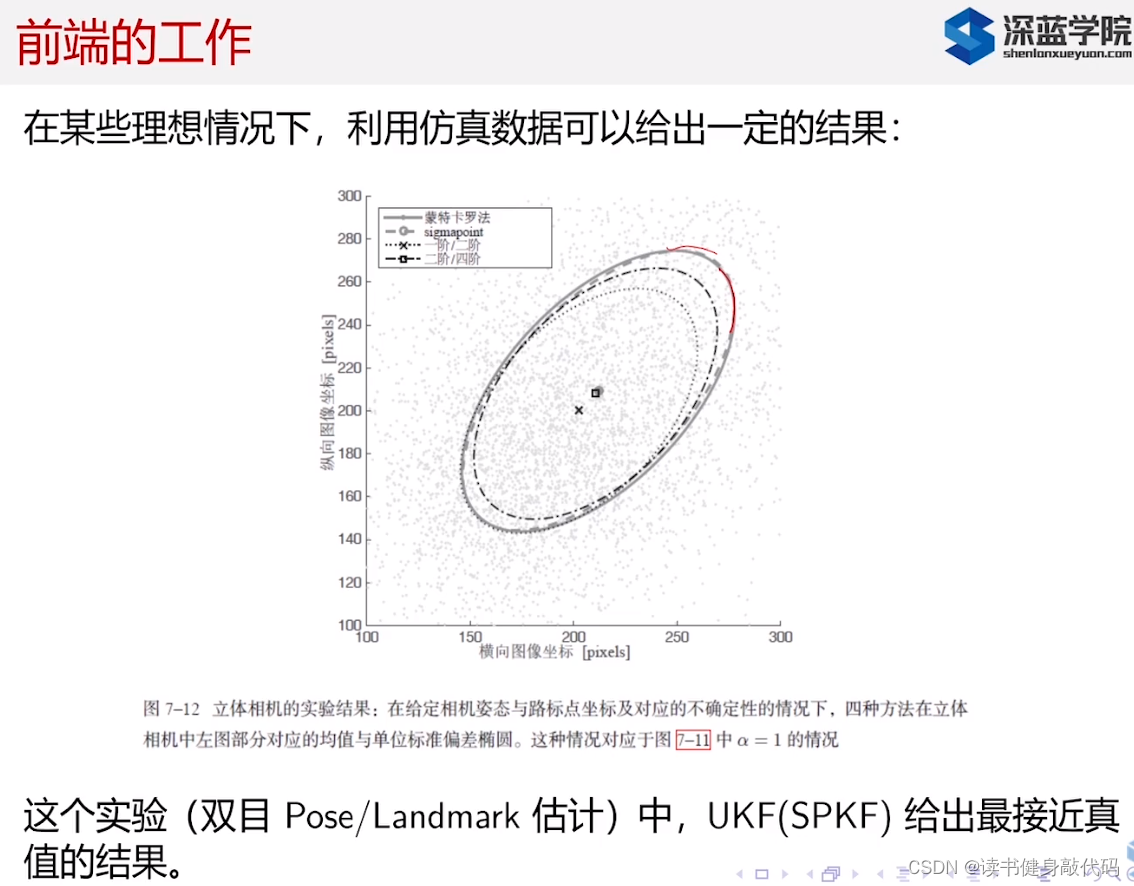
在这里插入图片描述
比如一次仿真中，假设数据和噪声都服从Gaussian distribution，用UKF得到了较好的实验结果，但是在实际情况中可能并不都符合Gaussian distribution，所以这个结论不一定是能够很好地泛化的，overfitting了。

比如有local mapping，sliding window，理论上来说全局的marg会更好，到那时实际中全局的marg计算力量过大，不太易实现，具体看后端能够有多大的算了和空间来做，如果没有的话可能就用个EKF就行了。
不同数据集间精度的对比没有什么意义，Kitti场景简单，动的物体比较少，EUROC可能已经做到头了；TUM-Mono难一点，场景较多，有过门，过墙之类的。
在这里插入图片描述
前端因为方法不同（比如特征点法第一步提特征点，直接法第一步求梯度，这些方法都不同，很难在方法内（范式内，先这样理解）进行对比，只能在整个系统之间（范式间）进行对比）。

直接法基于灰度不变假设，相对于PnP来说多了乘了个像素梯度，即若该店的梯度为0，则对T的估计无用，故倾向于选择有梯度的点，且梯度越大贡献越大。

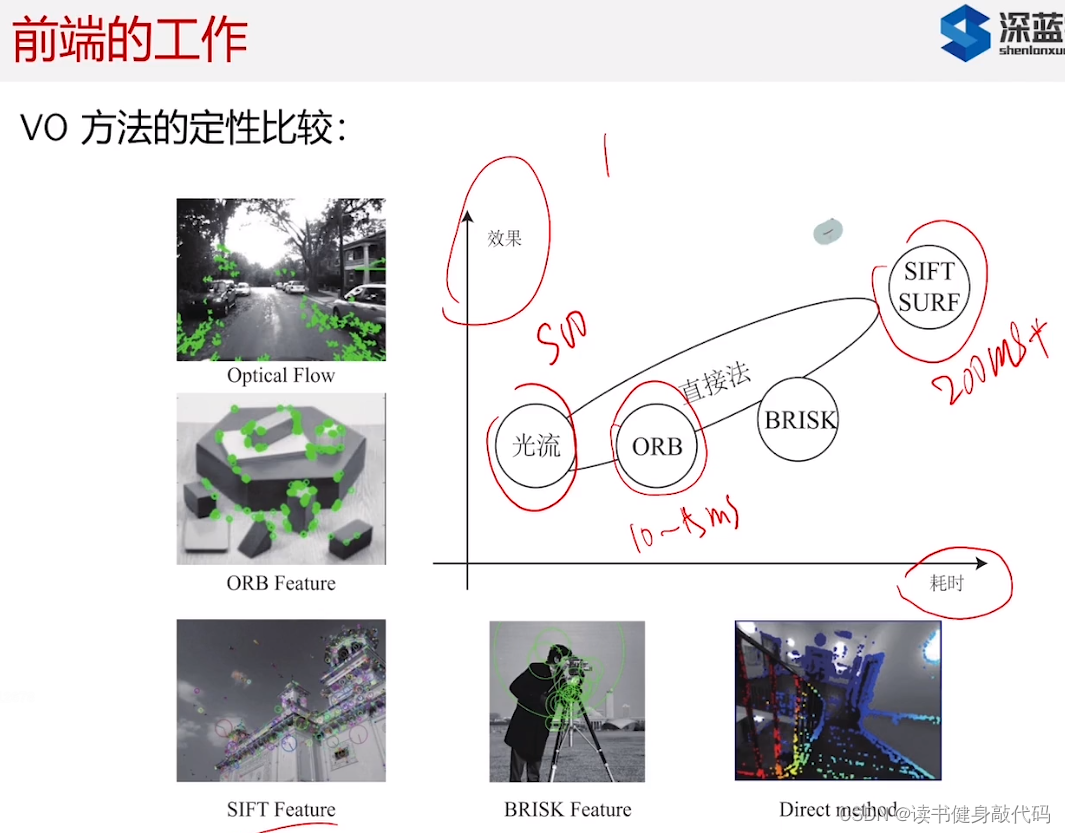
在这里插入图片描述

很多地方直接法都比特征点法好，因为可能没办法提取到足够多特征点且容易feature lost。（高翔的主观感受，具体还是需要自己去跑一跑）

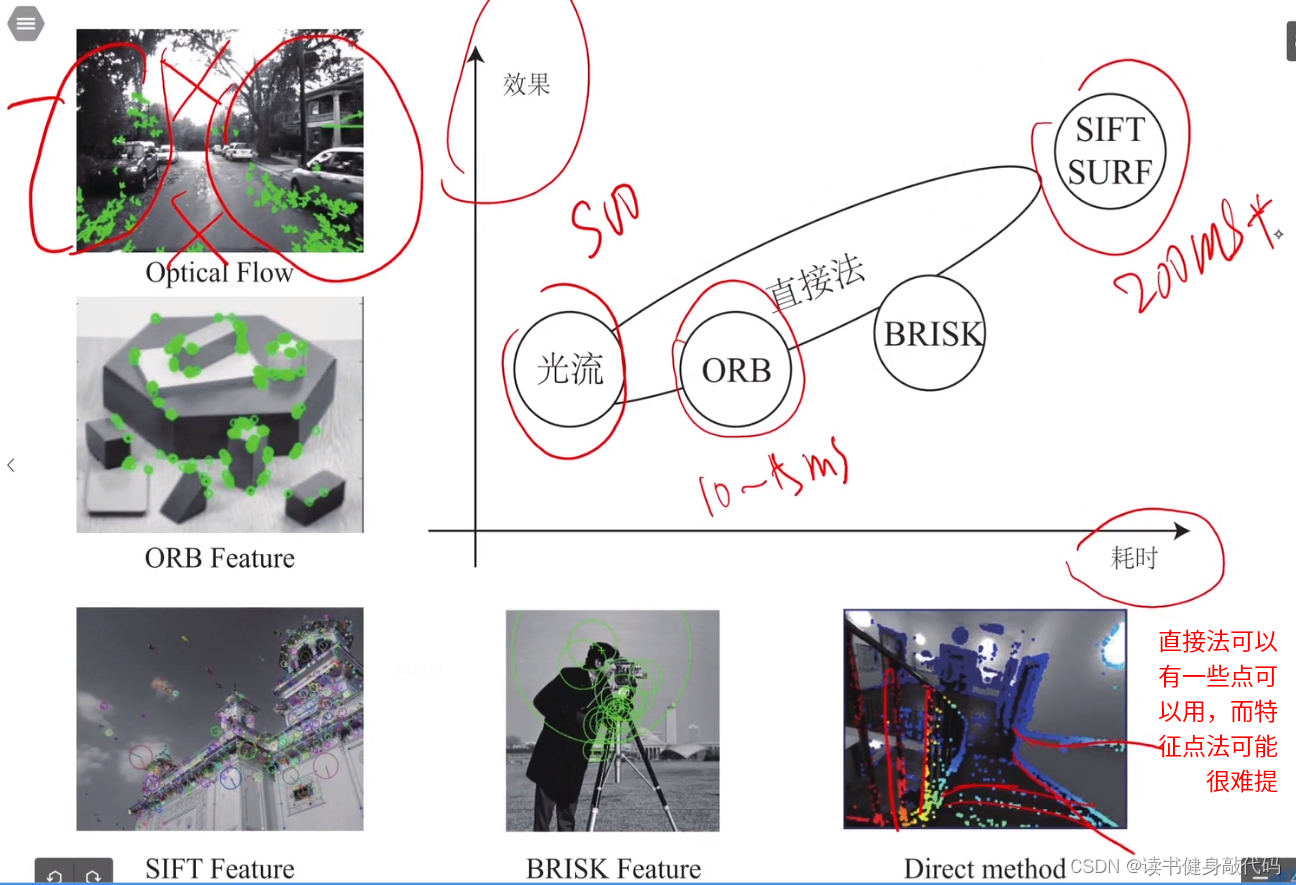
在这里插入图片描述

光流法：PTAM，Tango，现在比较成熟，但缺点也明显；
FAST+光流，GFTT+光流：很实用，很快；
特征匹配：SIFT，FURF匹配的最好，但是计算量大；
特征匹配和光流都依赖角点，提不出来的场景无法使用。

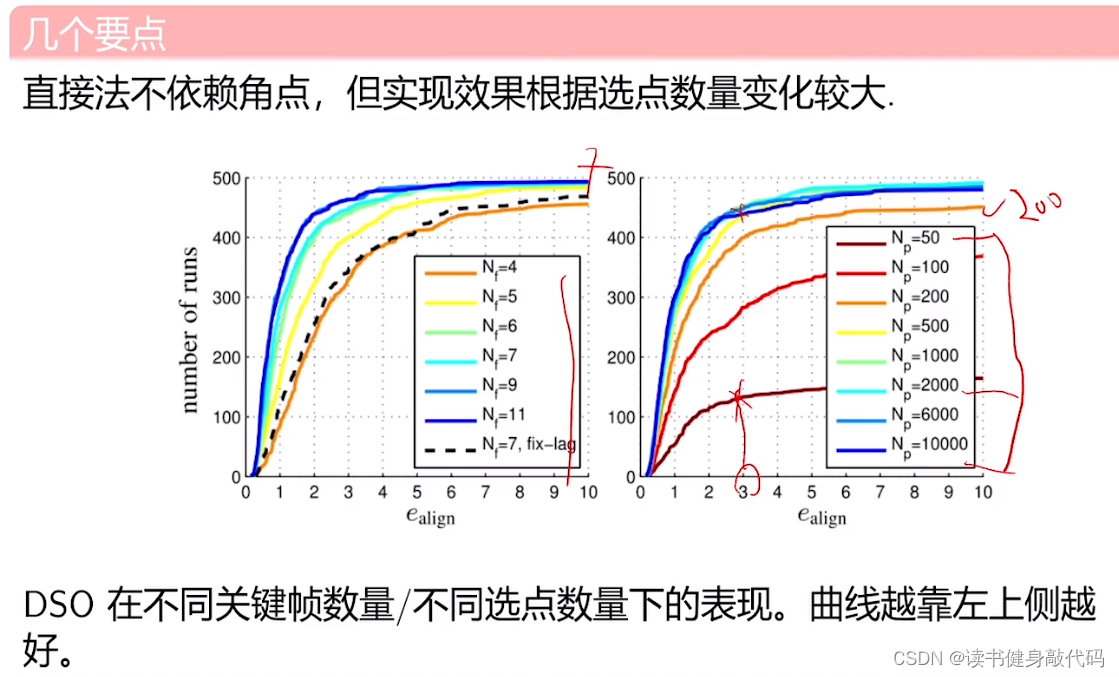在这里插入图片描述 DSO达到某个误差（如小于3）所需的迭代次数，发现跟使用额KF数量和选点数量有关。

2. 前端介绍（以光流来展开）

上手可以用FAST+光流来做一个看看效果。
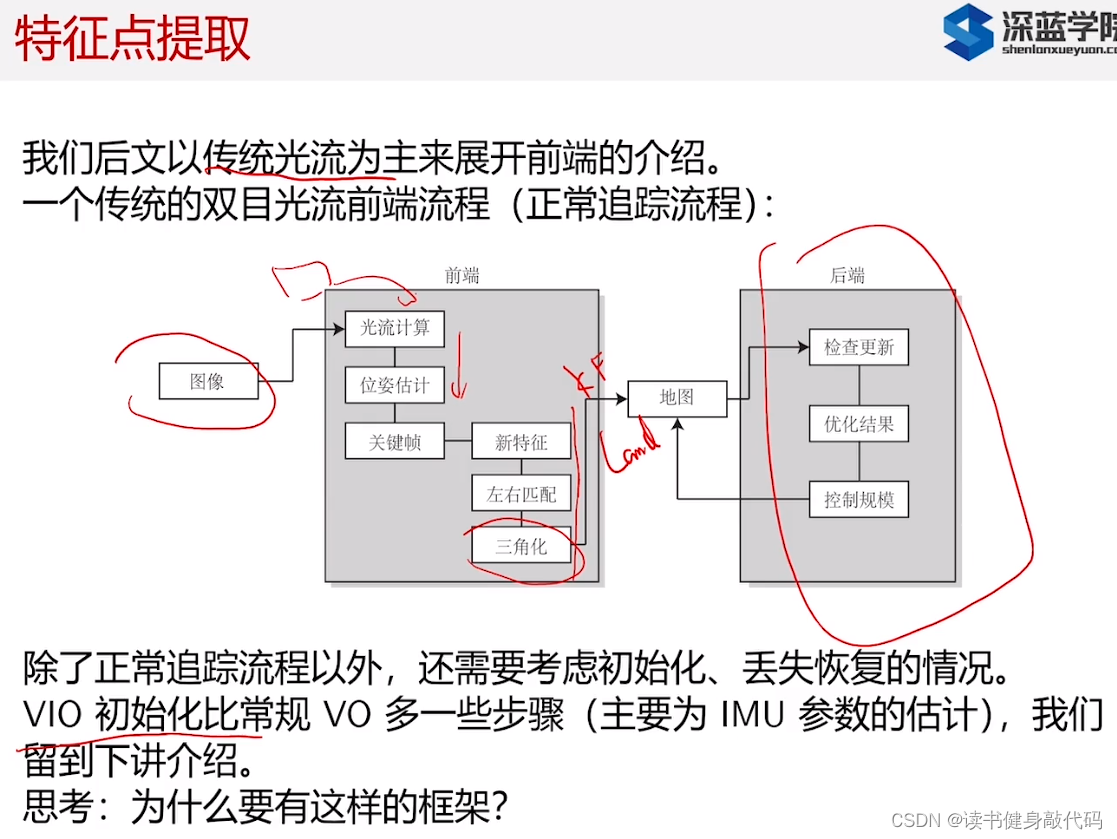
在这里插入图片描述
VIO的初始化需要讨论一下，下一节讨论。
有一个问题：对于前端，如何保证整体框架是最优的？即第一步计算光流，第二部估计pose…每一步的操作可以保证是最优的，但是没办法保证整体这个前端框架是最优的，大多数是工程上的经验，只要这样做就能得出还不错的结果。你也可以直接搞一个神经网络，输入imgs输出一堆poses和landmarks，

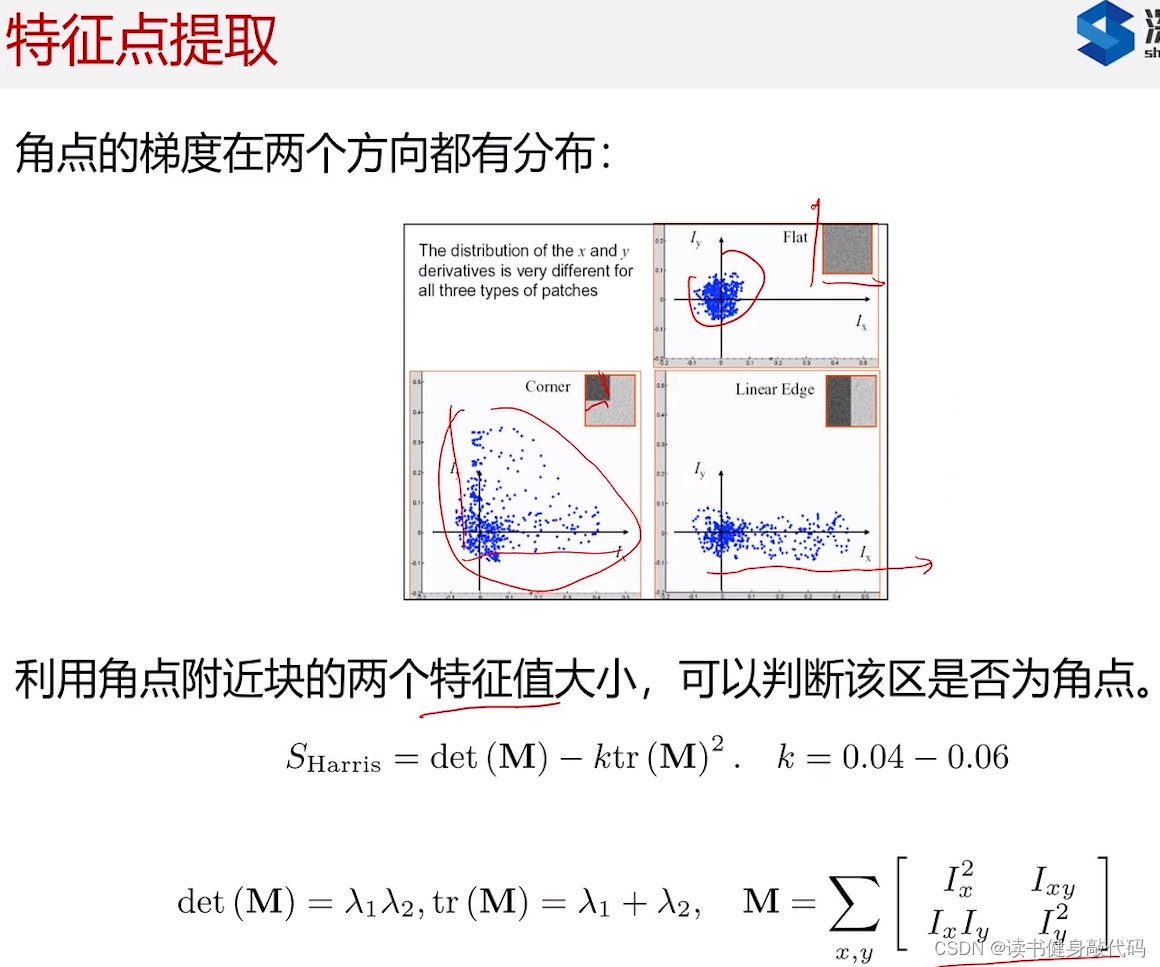
在这里插入图片描述
特征提取方法在CV普及开来之前就已经研究出来了，如角点主要看两个方向的梯度分布，对矩阵进行特征值分解（奇异值分解，平方之后就是特征值？特征值体现的是在两个方向上的分布情况）：

如果两方向梯度都接近于0，倾向于是平坦区域(flat)。
如果两个方向都比较大，倾向于角点(Corner)。
如果是一方向较大，另一方向较小，倾向于边(Edge)。

具体实现：Harris提出了一个判断方法，计算 $S_{Harris}$ 指标，

如果两个都小，则 $S_{Harris}$ 接近0，
如果都很大，则整体很大，
如果一大一小，则结果不大不小，
设置阈值来判断是否为Corner

在这里插入图片描述
在Harris基础上改进了评分方式，可以指定选点的个数，根据选点个数来确定比较的阈值。

在这里插入图片描述
warp光流：对于光流的改进。由于视角可能会发生变化，特征块也会变化，所以要对特征块进行变换使得变换之后的特征块更像待追踪的块（常取仿射变换），在优化过程中，变换的参数还可以调整，以在线估计最优的变换参数。
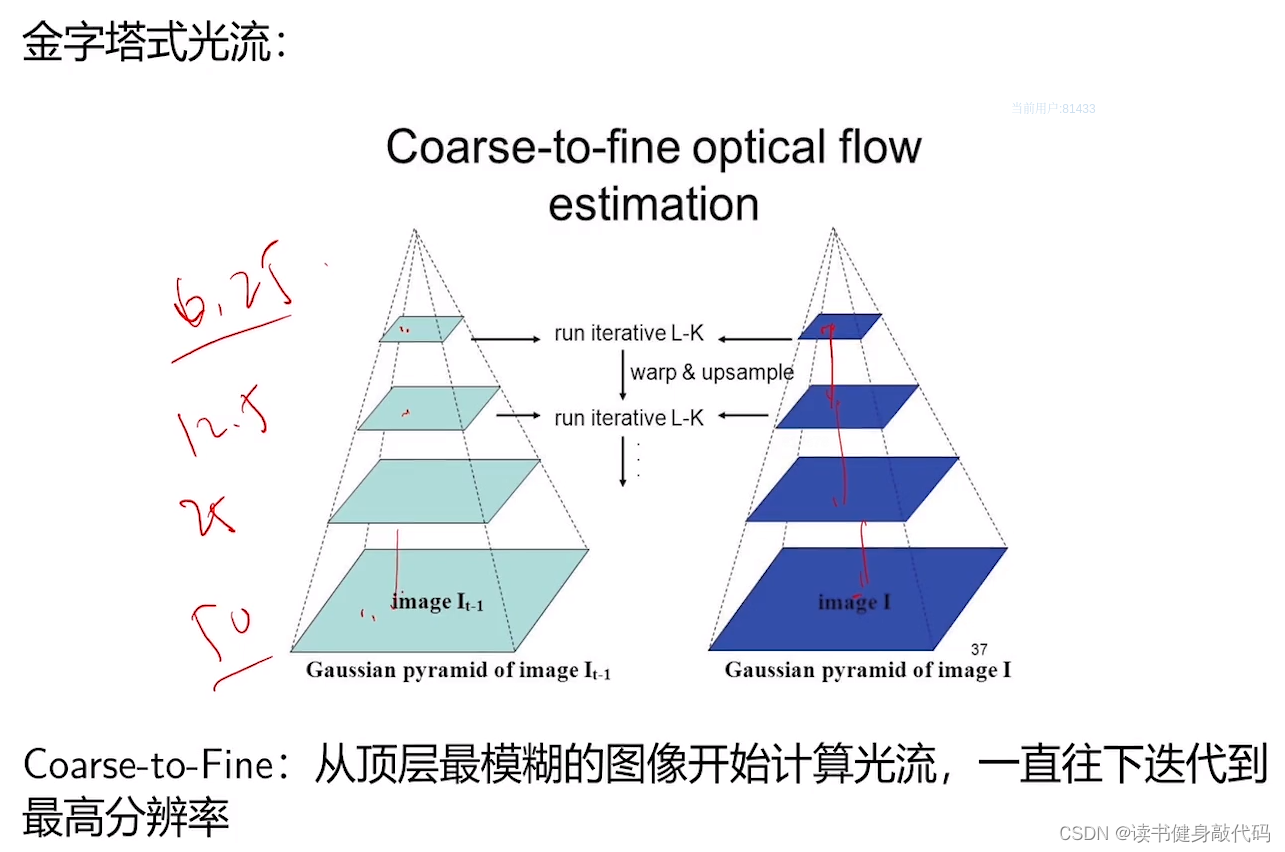
在这里插入图片描述
还可以给Warp光流加上金字塔，对高速运动的场景效果更好

在这里插入图片描述

不能远距离track，一个具体例子：如果相机不动，有人从面前走过，期间过了100帧图像，那么可能第1帧和第100帧就无法track上了。
工程上的解决方法例如track with map，上面的方法是track weith last( $I_k$ 和 $I_{k-1}track$ )或者是recent，当做完之后再跟地图去比，把地图中的一些点往投到 $I_k$ 中投，发现能够投过来，然后再把 $I_k$ 和 $I_1$ 进行对比，看改点能否被track。
远近这种场景比较常见，比如远处是空白，但是近处发现有纹理。
角点对效果好，边效果不好
稀疏光流约束差，可能存在outlier，如稠密光流约束附近的点的亮度差不多，但稀疏没有。

3. 关键帧与三角化

3.1. 关键帧

在这里插入图片描述

关键帧是为了减小问题规模，使得后端能够计算得过来
处理相机停止的情况，避免后端退化：如果不挑选KF，camera 不动会导致逆深度计算错误，逆深度变成不可观的，有多个解。
关键帧选择：
不能太近：太近可能退化，或者三角化算不出深度
不能太远：太远可能共视点过少，丢掉中间的motion

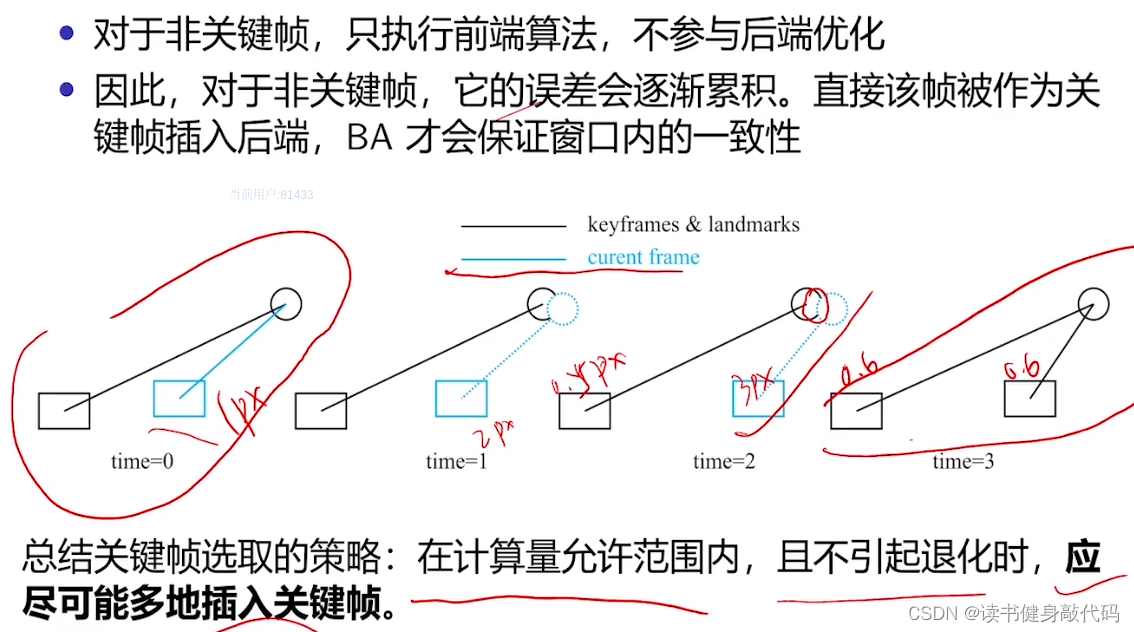
在这里插入图片描述
非KF只算前端，不进后端。
插入KF的一个策略：在后端算力的允许的情况下，尽可能多地插入KF，因为KF对后端是友好的（光束法平差，误差均摊，整体误差变小）

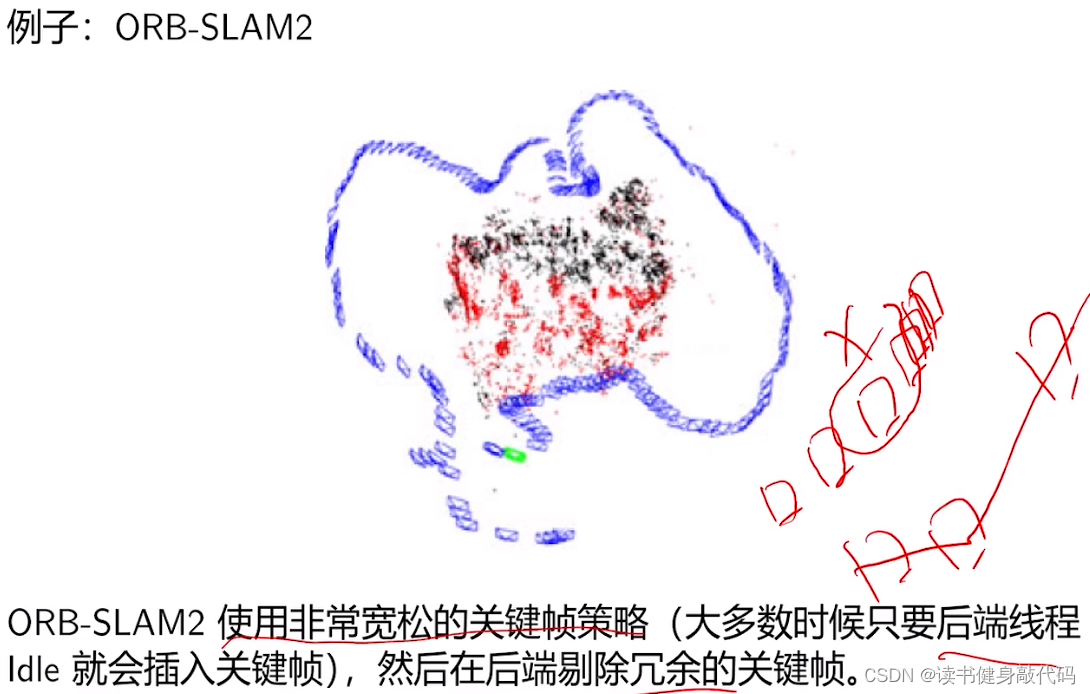
在这里插入图片描述
ORB_SLAM2后端有个local mapping，只要该线程idle时就插KF，然后对于冗余的再删掉。

DSO使用了sliding window，窗口内保持5~7个KF，并保持一定的展开，老的几帧，中等的几帧，最新的几帧，有以下策略

对于老的关键帧，将其中的landmark投到新的里面去，如果新的里面没有观测到这些landmark，则marg掉老的KF。
每个KF都有最小寿命，防止刚进来就被marg。

3.2. 三角化

在这里插入图片描述
三角化的条件和时间，有的方法只在KF上提Feature，有的每帧都提。前者计算量很小，但是可能导致三角化时点不够，效果不好；后者计算量大但是效果好。

在这里插入图片描述
取(10)第3行，带入(10)，取钱两行可得(12)，这里说一下矩阵的维度，
$P_k$ ：3*4，每行系数都是1*4，即 $P_{k,1}^T,P_{k,2}^T,P_{k,3}^T$ 都是4*1
$y$ ：4*1
(13)中D矩阵每行都是4*1，由于每次观测会有u,v两个方程，所以一次观测就是 $(2 * 1) * 4$ 行的D，n此就是 $2 n * 4$ 行。
在这里插入图片描述

求解
在这里插入图片描述

在这里插入图片描述

作业待解：为什么取 $y=u_4$
由于系数矩阵容易满秩，故寻求最小二乘的数值解，对 $D^TD$ 进行奇异值分解(SVD)，分解出的奇异值一般是从大到小排列， $D^TD$ 是 $4 * 4$ 的，4个奇异值，判断该解是否有效（判断三角化是否成立），看 $\sigma_4<<\sigma_3$ (经验上取1e-2~1e-4算远小于，也可以卡得更严一点更小一点)是否成立， $\sigma_1\sigma_2 \sigma_3$ 组成了一个三维的空间， $\sigma_4$ 是零空间
D的数值可能不稳定，数值过大的话会导致较小值的影响体现不出来，需要对D进行rescale，取值方法取为一个对角阵，取D最大元素之逆。
还需要检测深度是否满足正确条件。