文章目录
- 一:基本介绍
- 1.1 概念
- 1.2 算法思想
- 1.3 思路分析图
- 1.4 思路分析
- 1.5 总结
- 1.5.1 选择排序一共有数组大小-1轮排序
- 1.5.2 每一轮排序,又是一个循环,循环的规则如下(在代码中实现):
- 二:代码实现
- 2.1 源码
- 2.2 执行结果
- 2.3 测试八万条数据
- 三:算法性能分析
- 3.1 时间复杂度
- 3.2 空间复杂度
- 3.3 稳定性
一:基本介绍
1.1 概念
选择排序(select sorting)属于内部排序法,是从待排序的数据中,按指定的规则选出某一元素,再按照规定交换位置后达到排序的目的。
1.2 算法思想
第一次从arr[0] ~ arr[n-1]中选取最小值,与arr[0]交换,第二次从arr[1] ~arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2] ~ arr[n-1]中选取最小值,与arr[2]交换,…,第i次从arr[i-1] ~arr[n-1]中选取最小值,与arr[i-1]交换,…, 第n-1次从arr[n-2] ~arr[n-1]中选取最小值,与arr[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
每一次从待排序的数据元素中选出最小(或最大)的一个元素,将元素存放在序列的起始位置(即与待排序列的第一个元素的位置进行交换)。然后再从剩余的未排序元素中寻找最小(或最大)的元素,然后存放在已排序序列的末尾。以此类推,直到将待排序的元素全部排完。
1.3 思路分析图

1.4 思路分析
原始数组:[86, 21, 156, 6]
第一次排序: 从4个元素里面找到最小的,与第1个元素进行交换,将最小元素存放在起始位置
排序后为:6,21 , 156, 86
第二趟排序: 从剩下的3个元素里面找到最小的,与待排序列的第1个元素进行交换,将最小元素存放在已经排好序的序列尾部。
排序后为:6,21 , 156, 86
第三趟排序: 从剩下的2个元素里面找最小的,与待排序列的第1个元素进行交换
排序后为:6,21 , 86,156
1.5 总结
1.5.1 选择排序一共有数组大小-1轮排序
1.5.2 每一轮排序,又是一个循环,循环的规则如下(在代码中实现):
- 先假定当前这个数是最小数
- 和后面的每个数进行比较,如果发现有比它更小的数,就重新确定最小数,并得到下标
- 当遍历完数组之后,就会得到本轮最小数及其下标
- 进行交换
二:代码实现
2.1 源码
import java.util.Arrays;/*** 选择排序*/
public class SelectSort {public static void main(String[] args) {int[] array = new int[8];for (int i = 0; i < array.length; i++) {//Math.random() * 80000生成0到100的随机数array[i] = (int) (Math.random() * 100);}System.out.println("排序前:" + Arrays.toString(array));selectSort(array);System.out.println("排序后:" + Arrays.toString(array));}/*** 选择排序** @param array 需要排序的数组*/public static void selectSort(int[] array) {//使用逐步推倒的方式来讲解选择排序//第一轮//原始的数组:101,34,119,1//第一轮排序:1,34,101,119//算法先简单-->后复杂。可以将复杂算法简单化for (int i = 0; i < array.length - 1; i++) {//第一轮//假定最小处的索引就是0int minIndex = i;//最小处的数值则为int min = array[minIndex];for (int j = i + 1; j < array.length; j++) {if (min > array[j]) {//如果此条件成立,说明假定的最小值就不成立//此时我们需要重置最小值minIndex = j;min = array[minIndex];}}//交换之前需要进行判断if (minIndex != i) {//for循环结束后则最小值就已经找到了,此时我们需要将下标为0处的数重新替换为最小值//将原本最小值的位置替换为array[0]array[minIndex] = array[i];//将最小值放在array[0],即交换array[i] = min;}System.out.println("第" + i + "轮过后排序为:" + Arrays.toString(array));}}
}
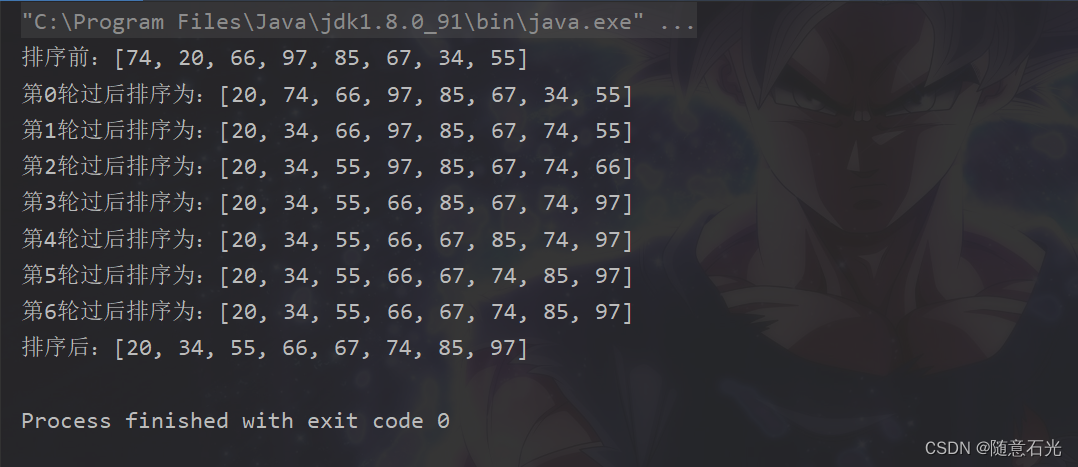
2.2 执行结果
2.3 测试八万条数据
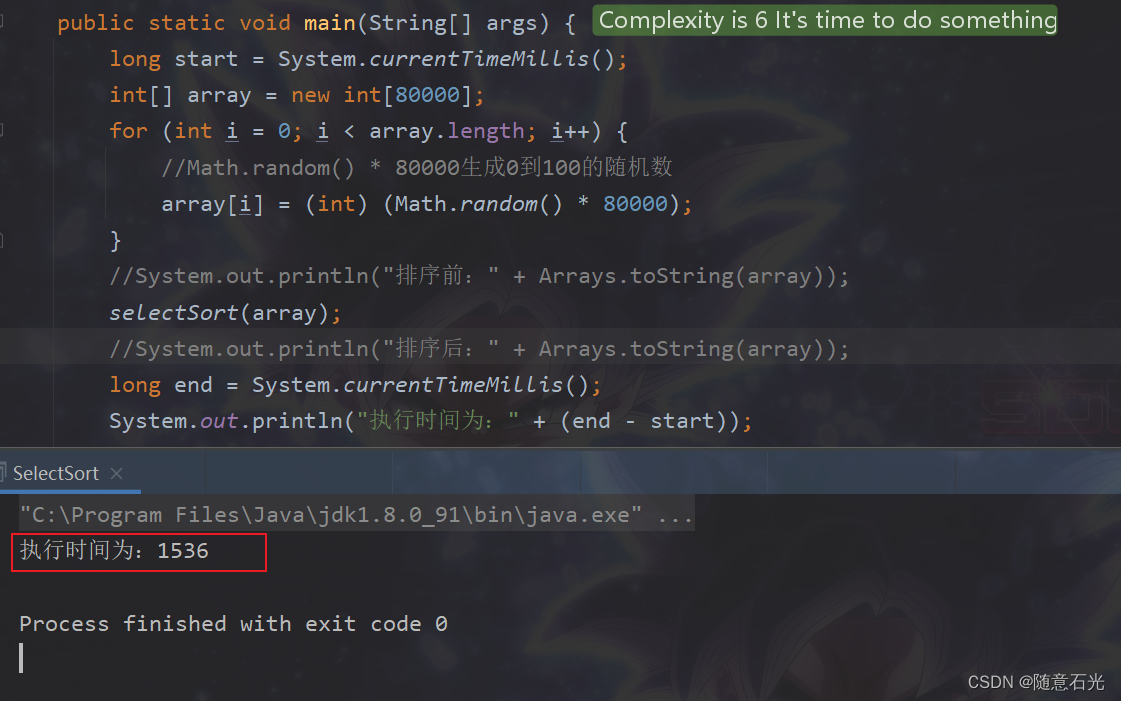
八万个数据的排序时间是1536毫秒,很明显是比冒泡排序短很多的!
三:算法性能分析
3.1 时间复杂度
最优时间复杂度、最坏时间复杂度、平均时间复杂度都是O(n^2),因为无论你是否完全有序,还是完全逆序,都需要找出后边的最小值进行替换。
相比较冒泡排序,每次比较后,只更新最小值的下标,每轮循环值最多只做一次值交换。时间上得到了很大的提升。但是也是使用了双层循环,时间复杂度和冒泡排序的一样。
3.2 空间复杂度
空间复杂度为O(1)
3.3 稳定性
选择排序是不稳定的排序算法。
举个例子:
例如数组:[ 5 , 8 , 5 , 2 ]
使用选择排序算法第一次找到的最小元素是2,与第一个位置的元素5进行交换,那此时第一个5和中间的5顺序就发生了变化,因此不稳定。