文章目录
- 双周赛114
- [2869. 收集元素的最少操作次数](https://leetcode.cn/problems/minimum-operations-to-collect-elements/)
- 模拟
- [2870. 使数组为空的最少操作次数](https://leetcode.cn/problems/minimum-number-of-operations-to-make-array-empty/)
- 哈希 + 枚举
- [2871. 将数组分割成最多数目的子数组](https://leetcode.cn/problems/split-array-into-maximum-number-of-subarrays/)
- AND 位运算性质
- [2872. 可以被 K 整除连通块的最大数目](https://leetcode.cn/problems/maximum-number-of-k-divisible-components/)
- DFS
双周赛114
2869. 收集元素的最少操作次数
简单
给你一个正整数数组 nums 和一个整数 k 。
一次操作中,你可以将数组的最后一个元素删除,将该元素添加到一个集合中。
请你返回收集元素 1, 2, ..., k 需要的 最少操作次数 。
示例 1:
输入:nums = [3,1,5,4,2], k = 2
输出:4
解释:4 次操作后,集合中的元素依次添加了 2 ,4 ,5 和 1 。此时集合中包含元素 1 和 2 ,所以答案为 4 。
示例 2:
输入:nums = [3,1,5,4,2], k = 5
输出:5
解释:5 次操作后,集合中的元素依次添加了 2 ,4 ,5 ,1 和 3 。此时集合中包含元素 1 到 5 ,所以答案为 5 。
示例 3:
输入:nums = [3,2,5,3,1], k = 3
输出:4
解释:4 次操作后,集合中的元素依次添加了 1 ,3 ,5 和 2 。此时集合中包含元素 1 到 3 ,所以答案为 4 。
提示:
1 <= nums.length <= 501 <= nums[i] <= nums.length1 <= k <= nums.length- 输入保证你可以收集到元素
1, 2, ..., k。
模拟
class Solution {public int minOperations(List<Integer> nums, int k) {Set<Integer> set = new HashSet<>();for(int i = nums.size()-1; i >= 0; i--){if(nums.get(i) <= k){set.add(nums.get(i));if(set.size() == k) return nums.size() - i;}}return nums.size();}
}
2870. 使数组为空的最少操作次数
中等
给你一个下标从 0 开始的正整数数组 nums 。
你可以对数组执行以下两种操作 任意次 :
- 从数组中选择 两个 值 相等 的元素,并将它们从数组中 删除 。
- 从数组中选择 三个 值 相等 的元素,并将它们从数组中 删除 。
请你返回使数组为空的 最少 操作次数,如果无法达成,请返回 -1 。
示例 1:
输入:nums = [2,3,3,2,2,4,2,3,4]
输出:4
解释:我们可以执行以下操作使数组为空:
- 对下标为 0 和 3 的元素执行第一种操作,得到 nums = [3,3,2,4,2,3,4] 。
- 对下标为 2 和 4 的元素执行第一种操作,得到 nums = [3,3,4,3,4] 。
- 对下标为 0 ,1 和 3 的元素执行第二种操作,得到 nums = [4,4] 。
- 对下标为 0 和 1 的元素执行第一种操作,得到 nums = [] 。
至少需要 4 步操作使数组为空。
示例 2:
输入:nums = [2,1,2,2,3,3]
输出:-1
解释:无法使数组为空。
提示:
2 <= nums.length <= 1051 <= nums[i] <= 106
哈希 + 枚举
class Solution {public int minOperations(int[] nums) {Map<Integer, Integer> map = new HashMap<>();for(int num : nums){map.merge(num, 1, Integer::sum);}int res = 0;for(Map.Entry<Integer, Integer> entry : map.entrySet()){int cnt = entry.getValue();if(cnt == 1) return -1;res += cnt / 3;cnt %= 3;if(cnt != 0) res += 1;}return res;}
}
2871. 将数组分割成最多数目的子数组
中等
给你一个只包含 非负 整数的数组 nums 。
我们定义满足 l <= r 的子数组 nums[l..r] 的分数为 nums[l] AND nums[l + 1] AND ... AND nums[r] ,其中 AND 是按位与运算。
请你将数组分割成一个或者更多子数组,满足:
- 每个 元素都 只 属于一个子数组。
- 子数组分数之和尽可能 小 。
请你在满足以上要求的条件下,返回 最多 可以得到多少个子数组。
一个 子数组 是一个数组中一段连续的元素。
示例 1:
输入:nums = [1,0,2,0,1,2]
输出:3
解释:我们可以将数组分割成以下子数组:
- [1,0] 。子数组分数为 1 AND 0 = 0 。
- [2,0] 。子数组分数为 2 AND 0 = 0 。
- [1,2] 。子数组分数为 1 AND 2 = 0 。
分数之和为 0 + 0 + 0 = 0 ,是我们可以得到的最小分数之和。
在分数之和为 0 的前提下,最多可以将数组分割成 3 个子数组。所以返回 3 。
示例 2:
输入:nums = [5,7,1,3]
输出:1
解释:我们可以将数组分割成一个子数组:[5,7,1,3] ,分数为 1 ,这是可以得到的最小总分数。
在总分数为 1 的前提下,最多可以将数组分割成 1 个子数组。所以返回 1 。
提示:
1 <= nums.length <= 1050 <= nums[i] <= 106
AND 位运算性质
https://leetcode.cn/problems/split-array-into-maximum-number-of-subarrays/solutions/2464645/li-yong-and-xing-zhi-yi-ci-bian-li-pytho-p3bj/
class Solution {/**1. 先满足分数之和尽可能小结论:随着 AND 的数量越来越多,AND 的结果只会越来越小随着 OR 的数量越来越多,OR 的结果只会越来越大==> 假设 整个数组的 AND 记作 a > 0如果分出两个子数组 >= 2*a > a,此时只能分出一个数组,即 nums==>最小的分数之和为 nums 的 AND 结果2. 再满足分出的子数组尽量多*/public int maxSubarrays(int[] nums) {int ans = 0;int a = -1; // -1 就是 111...1,和任何数 AND 都等于那个数for(int x : nums){a &= x;if(a == 0){ans++;a = -1;}}return Math.max(ans, 1); // 如果 ans=0 说明所有数的 and>0,答案为 1}
}
2872. 可以被 K 整除连通块的最大数目
困难
给你一棵 n 个节点的无向树,节点编号为 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。
同时给你一个下标从 0 开始长度为 n 的整数数组 values ,其中 values[i] 是第 i 个节点的 值 。再给你一个整数 k 。
你可以从树中删除一些边,也可以一条边也不删,得到若干连通块。一个 连通块的值 定义为连通块中所有节点值之和。如果所有连通块的值都可以被 k 整除,那么我们说这是一个 合法分割 。
请你返回所有合法分割中,连通块数目的最大值 。
示例 1:
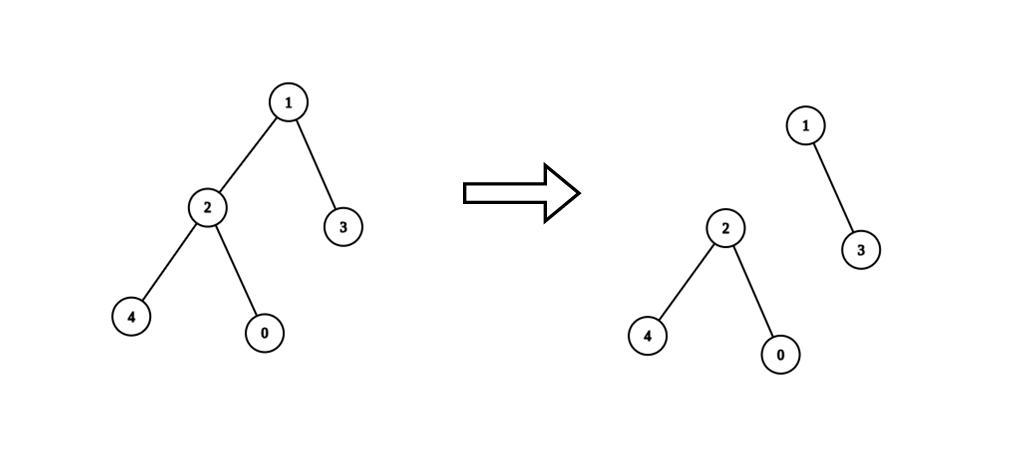
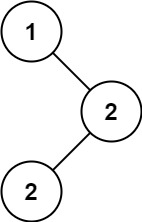
输入:n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6
输出:2
解释:我们删除节点 1 和 2 之间的边。这是一个合法分割,因为:
- 节点 1 和 3 所在连通块的值为 values[1] + values[3] = 12 。
- 节点 0 ,2 和 4 所在连通块的值为 values[0] + values[2] + values[4] = 6 。
最多可以得到 2 个连通块的合法分割。
示例 2:
输入:n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3
输出:3
解释:我们删除节点 0 和 2 ,以及节点 0 和 1 之间的边。这是一个合法分割,因为:
- 节点 0 的连通块的值为 values[0] = 3 。
- 节点 2 ,5 和 6 所在连通块的值为 values[2] + values[5] + values[6] = 9 。
- 节点 1 ,3 和 4 的连通块的值为 values[1] + values[3] + values[4] = 6 。
最多可以得到 3 个连通块的合法分割。
提示:
1 <= n <= 3 * 104edges.length == n - 1edges[i].length == 20 <= ai, bi < nvalues.length == n0 <= values[i] <= 1091 <= k <= 109values之和可以被k整除。- 输入保证
edges是一棵无向树。
DFS
class Solution {/**什么样的边可以删除?删除一条边分成两个连通块,这两个连通块的点权之和是k的倍数values之和可以被k整除只需要保证其中一个连通块的点权之和是k的倍数这意味着从任意一个点出发,计算出的答案都是一样的 */private List<Integer>[] g;private int[] values;private int k, ans;public int maxKDivisibleComponents(int n, int[][] edges, int[] values, int k) {g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);g[y].add(x);}this.values = values;this.k = k;dfs(0, -1);return ans;}public long dfs(int x, int fa){long sum = values[x];for(int y : g[x]){if(y != fa){sum += dfs(y, x);}}ans += sum % k == 0 ? 1 : 0;return sum;}
}
![[天翼杯 2021]esay_eval - RCE(disabled_function绕过||AS_Redis绕过)+反序列化(大小写wakeup绕过)](https://img-blog.csdnimg.cn/5bb974fa9f004da98079e22d539c53c5.png#pic_center)