点进去这篇文章的开源地址,才发现这篇文章和DC DSA居然是一个作者,数据浓缩写了三篇论文,第一篇梯度匹配,第二篇数据增强后梯度匹配,第三篇匹配数据分布。DC是匹配浓缩数据和原始数据训练一次后的梯度差,DSA是在DC前加入了一层数据增强,DM直接就匹配浓缩数据和原始数据丢入模型得到的输出,匹配输出的分布。
一个github地址包含了三个数据浓缩方法的开源代码。
1. 基于分布匹配的数据集浓缩
在降低训练成本方面,最近一个很有前途的方向是数据集凝聚,其目的是在保留原始信息的情况下,用一个小得多的学习合成集取代原来的大训练集。
虽然在小集合的压缩图像上训练深度模型可以非常快,但由于复杂的双层优化和二阶导数计算,它们的合成仍然是计算昂贵的(DD,DC,DSA)。
在本工作中,我们提出了一种简单而有效的方法,通过匹配合成图像和原始训练图像在多个采样嵌入空间的特征分布来合成压缩图像。我们的方法显著降低了合成成本,同时实现了相当或更好的性能。
2. 方法
2.1 数据浓缩的问题:
现有的方法包括DD,DC和DSA等,他们的弊端在于时间复杂度太高,内层需要训练模型并更新浓缩数据集,外层还需要适应不同的 θ 0 \theta_0 θ0,实现起来需要三层循环,时间复杂度高。
2.2 分布匹配的数据浓缩
真实数据分布记为 P D P_{\mathcal{D}} PD。
我们将训练数据记为 x ∈ ℜ d \boldsymbol{x} \in \Re^d x∈ℜd ,并且可以被编码到一个低维空间,通过函数 ψ ϑ : ℜ d → ℜ d ′ \psi_{\vartheta}: \Re^d \rightarrow \Re^{d^{\prime}} ψϑ:ℜd→ℜd′ ,其中 d ′ ≪ d d^{\prime} \ll d d′≪d , ϑ \vartheta ϑ 是函数的参数数值。 换句话说,每个embedding 函数 ψ \psi ψ可以被视为提供其输入的部分解释,而它们的组合则提供完整的解释。
现在我们可以使用常用的最大平均差异(MMD)来估计真实数据分布和合成数据分布之间的距离:
sup ∥ ψ ϑ ∥ H ≤ 1 ( E [ ψ ϑ ( T ) ] − E [ ψ ϑ ( S ) ] ) \sup _{\left\|\psi_{\vartheta}\right\|_{\mathcal{H}} \leq 1}\left(\mathbb{E}\left[\psi_{\vartheta}(\mathcal{T})\right]-\mathbb{E}\left[\psi_{\vartheta}(\mathcal{S})\right]\right) ∥ψϑ∥H≤1sup(E[ψϑ(T)]−E[ψϑ(S)])
由于我们无法获得真实数据分布,因此我们使用 MMD 的经验估计:
E ϑ ∼ P ϑ ∥ 1 ∣ T ∣ ∑ i = 1 ∣ T ∣ ψ ϑ ( x i ) − 1 ∣ S ∣ ∑ j = 1 ∣ S ∣ ψ ϑ ( s j ) ∥ 2 \mathbb{E}_{\boldsymbol{\vartheta} \sim P_{\vartheta}}\left\|\frac{1}{|\mathcal{T}|} \sum_{i=1}^{|\mathcal{T}|} \psi_{\boldsymbol{\vartheta}}\left(\boldsymbol{x}_i\right)-\frac{1}{|\mathcal{S}|} \sum_{j=1}^{|\mathcal{S}|} \psi_{\boldsymbol{\vartheta}}\left(\boldsymbol{s}_j\right)\right\|^2 Eϑ∼Pϑ ∣T∣1i=1∑∣T∣ψϑ(xi)−∣S∣1j=1∑∣S∣ψϑ(sj) 2
就是在不同参数取值的embedding函数下,输入原始数据和浓缩数据得到的输出要尽可能接近,论文里就直接使用了神经网络的输出,让神经网络的输出尽可能接近。
因为这篇论文是DSA的后续作,所以顺其自然,沿用了DSA的方法,训练的时候对浓缩数据和原始数据都进行了相同的数据增强。
min S E ω ∼ P ϑ ω ∼ Ω ∥ 1 ∣ T ∣ ∑ i = 1 ∣ T ∣ ψ ϑ ( A ( x i , ω ) ) − 1 ∣ S ∣ ∑ j = 1 ∣ S ∣ ψ ϑ ( A ( s j , ω ) ) ∥ 2 \min _{\mathcal{S}} \mathbb{E}_{\substack{\boldsymbol{\omega} \sim P_{\boldsymbol{\vartheta}} \\ \omega \sim \Omega}}\left\|\frac{1}{|\mathcal{T}|} \sum_{i=1}^{|\mathcal{T}|} \psi_{\boldsymbol{\vartheta}}\left(\mathcal{A}\left(\boldsymbol{x}_i, \omega\right)\right)-\frac{1}{|\mathcal{S}|} \sum_{j=1}^{|\mathcal{S}|} \psi_{\boldsymbol{\vartheta}}\left(\mathcal{A}\left(\boldsymbol{s}_j, \omega\right)\right)\right\|^2 SminEω∼Pϑω∼Ω ∣T∣1i=1∑∣T∣ψϑ(A(xi,ω))−∣S∣1j=1∑∣S∣ψϑ(A(sj,ω)) 2
A \mathcal{A} A就是对应的数据增强操作, ω \omega ω是对应数据增强操作的参数。
2.3 训练步骤

训练K-1步,每一步都选定一个embedding函数的参数,不断地训练并修改S使得S输出尽可能接近原始数据集T。(这个embedding函数就是一个具体的神经网络)
3. 结果
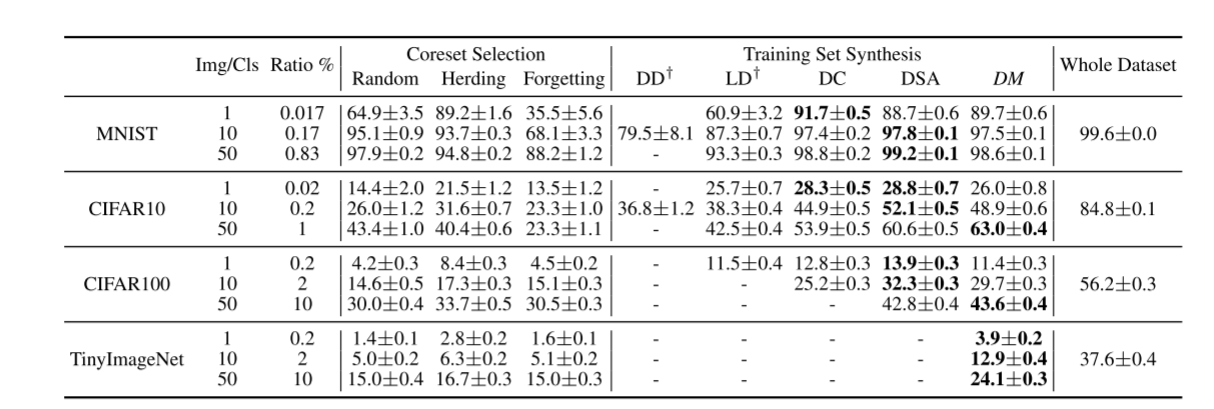
由于此方法计算不需要计算梯度,只需要正向传播embedding网络,得到输出之后反向传播浓缩数据集S即可,因此可以压缩到更多数量的图片上,并且第一次在TinyImageNet这种大数据集上进行压缩。
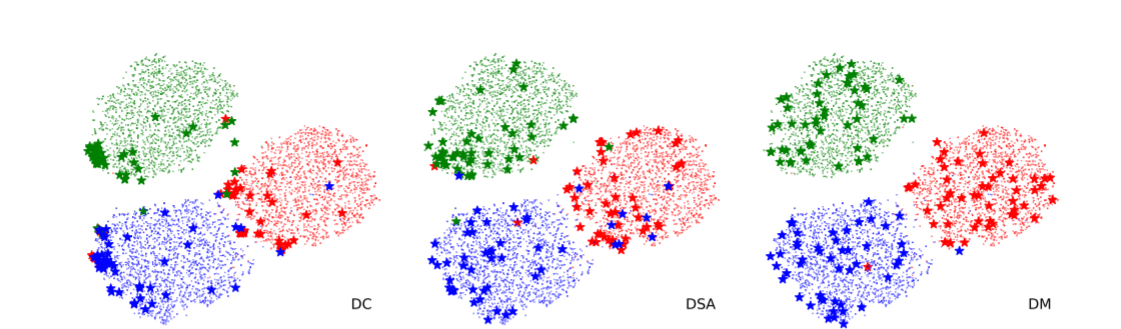
比起DC和DSA,DM得到的数据分布更接近原始数据分布。


](https://img-blog.csdnimg.cn/34f25434e13641d3a138f929d859c0fc.png)