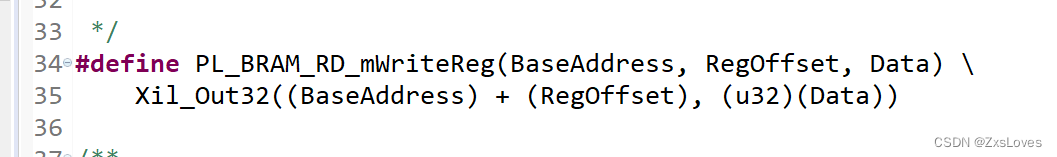前言

位图与布隆过滤器是用来在海量数据中判断一个数据在不在的问题的数据结构，这种数据结构在存储空间上大大的优于红黑树、哈希等数据结构

位图

我们为了处理一个数据在海量数据中在不在，那么我们的结果只有在与不在，我们令在为1，不在为0，也就是说对于每一个数据，我们只需要存储两个值，那么一个数据只需要一个bit位就够了

场景演示

比如这里我就有一个大小为21的位图，默认存储0，也就是没有数据，如果我们来了三个数据：2 7 19，那么位图就变成了下图

也就是把对应位映射成了1，表示对应位存在了数据，如果我们想要让数据消失，就只需要把对应位的内容映射为0即可

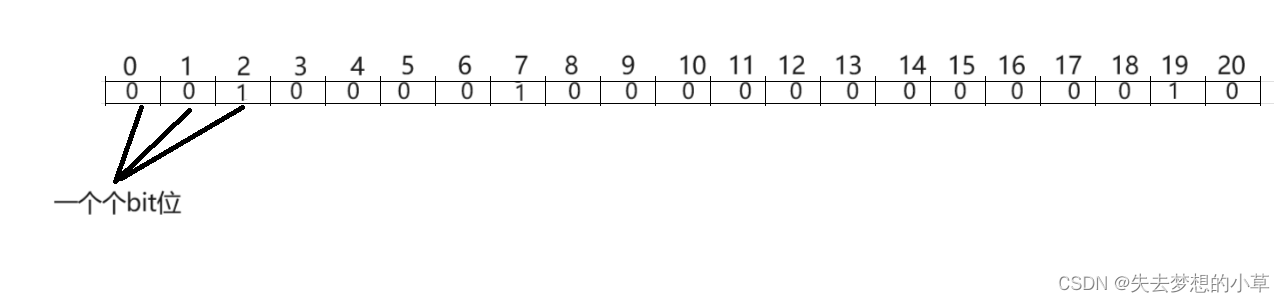
这里还需要注意一点：这里上面图的画是逻辑上的位图，不是物理内存存储的位图，因为物理内存会涉及到大小端的问题，也就是小端：低地址存低字节序，高地址存高字节序；大端：低地址存高字节序，高地址存低字节序。但是我们在使用位图是，只需要通过逻辑位图来理解即可，编译器会帮我们做好物理空间上的存储问题

应用场景

1. 快速查找某个数据是否在一个集合中
2. 去重并排序（位图大多数情况是用来处理在不在，如果已经在了，体现不出多个相同数据

//打印这些排序后的数据，实际的数据就是位图的下标，比特位表示的是在不在
for(int i = 0; i < N; i++) 
{if(bs.test(i)){cout << i << ' '; }
}

3. 求两个集合的交集、并集等

//bs1是集合一的位图，bs2是集合二的位图
for(int i = 0; i < N; i++)
{//交集if(bs1.test(i) && bs2.test(i)){cout << i << " ";}
}for(int i = 0; i < N; i++)
{//并集if(bs1.test(i) || bs2.test(i)){cout << i << " ";}
}

模拟实现

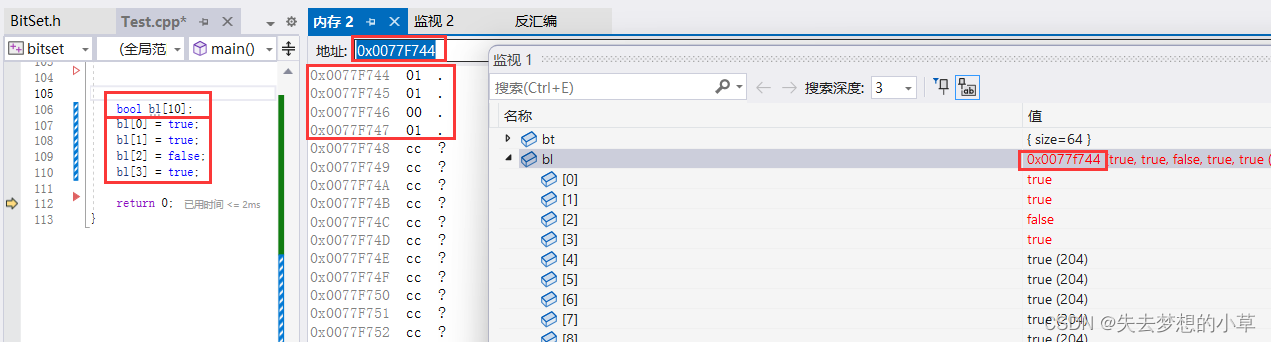
我们的内置类型有int，char，float，double没有专门针对于位做操作的类型，当然这里会有人说bool类型，bool经过测试，每个bool变量，还是占了1个字节，也就是8个比特位

所以我们通常是通过int或者char用模运算和除运算来确定数据对应的比特位，我们下面使用int来模拟实现位图

位图通常的需求有三个：set() reset() test() 这三个函数的意义分别为：对应比特位映射为1，表示数据存在、对应比特位映射为0，表述数据不存在，查找对应比特位是否存在，所有的int数据都用vector来存储，注释即为代码解释，请自行阅读代码

//N为非类型模板参数，N表示的需要使用的位的个数，也就是我们这张位图能够存储的数据的范围 —— [0, N)
template<size_t N>
class bitset
{
public:bitset(){//计算出需要开辟的vector空间大小,也可以N >> 5 + 1来计算 - 右移相当于 /2//当然对于负数的右移，就不是简单的是/2的问题了，有些编译器是逻辑右移，有些编译器是算术右移，没有完全统一size_t size = N / 32 + 1;//比如N = 35，也就是需要35个比特位，N/32==1，空间不够，需要+1， 其实更节省空间的说法是 - N/32向上取整_a.resize(size, 0);}// 数据num映射的那个标记成1void set(size_t num){size_t index = num / 32;//num >> 5;size_t right_count = num % 32;_a[index] |= (1 << right_count);}// num映射的那个标记成0void reset(size_t num){size_t index = num / 32;size_t right_count = num % 32;_a[index] &= (~(1 << right_count));//右移然后取反，使得x映射的那个位一定在&后变成0，其他位的0、1结果完全与原始的0、1一致}// 测试num映射位置是0还是1bool test(size_t num){size_t index = num / 32;size_t right_count = num % 32;return _a[index] & (1 << right_count);//_a[index]中的第right_count位是0是1,是1就是true，是0就是false}private:vector<int> _a;//用一个vector来存储位图
};

完成了基础版的位图的模拟实现，此时我们就能够用一个int大小的数据去存储[0, 32)这32个数据，位图的N的大小越大，存储的数据范围越广

问题

可能有些读者会有疑惑，这种映射关系是否只能针对正整数？是否能够处理字符串？
对于负数，我们有两种处理方法
方法一：先遍历数据，找到最小的负数MIN，然后整体的数据加上这个MIN的绝对值，然后放到位图中，在后序查询时只需要把查询的数加上MIN进行查询即可，不过这种方法有致命缺陷，如果又插入了一个更小的负数，那么位图中的表示全部都乱了

方法二：用两张位图存储，第一张位图存储正数，第二张位图存储负数，具体操作就是遍历所有数据，如果是正数和零，放入第一张位图，如果是负数，取绝对值放入第二张位图，查询时判断正负，然后分别去对应的位图中寻找即可

方法三：遍历数据，找到两个最值MAX和MIN，我们开辟位图时开辟的大小变成MAX + MIN，每一个负数都取绝对值 + MAX，然后把结果放到位图中，在查询时，如果查询数小于0，就查询 查询数的绝对值 + MAX的结果对应的位图上是0还是1，如果查询数大于等于0，小于等于MAX，就正常查询，如果大于MAX，就直接return false;

方法三中，比如下图中，-1，绝对值 + MAX = 9，所以位图中的9位置为1，|-4| + MAX = 12，所以位图中的12位置为1

方法二、三是比较推荐的

对于字符串的处理，所有的字符，不管是中文英文，都是有对应编码的，比如ASCII码，Unicode的UTF-8、UTF-16，也就是说，这些字符串都可以转换成整形，不过这里就会有个问题，不同的字符串，转换成整形是有可能相同的，也就是发生冲突，所以为了降低这种相同的可能性，前人设计了很多种字符串哈希算法，这里给了一个字符串哈希算法的网址：https://www.cnblogs.com/-clq/archieve/2012/05/31/2528153.html，可以自行了解阅读，简单来说，我们的字符串，通过字符串哈希算法的处理，都能够变成一个整形，然后放到位图中

不过这种方法在实际中还是有不少冲突的问题，所以就有了布隆过滤器，来降低冲突问题

例题

1、给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中？
40亿不重复的无符号整数，如果是在32位机上，无符号整数是4个字节，也就是总共160亿字节的数据，如果用set处理，其底层是红黑树，除了这些数据key，还需要存储，left、right、parent、colour，这些也都是4字节的，那么总共下来就是160 * 5 = 800亿字节的数据

1G = 2^10MB = 2^20KB = 2^30Byte，2^30字节就是10亿字节，也就是说：1G等于10亿字节，那么上面这道题如果用set存储，那么就需要80个G，想想就可怕是吧，内存就只有8个G，16个G，真要set处理，那只能分成小文件处理，后面会有其他题具体讲解此方法。

所以这里最好就用位图来处理，这40亿的不重复数据，也就是至少需要40亿的位图大小，但是我们并不知道最大的数据是多少，所以直接给一个顶配的位图，直接把无符号数覆盖满，也就是给一个2^32个比特空间大小的位图，也就是2^29个字节大小的位图，1G = 2^30字节，也就是说这个位图的大小为500MB，这个大小我们就能够承受，这个数据量大多数电脑就能够轻松拿捏了，对于template< size_t N >这个N的设置有多种方式，bitset< 0xFFFFFFFF > bitset< -1 >都可，只不过需要注意的是，库中提供的bitset给了很多限制，怕我们乱开空间，我们可以用自己写的位图来开辟这么大的空间处理问题

2、给定100亿个整数，设计算法找到只出现一次的整数
有两个方法：
方法一：我们的位图每一个位只能存储在不在，我们修改位图的存储结构 —— 每两个比特位，存储一个数据的信息，此时我们对于一个数据，就能够存储四种信息，比如我们可以规定：00 - 没有数据， 01 - 有一个数据，10 - 有两个以上的数据

比如上面这个修改后的位图，存储的信息如下：1个0，多个1，多个2，0个3，多个4，1个5，1个6，0个7
这张位图的实现上需要修改的就是，查询、插入整数num时对应操作的比特位需要×2，此时对应的比特位，才是存储信息的第一位，下一位就是第二位，我们在操控信息时，也就是处理：_a[num * 2 / 32]里的1 << (num * 2 % 32) 1 << ((num * 2 % 32) + 1)，因为int的bit位是偶数，所以(num % 32)并不会因为 + 1跑到下一个int中

方法二：用两张位图处理，两张位图的相同位置一起组成两个位，同样也是00 - 该没有数据， 01 - 有一个数据，10 - 有两个以上的数据，这样的存储模式，这就可以不用修改位图了，只需要封装一个针对这个题的新位图

template<size_t N>
class twicebitset
{
public:void set(size_t num){//_bt1 _bt2//  0   0    ->该bit位没有值//  0   1    ->该bit位有一个值//  1   0    ->该bit位有两个及以上个值if (!_bt1.test(num) && !_bt2.test(num))//如果bt1和bt2的num的位为0，那么这里会进去{_bt2.set(num);//设置num位}else if (!_bt1.test(num) && _bt2.test(num))// 01 会进去{_bt1.set(num);_bt2.reset(num);}else//10不会处理，不会有11的情况{;}}void reset(size_t num){_bt1.reset(num);_bt2.reset(num);}bool is_once(size_t num){return !_bt1.test(num) && _bt2.test(num);//01 -> 唯一值}private:bitset<N> _bt1;//高位bitbitset<N> _bt2;//低位bit
};

3、给两个文件，分别有100亿个整数，我们只有1G内存，如何找到这两个文件的交集？
我们这里需要明确，这种海量数据的情况下位图所开大小和数据量无关，只与数据类型有关，这100亿数据中必定会有重复数据，这些都是整数，直接开bitset< -1 >大小的位图空间就可以了，也就是大概500MB左右，读入第一个文件的数据到位图中，另一个文件的数据在位图中寻找，寻找的结果放到unordered_set< int >容器中，因为可能存在重复值，用set容器去重，并且用unordered效率更高一些，除此之外，这100亿个在文件中的整数，并不是一次性放到内存中处理，而且分批次放到内存中处理，比如一次处理1亿个整数，也就是250MB 这样就能够在1G内存来处理这些数据

布隆过滤器

上面我们讲到了一个例子，是通过哈希函数把字符串转成整形，这种方式是有可能出现两个不同的字符串映射到同一个整形，导致误判的，所以就使用到了布隆过滤器，来降低这种误判的风险

布隆过滤器是一种概率性的数据结构，是对一个字符串使用多个哈希函数，在位图中映射到多个位置，当在检测在不在的时候，只有被检测的字符串在多个哈希函数的处理下，都完全映射到位图中被映射过的位置，此时才能判断出，被检测字符串在位图中。

例子理解

下图即是：百度、腾讯、阿里，通过三个哈希函数，映射到了位图中

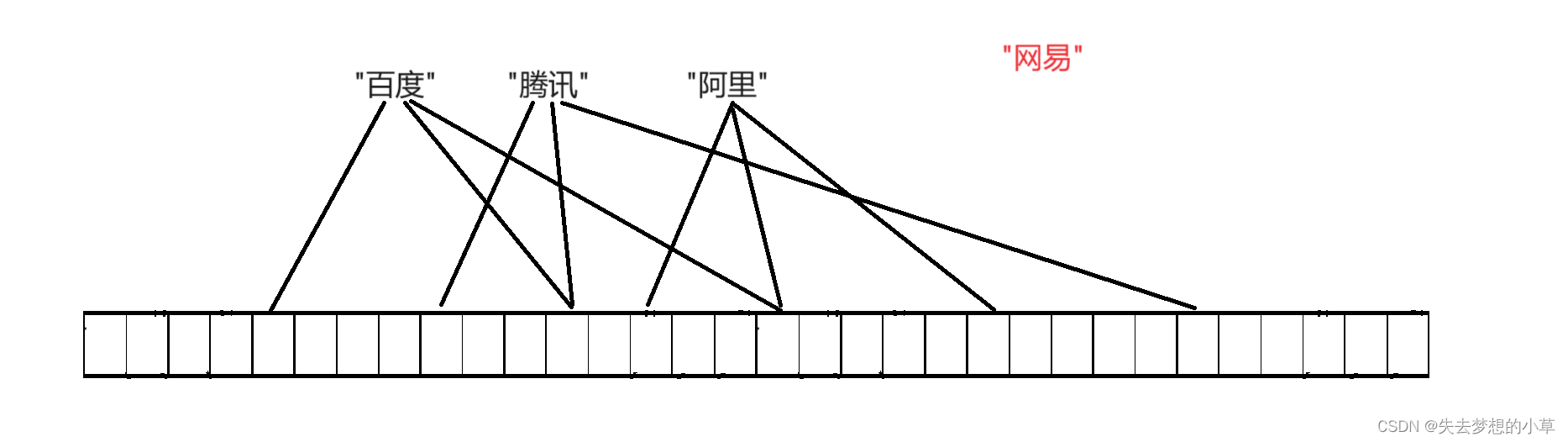
然后来了一个网易
1、如果网易通过相同的三个哈希函数，映射到了下图位置中

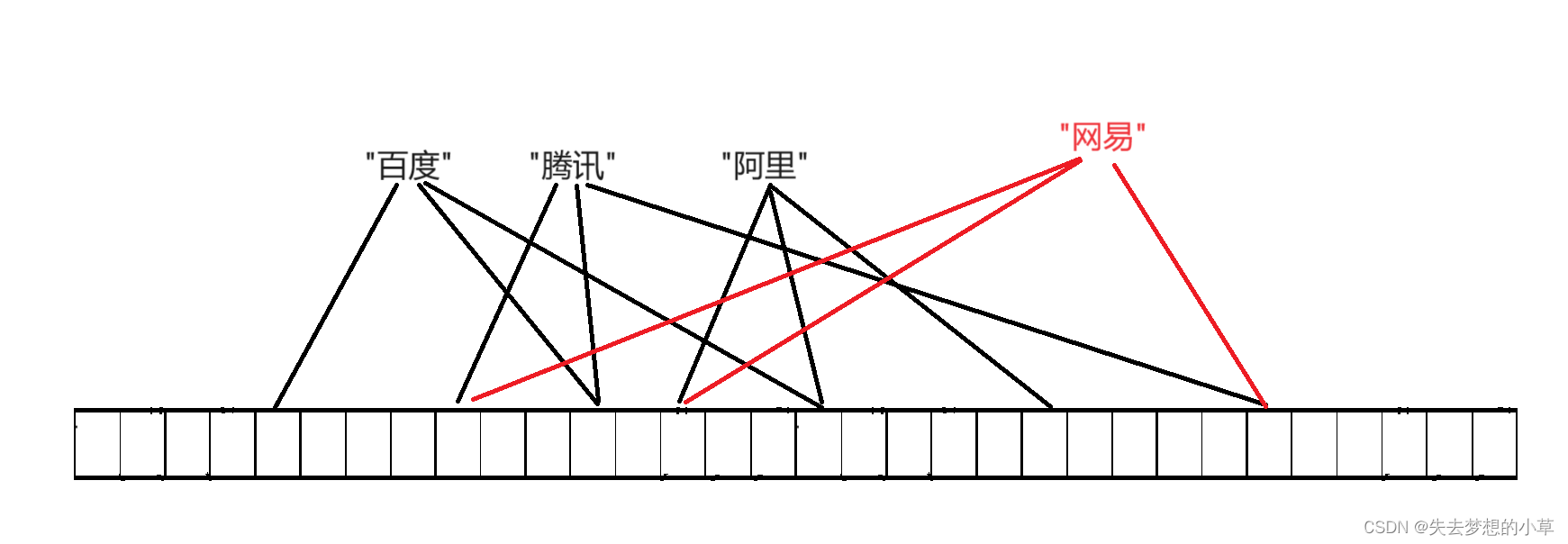
也就是通过布隆过滤器，发现网易是在位图中的，也就发生了误判，这是一种情况，也是我们不想看到的情况

2、如果映射成了：

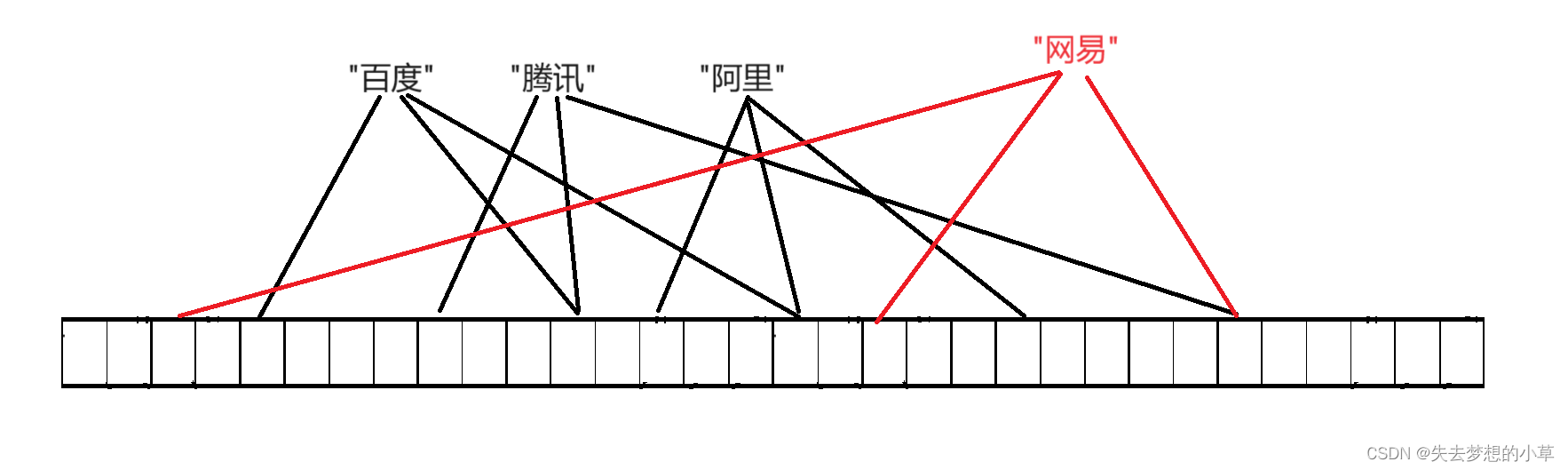
也就是网易通过三个哈希，映射到了位图中为0的位置，此时就判断，网易一定不在位图中，这个判断是一定正确的

有人会说，这样有没有可能比单个哈希函数的误判率更高？
我认为，如果位图开的过小，是有可能的，因为存储大量的值后，可能位图都快满了，怎么检测，都是1，但是，在实际中，位图开的空间是很大的，始终让位图保持在一个稀疏状态，在存储阶段，像百度和腾讯通过哈希函数映射到相同的位图位置的概率会很小，检测阶段，被检测字符串能够通过多个哈希函数映射到都为1的位置概率也会变的很小

//N表示的需要使用的位的个数，也就是我们这张位图能够存储的整形范围 —— [0, N)
template<size_t N>
class bitset
{
public:bitset(){//计算出需要开辟的vector空间大小,也可以N >> 5 + 1来计算 - 右移相当于 /2//当然对于负数的右移，就不是简单的是/2的问题了，有些编译器是逻辑右移，有些编译器是算术右移，没有完全统一size_t size = N / 32 + 1;//比如N = 35，也就是需要35个比特位，N/32==1，空间不够，需要+1， 其实更节省空间的说法是 - N/32向上取整_a.resize(size, 0);}// 数据num映射的那个标记成1void set(size_t num){size_t index = num / 32;//num >> 5;size_t right_count = num % 32;_a[index] |= (1 << right_count);}// num映射的那个标记成0void reset(size_t num){size_t index = num / 32;size_t right_count = num % 32;_a[index] &= (~(1 << right_count));//右移然后取反，使得x映射的那个位一定在&后变成0，其他位的0、1结果完全与原始的0、1一致}// 测试num映射位置是0还是1bool test(size_t num){size_t index = num / 32;size_t right_count = num % 32;return _a[index] & (1 << right_count);//_a[index]中的第right_count位是0是1,是1就是true，是0就是false}
private:vector<int> _a;//用一个vector来存储位图
};template<size_t N>
class BloomFilter
{
private:size_t BKDRHash(const string& str){size_t hash = 0;size_t i = 0;int ch = 0;while (ch = str[++i]){hash = hash * 131 + ch;   }return hash;}size_t SDBMHash(const string& str){size_t hash = 0;size_t i = 0;int ch = 0;while (ch = str[++i]){hash = 65599 * hash + ch;//hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;  }return hash;}size_t RSHash(const string& str){size_t hash = 0;size_t magic = 63689;size_t i = 0;int ch = 0;while (ch = str[++i]){hash = hash * magic + ch;magic *= 378551;}return hash;}public:void set(const string& str){_bt.set(BKDRHash(str) % N);_bt.set(SDBMHash(str) % N);_bt.set(RSHash(str) % N);}//void reset();//不能有reset，因为一个位图位置，不一定属于那一个人bool test(const string& str){return _bt.test(BKDRHash(str) % N) && _bt.test(SDBMHash(str) % N) && _bt.test(RSHash(str) % N);}private:bitset<N> _bt;
};

应用

通过前面的例子，需要知晓的，布隆过滤器对于判断不在是完全准确的，对于判断在是不准确的
所以应用场景应该是针对不要求完全准确的场景，比如快速判断昵称是否被注册过？如果没有被注册过，就能进行后序操作，如果注册过，就让用户更换昵称，这里的逻辑就比较符合布隆过滤器，昵称没有被注册过，对应的就是通过布隆过滤器检测为不在，这是准确的，而对于昵称存在，让用户更换昵称，这个不是准确的（新昵称指向了位图中的三个标注为1的位图位置，但是这个昵称并没有被用过），但是没有关系，反正用户不知道，所以这里就要求，布隆过滤器的误判率需要小于5%？3%？这是根据需求来说的。

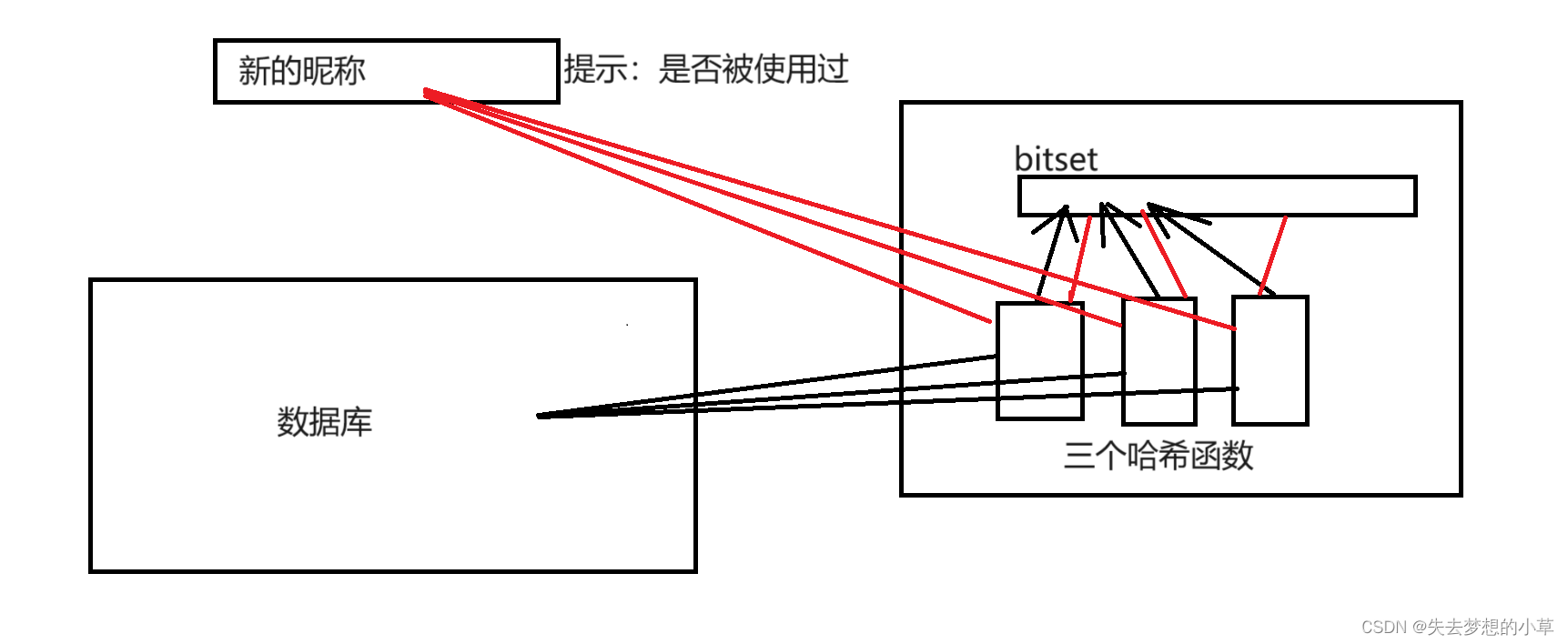
当然这种场景也能够做到精准，只不过会牺牲一定的效率，我们的所有数据还是首先通过布隆过滤器进行判断，如果是没有被注册过，这是准确的，不用管别的了，如果是被注册过，就去数据库中寻找，如果找到了，提示：该昵称被注册过了，如果没找到，那么也就是没有被注册过，提示：改昵称没有被注册过

简单来说：降低数据库的查询负载压力，提高效率

除了上面的应用还有利用布隆过滤器减少磁盘IO或者网络请求，一旦一个值必定不存在，我们就可以不用进行后续消耗较大的查询请求

例题

1、给定两个文件，分别有100亿个query（查询），只有1G内存，如何找到两个文件的交集？精确算法和近似算法
query是查询，一般是针对数据库中的信息进行查询，比如查询字符串，假设查询的字符串平均长度是30byte，那么这里就是3000Byte，也就是300G的数据量（10亿Byte = 1G）
因为内存一般只有8G、16G，和位图的例题部分的第三个问题相同，也需要把这100亿个查询，分成多个小文件，比如分成1000个小文件，那么最简单的思路就是，第一个文件中的一个小文件分别与另一个文件中的1000个小文件进行比较，找出这一个小文件与第二个文件的交集，这么做1000次，然后进行去重，结果就是这两个文件的交集，总共会有1000 * 1000次小文件之间的比较

但是，这种方式的效率非常低，有很多重复动作，所以，我们需要进行改进，这1000个小文件，我们可以进行预处理 —— 哈希切分
我们使用一个哈希函数，去处理query字符串，然后 % 1000，( i = hash_fun(query) % 1000; // i是小文件编号 )其结果就被映射到了i ∈ [0, 1000)，然后我们就把这个query放到对应的小文件中，这样我们把两个文件处理成了2000个小文件，比如：第一个文件中的i ==0的小文件和第二个文件中i == 0的文件找交集，第一个文件的i == 4的和第二个文件i == 4找交集，这样得到的结果再进行去重，去重后的就是我们需要的结果（两个文件中相同的query，一定会经过哈希函数 和 % 1000之后，分别进入两个对应的小文件，我们只需要对应的小文件进行查找，有一点点哈希桶的味道，相同特点的数据进入一个桶中，只需要在这个桶里查询值），总共会有1000次小文件之间的比较，大幅度的提高了效率

这300G的文件的读取是一部分一部分读取，把一些query数据放到缓冲区中（把磁盘一个扇区的数据读到缓冲区），然后把缓冲区中的数据读取到出来进行处理，处理完后马上就写入到对应的小文件中去，所以预处理这300G的文件是不需要消耗太多的内存的，主要的消耗是IO消耗，即读写的消耗，以及会有一些CPU的消耗。CPU密集型也就是计算密集性，IO密集性也就是读写密集性，这里是IO密集性

这里需要注意，缓冲区是内存与外设进行交换时的一块内存区域，而缓存命中这个概念的缓存是CPU高速缓存，不是内存中的缓存

但是，这里还有问题，如果大量的query字符串预处理阶段，都进入了同一个小文件（i = hash_fun(query) % 1000; 处理后某个 i 下的query过多，“桶太长”），就会导致小文件过大，超过800MB，1G …
小文件过大的来源有二：
一：有大量的重复query
二：大量的不同字符串通过hash %1000，得到相同的 i （发生冲突）

对于情况二，比较好处理，可以更换hash函数，再切分
对于情况一：换hash函数没有作用，都还是会进入同一个小文件

我们是不知道是情况一还是情况二的
所以真正的解决方案：还是先把小文件的query读到内存中的一个数据容器中（set、unordered_set)，如果insert时，报错抛bad_alloc异常，那么说明是情况一，此时就换一个哈希函数，再进行哈希切分；如果能够正常全部读到数据容器中，说明是情况一或者就是普通的小文件，这个小文件就处理完成了，只需要接着对另一个文件中的对应小文件进行读入数据容器

对于上面两个小文件的精确算法，就使用set数据容器，而对于近似算法，就还是使用布隆过滤器

思考：布隆过滤器是否支持删除操作？
不支持，因为一个布隆过滤器中的一个位，可能同时是"阿里巴巴"和"百度"通过哈希函数映射过去的，所以，我们针对阿里巴巴的删除操作，就会影响到百度，所以不支持

2、给一个超过100G大小的log file，log中存IP地址，设计算法，找到出现次数最多的IP？那出现次数最多的K个IP地址呢？
第一步同样，先用哈希切分，把这100多个G的log file切分成500个，1000个小文件，大概平均一份就是100MB，200MB，当然这里还是会出现问题一中的问题，还是相同的解决办法，这里就不赘述了

这里每个小文件中都有一些重复的IP，我们就是要从这几百个小文件中找到最大的那一个，那么我们就用map分别统计每个小文件中每个IP出现的次数，并用一个pair<string, int>变量不断更新记录各个每个小文件中的出现次数最多的IP

对于出现次数最多的K个IP地址，就使用priority_queue数据结构，建一个大小为K的小堆，先随便放入K个数据，然后让每个小文件中的数据和堆顶数据进行比较，如果堆顶数据小于外部数据，那么堆顶数据pop掉，外部数据入堆，这么扫过所有小文件，最后堆中的数据就是最后的结果

3、如何扩展布隆过滤器使得它支持删除操作呢？
要完成删除操作，就需要进行计数，计数将不可避免的会消耗一定的空间
具体的操作方式是，原来我们对于每一个bit位进行判断是否存在扩展为每四个bit位，每六个bit位，也就是将每一个位扩展为了一个小计数器，四位就允许冲突15次，六位就允许冲突63次，如果超出冲突次数，还是无法完成删除操作，所以为了保证完成删除操作，只能尽可能扩大位图大小，减少冲突可能性，所以删除操作是不稳定的，一般也不会要求布隆过滤器做删除操作。