leetCode 583.两个字符串的删除操作 动态规划 + 优化空间复杂度（二维dp、一维dp）

583. 两个字符串的删除操作 - 力扣（LeetCode）

给定两个单词 word1 和 word2 ，返回使得 word1 和  word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

示例  2:

输入：word1 = "leetcode", word2 = "etco"
输出：4

 一、递归搜索 + 保存计算结果 = 记忆化搜索

  • 二维memo数组 存储计算过的子问题的结果 
class Solution {
public:// 递归搜索 + 保存计算结果 = 记忆化搜索// 二维memo数组 存储过的子问题的结果int minDistance(string s, string t) {int m = s.size(),n = t.size(),memo[m][n]; // 二维memo数组 存储计算过的子问题的结果;memset(memo,-1,sizeof(memo));// -1 表示没有访问过function<int(int,int)> dfs = [&](int i,int j) -> int {if(i<0) //base case 当i指针越界，此时return j+1;if(j<0) //base casereturn i+1;if (memo[i][j] != -1) // memo中有当前遇到的子问题的解，直接拿来返回return memo[i][j];if (s[i] == t[j]) {  memo[i][j] = dfs(i-1, j-1);} else {// memo[i][j] = min(min(dfs(i-1, j)+1,dfs(i, j-1)+1),dfs(i-1, j-1)+2);// memo[i][j] = min(dfs(i-1, j)+1,dfs(i, j-1)+1);memo[i][j] = min(dfs(i-1, j),dfs(i, j-1))+1;}return memo[i][j];};return dfs(m-1,n-1);}
}

二、动态规划 与 递归 的区别 

  • 递归公式 
if (s[i] == t[j]) {  memo[i][j] = dfs(i-1, j-1);
} else {// memo[i][j] = min(min(dfs(i-1, j)+1,dfs(i, j-1)+1),dfs(i-1, j-1)+2);// memo[i][j] = min(dfs(i-1, j)+1,dfs(i, j-1)+1);memo[i][j] = min(dfs(i-1, j),dfs(i, j-1))+1;
}

递归是自上而下调用，子问题自下而上被解决，最后解决了整个问题，而dp是从base case 出发，通过在dp数组记录中间结果，自下而上地顺序地解决子问题

  • dp解法

1.确定dp数组（dp table）以及下标的含义

dp[i][j]:以i-1为结尾的字符串word1,和以j-1为结尾的字符串word2，想要达到相等，所需要删除元素的最少次数

2.确定递推公式

if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
}

3.dp数组初始化

从递推式可看出，dp[i][0] 和 dp[0][j] 是一定要初始化的

  • dp[i][0]:word2为字符串，以 i-1 为结尾的字符串 word1 需要删除 i 个元素才能变成空串，和word2相同
  • dp[0][j]:word1为字符串，以 j-1 为结尾的字符串 word2 需要删除 j 个元素才能变成空串，和word1相同
  • dp[0][0]=0,因为两个空字符串相同，删除操作为0
for(int i=1;i<=m;++i) dp[i][0] = i;
for(int j=1;j<=n;++j) dp[0][j] = j;

4.确定遍历顺序

从递推公式 dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1; 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据正上方、正左方推出来的，所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算。

5.举例推导dp数组

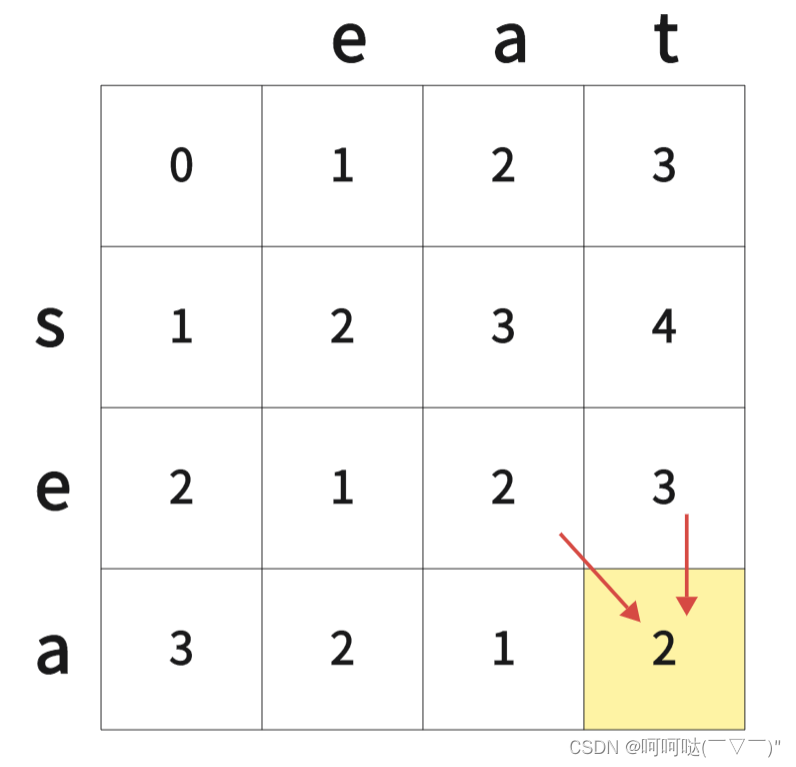
 （1）动态规划 二维dp

class Solution {
public:int minDistance(string word1, string word2) {int m = word1.size(),n = word2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;++i) dp[i][0] = i;for(int j=1;j<=n;++j) dp[0][j] = j;for(int i=1;i<=m;++i) {for(int j=1;j<=n;++j) {if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];// else dp[i][j] = min(min(dp[i-1][j]+1,dp[i][j-1]+1),dp[i-1][j-1]+2);else dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1);}}return dp[m][n];}
};
  • 时间复杂度: O(m * n)
  • 空间复杂度: O(m * n)

（2）动态规划 二维dp 优化空间 

class Solution {
public:  // 动态规划 二维dp 优化空间int minDistance(string word1, string word2) {int m = word1.size(),n = word2.size();// vector<vector<int>> dp(m+1,vector<int>(n+1));vector<vector<int>> dp(2,vector<int>(n+1));for(int j=1;j<=n;++j) dp[0][j] = j;for(int i=1;i<=m;++i) {dp[i%2][0] = i;for(int j=1;j<=n;++j) {if(word1[i-1] == word2[j-1]) dp[i % 2][j] = dp[(i-1)%2][j-1];else dp[i%2][j] = min(dp[(i-1)%2][j]+1,dp[i%2][j-1]+1);}}return dp[m%2][n];}
};
  • 时间复杂度: O(m * n)
  • 空间复杂度: O(n)

（3）动态规划 一维dp(滚动数组) 优化空间

class Solution {
public:  // 动态规划 一维dp(滚动数组) 优化空间int minDistance(string word1, string word2) {int m = word1.size(),n = word2.size();vector<int> dp(n+1);for(int j=1;j<=n;++j) dp[j] = j;for(int i=1;i<=m;++i) {// pre 代表dp[i-1][0]int pre = dp[0];// 初始化当前层的 dp[i][0]dp[0] = i;for(int j=1;j<=n;++j) {int tmp = dp[j];if(word1[i-1] == word2[j-1]) dp[j] = pre;else dp[j] = min(dp[j]+1,dp[j-1]+1);pre = tmp;}}return dp[n];}
};
  • 时间复杂度: O(m * n)
  • 空间复杂度: O(n)

本题除了这种解法外，还有这种解题思路：先求出最长公共子序列,然后 word1.size() + word2.size() - 两倍的最长公共子序列

求最长公共子序列，可以看我往期的这篇文章：leetCode 1143.最长公共子序列

（1）二维dp 

class Solution {
public: int minDistance(string word1, string word2) {int m = word1.size(),n = word2.size();vector<vector<int>> dp(m+1,vector<int>(n+1)); for(int i=1;i<=m;++i) {for(int j=1;j<=n;++j) {if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}return m + n - 2 * dp[m][n];}
};
  • 时间复杂度: O(m * n)
  • 空间复杂度: O(m * n)

（2）二维dp：优化空间 

class Solution {
public:  // 方法二 二维dp 优化空间int minDistance(string word1, string word2) {int m = word1.size(),n = word2.size();vector<vector<int>> dp(2,vector<int>(n+1)); for(int i=1;i<=m;++i) {for(int j=1;j<=n;++j) {if(word1[i-1] == word2[j-1]) dp[i%2][j] = dp[(i-1)%2][j-1] + 1;else dp[i%2][j] = max(dp[(i-1)%2][j],dp[i%2][j-1]);}}return m + n - 2 * dp[m%2][n];}
};
  • 时间复杂度: O(m * n)
  • 空间复杂度: O(n)

（3）一维dp：优化空间

class Solution {
public:// 方法二 一维dp 优化空间int minDistance(string word1, string word2) {int m = word1.size(),n = word2.size();vector<int> dp(n+1); for(int i=1;i<=m;++i) {int pre = dp[0];for(int j=1;j<=n;++j) {int tmp = dp[j];if(word1[i-1] == word2[j-1]) dp[j] = pre + 1;else dp[j] = max(dp[j],dp[j-1]);pre = tmp;}}return m + n - 2 * dp[n];}
};
  • 时间复杂度: O(m * n)
  • 空间复杂度: O(n)

参考和推荐文章、视频：

代码随想录 (programmercarl.com)

动态规划之子序列，还是为了编辑距离做铺垫 | LeetCode：583.两个字符串的删除操作_哔哩哔哩_bilibili

来自代码随想录课堂的截图：

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/157410.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

苹果CMS海螺模版V20修复版/加广告代码 ​适合视频影视类网站使用​

苹果CMS海螺模版V20修复版/加广告代码 ​适合视频影视类网站使用​

最新苹果CMS海螺模版V20修复版&#xff0c;增加广告代码&#xff0c;适合视频影视类网站使用&#xff0c;有兴趣的可以研究研究。 修复说明&#xff1a; 修复多线路时播放页列表点其他线路还是播放默认线路的问题 修复前台黑白切换和字体颜色切换失效 修复微信二维码没有对…
阅读更多...
c语言表达式求值--整型提升

c语言表达式求值--整型提升

什么是整型提升&#xff1f; C的整型算术运算总是至少以缺省整型类型的精度来进行的。 为了获得这个精度&#xff0c;表达式中的字符和短整型操作数在使用之前被转换为普通整型&#xff0c;这种转换称为整型提升。 什么叫缺省整数类型&#xff1f;缺省在计算机里面是默认的意…
阅读更多...
【数据结构】线段树

【数据结构】线段树

算法提高课笔记 还未更新完 文章目录 原理pushupbuildmodifyquerypushdown&#xff08;懒标记 / 延迟标记&#xff09;扫描线法 原理 时间复杂度&#xff1a;O(logn) 线段树是一棵二叉树&#xff0c;把一段区间分成多个部分 类似堆的方式&#xff0c;用一维数组存整棵树 对…
阅读更多...
计算机导论实验——Linux基础入门

计算机导论实验——Linux基础入门

使用Xshell登录 Linux 主机 linux命令&#xff1a; cd&#xff1a;去哪里 pwd&#xff1a;在哪里 ls&#xff1a;查看当前有什么文件 mkdir&#xff1a;创建新目录 cp&#xff1a;复制 cat&#xff1a;连接或显示文件 rm&#xff1a;删除 mv&#xff1a;用于移动或重命名文件…
阅读更多...
Android Studio版本升级后的问题 gradle降级、jdk升级

Android Studio版本升级后的问题 gradle降级、jdk升级

Cannot use TaskAction annotation on method IncrementalTask.taskAction$gradle_core() because interface org.gradle.api.tasks.incremental.IncrementalTaskInputs is not a valid parameter to an action method. 修改下面两处地方分别为7.0.3、7.3.3Android Gradle plu…
阅读更多...
Spark中的Driver、Executor、Stage、TaskSet、DAGScheduler等介绍

Spark中的Driver、Executor、Stage、TaskSet、DAGScheduler等介绍

工作流程&#xff1a; Driver 创建 SparkSession 并将应用程序转化为执行计划&#xff0c;将作业划分为多个 Stage&#xff0c;并创建相应的 TaskSet。Driver 将 TaskSet 发送给 TaskScheduler 进行调度和执行。TaskScheduler 根据资源情况将任务分发给可用的 Executor 进程执…
阅读更多...
基于 chinese-roberta-wwm-ext 微调训练中文命名实体识别任务

基于 chinese-roberta-wwm-ext 微调训练中文命名实体识别任务

一、模型和数据集介绍 1.1 预训练模型 chinese-roberta-wwm-ext 是基于 RoBERTa 架构下开发&#xff0c;其中 wwm 代表 Whole Word Masking&#xff0c;即对整个词进行掩码处理&#xff0c;通过这种方式&#xff0c;模型能够更好地理解上下文和语义关联&#xff0c;提高中文文…
阅读更多...
数据仓库Hive（林子雨课程慕课）

数据仓库Hive（林子雨课程慕课）

文章目录 9.数据仓库Hive9.1 数据仓库的概念9.2 Hive简介9.3 SQL语句转换为MapReduce作业的基本原理9.4 Impla9.4.1 Impala简介9.4.2 Impala系统架构9.4.3 Impala查询执行过程9.4.4 Impala与Hive的比较 9.5 Hive的安装和基本操作9.5.1 Hive安装9.5.2 Hive基本操作 9.数据仓库Hi…
阅读更多...
黑马点评-05缓存穿透问题及其解决方案,缓存空字符串或使用布隆过滤器

黑马点评-05缓存穿透问题及其解决方案,缓存空字符串或使用布隆过滤器

缓存穿透问题(缓存空) 缓存穿透的解决方案 缓存穿透(数据穿透缓存直击数据库): 缓存穿透是指客户端请求访问缓存中和数据库中都不存在的数据,此时缓存永远不会生效并且用户的请求都会打到数据库 数据库能够承载的并发不如Redis这么高&#xff0c;如果大量的请求同时访问这种…
阅读更多...
十大排序算法Java实现及时间复杂度

十大排序算法Java实现及时间复杂度

文章目录 十大排序算法选择排序冒泡排序插入排序希尔排序快速排序归并排序堆排序计数排序基数排序桶排序时间复杂度 参考资料 十大排序算法 选择排序 原理 从待排序的数据元素中找出最小或最大的一个元素&#xff0c;存放在序列的起始位置&#xff0c; 然后再从剩余的未排序元…
阅读更多...
C++类和对象（下）

C++类和对象（下）

目录 一、初始化列表 二、单参构造参数和explicit关键字 三、匿名对象 四、static成员 五、友元 六、内部类 一、初始化列表 之前我们在构造函数中写得还不错&#xff0c;也没发现什么问题&#xff0c;为什么C还有搞一个初始化列表呢&#xff1f; 如下这段代码&#x…
阅读更多...
mars3d的api文档关于addDynamicPosition查找使用说明

mars3d的api文档关于addDynamicPosition查找使用说明

示例链接&#xff1a;功能示例(Vue版) | Mars3D三维可视化平台 | 火星科技 api地址&#xff1a;Mars3D三维可视化平台 | 火星科技 说明&#xff1a; 1.用户反馈不知道如何搜索这个属性的用法 说明&#xff1a; 1. 示例代码中的graphic.addDynamicPosition()说明这个addDynam…
阅读更多...
基本微信小程序的二手车交易平台

基本微信小程序的二手车交易平台

项目介绍 首先,论文一开始便是清楚的论述了小程序的研究内容。其次,剖析系统需求分析,弄明白“做什么”,分析包括业务分析和业务流程的分析以及用例分析,更进一步明确系统的需求。然后在明白了小程序的需求基础上需要进一步地设计系统,主要包罗软件架构模式、整体功能模块、数…
阅读更多...
@MultipartConfig注解

@MultipartConfig注解

前言&#xff1a; 在学习Javaweb的Servlet文件上传和下载的过程中&#xff0c;我们会遇到一个特殊的注解---MultipartConfig。 MultipartConfig的适用情况&#xff1a; 1.文件上传: 当您的应用程序需要接收用户上传的文件时&#xff0c;可以在相应的 Servlet 上使用 Multipart…
阅读更多...
Jmeter连接mysql数据库详细步骤

Jmeter连接mysql数据库详细步骤

一、一般平常工作中使用jmeter 连接数据库的作用 主要包括&#xff1a; 1、本身对数据库进行测试&#xff08;功能、性能测试&#xff09;时会需要使用jmeter连接数据库 2、功能测试时&#xff0c;测试出来的结果需要和数据库中的数据进行对比是否正确一致。这时候可以通过j…
阅读更多...
C++ 位图与布隆过滤器

C++ 位图与布隆过滤器

目录 前言位图场景演示应用场景模拟实现问题例题 布隆过滤器例子理解应用 例题 前言 位图与布隆过滤器是用来在海量数据中判断一个数据在不在的问题的数据结构&#xff0c;这种数据结构在存储空间上大大的优于红黑树、哈希等数据结构 位图 我们为了处理一个数据在海量数据中…
阅读更多...
SQL开发笔记之专栏介绍

SQL开发笔记之专栏介绍

Sql是用于访问和处理数据库的标准计算机语言&#xff0c;使用SQL访问和处理数据系统中的数据&#xff0c;这类数据库包括&#xff1a;Mysql、PostgresSql、Oracle、Sybase、DB2等等&#xff0c;数据库无非围绕着“增删改查”的核心业务进行开发。并且目前绝大多数的后端程序开发…
阅读更多...
很烦的Node报错积累

很烦的Node报错积累

目录 1. 卡在sill idealTree buildDeps2、Node Sass老是安装不上的问题3、unable to resolve dependency tree4、nvm相关命令5、设置淘宝镜像等基操5.1 镜像 5.2 npm清理缓存6、Browserslist: caniuse-lite is outdated loader 1. 卡在sill idealTree buildDeps 参考&#xf…
阅读更多...
国际通用的Bug管理工具推荐：多款工具助力项目开发与管理

国际通用的Bug管理工具推荐：多款工具助力项目开发与管理

国际通用的bug管理工具有&#xff1a;1、Zoho Projects&#xff1b;2、Tracup&#xff1b;3、Bugtags&#xff1b;4、QC(QualityCenter)&#xff1b;5、Bugzilla&#xff1b;6、EasyBUG&#xff1b;7、Mantis&#xff1b;8、WebIssues。Zoho Projects拥有专业的缺陷管理模块&am…
阅读更多...
复数的三角形式与指数形式

复数的三角形式与指数形式

See https://blog.csdn.net/u011089570/article/details/102685877
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023