题目一
试题编号: 202112-1
试题名称: 序列查询
时间限制: 300ms
内存限制: 512.0MB

样例1输入
3 10
2 5 8
样例1输出
15
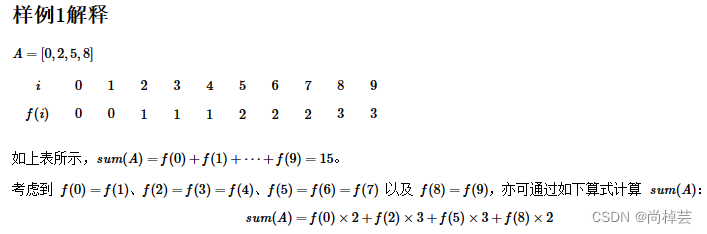
样例2输入
9 10
1 2 3 4 5 6 7 8 9
样例2输出
45

题目分析(个人理解)
- 还是先看输入,第一行输入n表示第二行有n个数,N表示有多大的范围,N表示序列i 范围[0,n),关键在于找到第二行内容输入的和f(i)之间的关系。i相当于位序,N确定了位序到哪结束,第二行表示在哪个位序开始赋值(值从1开始),第二行第二个以及之后的数值表示在此位序在前1位序值的基础上加一。
- 突然之间发现了一个巧妙的算法,其实题目中的提示也给出了,用乘法代替相同的数相加,比如以第一个样例为例子,我现在题目给的A列表中追加写入N,也就是A=[0,2,5,8,10]
- 那我最后输出的和就是从0遍历到n + 1
s += i * (A[i+1] - A[i]),
运算过程:13+23+3*2=15 - 最后输出s即可。
- 上代码!!!
n_N =list(map(int,input().split()))
#等价于 n_N = [int(num) for num in input().split()]
A = [0] + [int(a) for a in input().split()] + [n_N[1]]
S = 0
for i in range(n_N[0] + 1):S += i * (A[i+1] - A[i])
print(S)题目二
试题编号: 202112-2
试题名称: 序列查询新解
时间限制: 1.0s
内存限制: 512.0MB

样例1输入
3 10
2 5 8
样例1输出
5
样例2输入
9 10
1 2 3 4 5 6 7 8 9
Data
样例2输出
0
Data
样例3输入
2 10
1 3
Data
样例3输出
6

题目分析(个人理解)
- 我们可以看到测试的规模,如果利用暴力法,我们只能过70%样例,最后获得70%的分,所以不能直接用暴力的方法。暴力求解思路:先创建两个列表分别表示f(i)和g(i)最后依次遍历求作差之后的绝对值即可。
- 暴力求解的代码:理论上应该是le9+5但是会超时,显示0分。(le是科学计数法表示方法)
n, N = map(int, input().split())
ori_li = list(map(int, input().split()))f = [0 for _ in range(int(1e7 + 5))]
dif = [0 for _ in range(int(1e7 + 5))]
for i in ori_li:dif[i] = dif[i] + 1sum_f = 0
index = 1
fx = 0
r = (N // (n + 1))
for i in range(1, N):f[i] = f[i - 1] + dif[i]sum_f += abs(f[i] - (i // r))print(sum_f)-
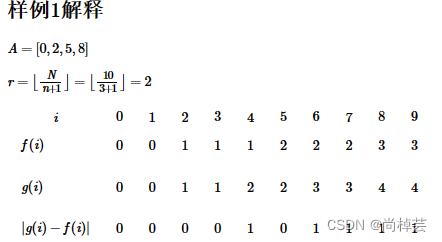
考虑用N太浪费时间,发现如果用n进行循环,时间就不会超出限制,又能够发现A[i-1]~A[i]内f的值都是一样的,所有的g的值其实就是i/r的整数部分,因此一开始想到把全部的f的值加起来,g的值加起来作差就行,但最后发现不对,因为中间有些做完差后需要取绝对值。
-
可以采用离散化加二分法,(学过概率论的同学指定知道离散型和连续型数据) 就考虑在已经分好的 A[i-1]~A[i]区间内再去找哪一部分大于g(这里由前面推论可知g的值和i有关,因此分别求出左右两端的区间端点g值判断划分即可),然后再以r为区间长度进行循环求解。
-
如何用二分查找算法:
-
bisect模块是Python标准库中的一个模块,提供了对有序列表的插入和搜索操作的支持。它基于二分查找算法,可以高效地在有序列表中查找或插入元素。
bisect模块中包含了以下主要函数和方法:
bisect(list, value, lo=0, hi=len(list), key=None):在有序列表中查找将值插入的位置,并返回该位置的索引,它是 bisect_right 的别名。
bisect_left(list, value, lo=0, hi=len(list), key=None):在有序列表中查找将值插入的位置,并返回左侧的索引(相同值的最左边位置)。
bisect_right(list, value, lo=0, hi=len(list), key=None):在有序列表中查找将值插入的位置,并返回右侧的索引(相同值的最右边位置)。
insort(list, value, lo=0, hi=len(list), key=None):将值插入有序列表中的适当位置,它是 insort_right 的别名。
insort_left(list, value, lo=0, hi=len(list), key=None):将值插入有序列表中的最左侧位置。
insort_right(list, value, lo=0, hi=len(list), key=None):将值插入有序列表中的最右侧位置。
这些函数和方法可用于处理各种有序列表的操作,如插入元素、查找元素的位置、维持列表的有序性等。 -
bisect
函数定义:bisect(list, value, lo=0, hi=len(list))
参数:
list: 有序列表。
value: 要插入的值。
lo (可选): 搜索的起始位置,默认为0。
hi (可选): 搜索的结束位置,默认为列表长度。
作用:在有序列表中查找将值插入的位置,并返回该位置的索引。 -
bisect_left
函数定义:bisect_left(list, value, lo=0, hi=len(list))
参数:与 bisect()函数相同。
作用:在有序列表中查找将值插入的位置,并返回左侧的索引(相同值的最左边位置)。
用法示例:
import bisect
numbers = [1, 3, 5, 5, 7, 9]#查找将值 5 插入 numbers 的最左侧索引位置
index = bisect.bisect_left(numbers, 5)
print(index) # 输出: 2
在这个例子中,列表 numbers中有两个值为5的元素。通过使用 bisect_left()函数,我们可以找到将值5插入到列表中的最左侧索引位置,即索引2。 -
其实这个解题思路还可以联想成一个频率分布直方图(实际频率分布直方图就是把连续型转化成离散型)。
-
上代码!!!
# 输入的数据
n,N = map(int,input().split())
A = [0]
A.extend(list(map(int,input().split())))
A.append(N)
r = N // (n+1)
B = []
for i in range(N//r + 2):if i*r >= N: break B.append(i*r)
B.append(N)
s = list(set(A+B))
s.sort()
L = len(s)
# 离散化
tree = [0]*(L-1)
from bisect import bisect_left as bl
for i in range(len(A) - 1):a,b = bl(s,A[i]),bl(s,A[i+1])for j in range(a,b):tree[j] += ifor i in range(len(B) - 1):a,b = bl(s,B[i]),bl(s,B[i+1])for j in range(a,b):tree[j] -= i
# tree求两边的差值的划分
ans = 0
for i in range(L-1):# tree[i]代表的是差值,s[i+1] - s[i]代表的是区间的长度ans += abs(tree[i]*(s[i+1]-s[i]))
print(ans)
- 第二种方法:
- 刚开始我只注意到在f(x)区间上分段,计算给定i(索引)下前g(x)的和,然后f(x)段和减去下面g(x)的和就可以了;事实上是我想太少了。因为在同样f(x)段下依然不能简单的减去g(x)的分段和;比如
f(x) 1 1 1
g(x) 0 1 2
|g(x)-f(x)| 1 0 1
如果按之前的思路,则计算结果为0,但实际结果为2;
这里里面涉及到的就是如果在同一段f(x)下,如果g(x)都小于f(x)或都大于f(x)的话可以直接相减,但如果有“转折点”的话就要再分情况计算了。 - 我们可以发现g(i)其实可以看作是r(N//(n+1))个首项为0,公差为1的等差数列;等差数列求和公式Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2,(r个完整的等差数列求和再加最后几个不完整的)。
- 判断是不是转折点:这里要判断要么区间内值全小于等于f(i),要么区间内值全大于等于f(i),这里f(i)实际就是i-1;这里等于放不放没影响,递增函数,同时满足这两个条件,有点像做高中数学函数恒成立问题。
- 如果没有转折点,直接f(x)区间和减g(x)区间和;如果有转折点,找出转折点,从转折点处分段求。
- 上代码!!!
n, N = tuple(map(int, input().split()))
# 有用的点
A = [0] + [int(x) for x in input().split()]# 计算gi数列下标到x的和
def h(x):if x <= 0:return 0global rx = x + 1n = x // rm = x % rreturn int(n * (r * (n - 1) / 2 + m))# 对下标为left到right的abs(fi-gi)求和,包括left和right两点
def cal(fi, left, right):return abs(h(right) - h(left - 1) - fi * (right - left + 1))# 判断是否有转折点,并返回error增加量
def ischange(fi, left, right):# 没有转折点if left // r >= fi or right // r <= fi:return cal(fi, left, right);# 出现转折点else:# 算出第一个转折点splitindex = left + r * (fi - (left + 1) // r) + r - (left + 1) % rreturn cal(fi, left, splitindex) + ischange(fi, splitindex + 1, right)r = N // (n + 1)
error = 0# 根据fi的数值来分组,开始遍历
for fi in range(n + 1):left = A[fi]if fi < n:right = A[fi + 1] - 1else:right = N - 1error += ischange(fi, left, right)print(error)总结
人生总有一段寂寞,孤独,淋着雨的路要自己走下去,如果你感到困难重重,那么说明你在爬上坡,你在进步;坚持下去,等你攀过高峰,淋过风雨,到达顶峰时就会知道坚持的意义了。 ——————————shangzhaoyun 2023.10.12