深度学习的概念源于人工神经网络的研究,神经网络是由多个神经元组成,。一个神经元由以下几个关键知识点组成:
①激活函数 ②损失函数 ③梯度下降
单个神经元的网络模型如图所示

用计算公式表达如下:
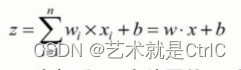
z为输出的结果,x为输入,w为权重,b为偏置值。z的计算过程是将输入的x与其对应的w相乘,然后再把结果加上偏置值b。
模型每次的训练学习是为了调整w和b从而得到一个合适的值,最终由这个值配合运算公式所形成的逻辑就是神经网络的模型。可以看一下大脑细胞里的神经突触。它和我们建立的模型有点神似。
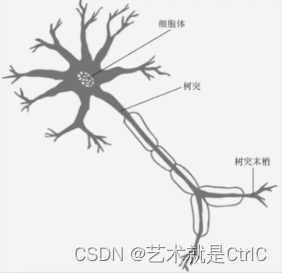
大脑神经细胞是靠生物电来传递信号的,可以把它理解成经过模型的具体数值
神经细胞相连的树突有粗有细,显然对通过不同粗细连接的生物电信号,会有不同的影响。这类似权重w,因为每个输入节点都会与相关连接的w相乘,也就实现了对信号的放大、缩小处理
中间的细胞体是不知道如何运作的。可以将所有输入的信号经过w变换之后,再添加一个额外的偏置量b,把它们加在一起求和,然后再选择一个模拟细胞体处理的函数(即激活函数)来实现整个过程的仿真。当通过调整w和b得到一个合适的值后,再配合合适的激活函数,就会发现它可以产生很好的拟合效果,从而得出细胞体的运作逻辑。
正向传播
模拟细胞体的仿真过程中,将数据从输入到输出的这种流向传递过程,称为正向传播。且该过程是在一个假设有合适的w和b的基础上,才可以实现对现实环境的正确拟合。然而,在现实环境中,是不知道w和b的值具体是多少才算正常的。
反向传播
反向传播的目的 : 告诉模型w和b的值调整到多少合适。
在一开始没有得到合适的权重时,正向传播生成的结果与实际的标签是有误差的,反向传播就是要把这个误差传递给权重,让权重做适当地调整来达到一个合适的输出。
代码示例如下:
#反向优化
cost = tf.reduce_mean(tf.square(Y - z))
learning_rate = 0.01
#使用梯度下降算法
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)实际训练过程中,模型需要通过多次迭代一点一点的修正,直到输出值与实际标签值的误差小于某个阈值为止。这个过程中,还需要将输出的误差转化为权重的误差,经常使用的算法是误差反向传播算法,也就是BP算法。
为了要让损失值变得最小化,需要通过对其求导的方式,找到最小值时刻的函数切线斜率(也就是梯度),从而让w和b的值沿着这个梯度来调整。至于每次调整多少,我们引入一个叫做"学习率"的参数来控制,这样通过不断的迭代,使误差逐步接近最小值,最终找到w和b的合适值,达到拟合的效果。
误差反向传播算法-BP算法的思想
反向传播使用的BP算法是应用较为广泛的一种参数学习算法。它是一种按照误差逆向传播算法训练的多层前馈神经网络。
该算法的核心思想就是通过输出层得到输出结果和期望输出的误差来间接调整隐层的权值。
BP算法的模型示意图如下:
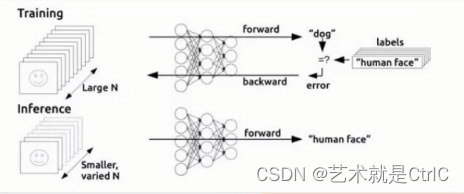
BP算法的学习过程由信号的正向传播(求损失)与误差的反向传播(误差回传)两个过程组成:
正向传播FP(求损失) : 在这个过程中,根据输入的样本、给定的初始化权重值w和偏置量b,计算最终输出值以及输出值与实际值之间的损失值。如果损失值不在给定的范围内则进行反向传播的过程,否则停止w、b的更新。
反向传播BP(回传误差) : 将输出以某种形式通过隐层向输入层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。
由于BP算法是通过传递误差值δ进行更新求解权重值w和偏置值b,所以BP算法也常常被叫做δ算法。
![[Python]黑色背景白色块滑动视频](https://img-blog.csdnimg.cn/b604defed3734368849960d962c145a3.png)