汉诺塔问题

本文部分截图来源：汉诺塔可视化小游戏
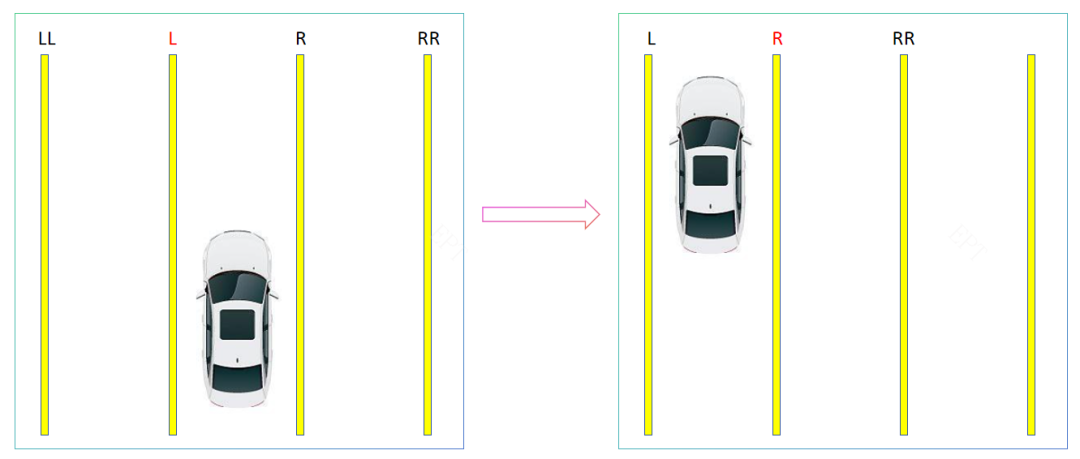
移动最终目标：将A柱中的所有盘移动至C柱
移动过程要求：1.每次只能移动一个盘 2.每次移动后必须保证小盘在大盘上方

问题简化
我们先将三个盘（n-1，n=4）看作一个整体，这样问题简化为2个盘的移动，接下来我们按照这个简化版本试着移动一下
将A柱上n-1个盘借助C转移到B

Hanoi(n-1,a,c,b);//n-1个盘从A借助C移到B

将A柱上剩下的一个转移到C

Move(n,a,c);//将n个盘从A移到C

将n-1个盘从B柱借助A转移到C

Hanoi(n-1,b,a,c);//n-1个盘从B借助A移到C

前n-1看作整体完成移动、前n-2看作整体完成移动 $\cdots$ 1个完成移动

总体操作：
（1）将n-1个盘从一个柱借助辅助柱转移到另一个柱（n>1，递归过程）
（2）将剩余一个盘从一个柱转移到另一个柱（n==1，递归出口）

完整代码：

#include<stdio.h>
#include<windows.h>
void Hanoi(int n,char a,char b,char c);
void Move(int n,char a,char b);
int count;
int main(){int n=0;printf("Hanoi 层数:");scanf("%d",&n);Hanoi(n,'A','B','C');Sleep(20000);return 0;
}
void Hanoi(int n,char a,char b,char c){if (n==1){Move(n,a,c);//最后一个盘从A移到C}else{Hanoi(n-1,a,c,b);//n-1个盘从A借助C移到BMove(n,a,c);//将n个盘从A移到CHanoi(n-1,b,a,c);//n-1个盘从B借助A移到C}
}
void Move(int n,char a,char b){count++;printf("第%d次移动Move%d:Move from %c to %c\n",count,n,a,b);
}