Git 分布式版本控制工具使用教程

1.关于Git

1.1 什么是Git

Git是一款免费、开源的分布式版本控制工具，由Linux创始人Linus Torvalds于2005年开发。它被设计用来处理从很小到非常大的项目，速度和效率都非常高。Git允许多个开发者几乎同时处理同一个项目而不会互相干扰，并且在合并各自的修改时提供强大的支持。主要用于管理开发过程中的源代码文件（Java类、xml文件、html页面等）。
其他的版本控制工具：SVN、CVS、VSS

1.2 Git的作用

代码回溯：Git在管理文件过程中会记录日志，方便回退到历史版本

        Git在每次提交时都会创建一个唯一的提交ID，并记录下文件的快照。这意味着您可以随时查看项目的历史版本，了解每个文件的变化历程，甚至可以恢复到任意一个历史状态。

应用场景：

        错误修复：如果新添加的代码导致了bug，可以通过git log找到引入问题的提交，然后使用git revert或git reset撤销该次提交。

        实验性开发：在尝试新的特性或修改现有代码结构时，如果发现改动不理想，可以轻松回退到稳定版本。

版本切换：Git存在分支的概念，一个项目可以有多个分支（版本），可以任意切换

        分支允许开发者在不影响主线（通常是main或master分支）的情况下进行新功能的开发、测试或修复bug。通过切换分支，可以在不同的开发任务之间快速切换

应用场景：

        并行开发：团队成员可以在各自的分支上工作，互不干扰。例如，前端开发人员可以在feature/frontend分支上工作，而后端开发人员则在feature/backend分支上工作。
        紧急修复：当需要对线上版本进行紧急修复时，可以从生产分支（如release分支）创建一个修补分支（hotfix），修复完成后合并回生产分支。

多人协作：Git支持多人协作，即一个团队共同开发一个项目，每个团队成员负责一部分代码，通过Git就可以管理和协调

        Git通过分布式版本控制系统使得团队协作更加高效。每个人都可以拥有完整的项目副本，包括历史记录，这样即使没有网络连接也能继续工作。

应用场景：

        代码审查：提交代码前，通常会发起一个Pull/Merge Request，邀请其他团队成员审查代码。这有助于提高代码质量，确保最佳实践得到遵循。

        冲突解决：当多个开发者同时修改同一部分代码时，可能会发生冲突。Git提供了工具帮助识别和解决这些冲突。

远程备份：Git通过仓库管理文件，在Git中存在远程仓库，如果本地文件丢失还可以从远程仓库获取

        远程仓库不仅用于同步团队成员的工作进度，也是一个重要的备份手段。即便本地环境出现问题，也可以从远程仓库恢复丢失的数据。

应用场景：

        灾难恢复：如果本地电脑损坏或者误删了重要文件，可以从远程仓库重新克隆整个项目。
        跨设备同步：开发者可以在不同设备上工作，只需通过git pull和git push命令保持各处代码库的一致性。

2.Git概述

2.1 Git简介

Git 仓库分为两种：
本地仓库：开发人员自己电脑上的 Git 仓库
远程仓库：远程服务器上的 Git 仓库

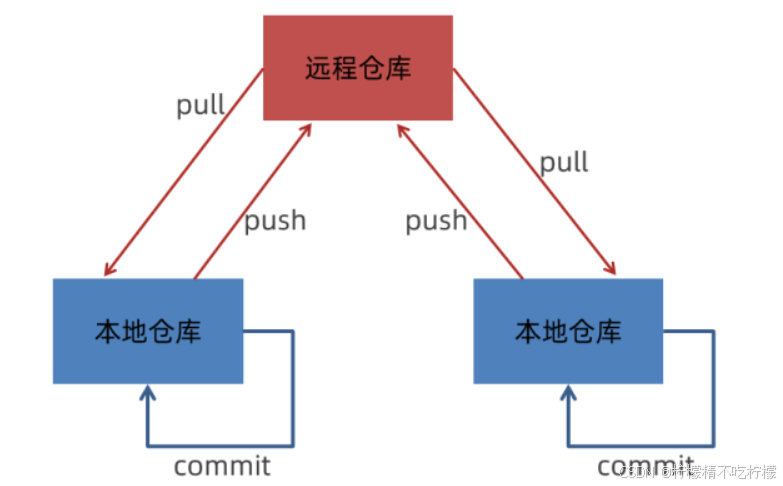
commit：提交,将本地文件和版本信息保存到本地仓库
push：推送,将本地仓库文件和版本信息上传到远程仓库
pull：拉取,将远程仓库文件和版本信息下载到本地仓库

2.2 Git下载与安装

官方下载地址： https://git-scm.com/download
选择合适的版本，下载完成后，双击完成安装即可，安装完成后可以在任意目录下点击鼠标右键，如果能够看到如下菜单则说明安装成功

Git GUI Here：打开Git 图形界面

Git Bash Here：打开Git 命令行

Git安装目录结构如下

3. Git 和代码托管中心

代码托管中心是基于网络服务器的远程代码仓库，通常简称为远程库。它允许开发者存储、管理和共享他们的代码，并支持团队协作开发。根据其部署和访问方式的不同，可以分为局域网内的私有部署和互联网上的公共或私有服务。

局域网
在企业内部或者特定组织内，为了更好地控制数据安全和访问权限，可以选择在局域网内搭建自己的远程代码仓库。

GitLab：一个开源的分布式版本控制系统，允许用户自行搭建并管理自己的远程代码仓库。GitLab提供了丰富的功能，包括项目管理、持续集成/持续部署（CI/CD）等，适用于各种规模的企业。
Gogs：Gogs是一款极易搭建的自助Git服务，具有轻量级、易于安装的特点。适合希望快速部署一个简单但功能齐全的Git服务器的小型团队或个人开发者。

互联网
对于需要跨地域协作的团队或希望公开分享自己项目的个人开发者，互联网上的代码托管平台是更好的选择。

GitHub：全球最大的代码托管平台之一，拥有庞大的开源社区。尽管它是外网服务，在某些地区可能无法直接访问，但它依然是全球开发者进行代码分享与合作的重要场所。
Gitee (码云)：作为国内知名的代码托管平台，Gitee为中国的开发者提供了一个高效、稳定的环境来托管代码。它支持公有和私有仓库，非常适合中国境内的团队和个人使用，特别是在需要遵守国内法律法规的情况下。

无论是选择局域网内的私有部署方案还是互联网上的公共平台，合适的代码托管中心都能极大提升团队的开发效率，促进知识共享和技术进步。同时，考虑到不同地区的网络环境和法律要求，选择适合自己需求的服务至关重要。

4. Git常用命令

4.1 Git全局设置

在安装Git后，首先要进行的步骤是配置用户名称和电子邮件地址。这是因为每次提交更改时，Git都会使用这些信息来标识提交者。

设置用户信息

执行以下命令来设置全局用户名和电子邮件地址

git config --global user.name "你的名字"
git config --global user.email "你的邮箱地址"//例如
git config --global user.name "张三"
git config --global user.email "zhangsan@example.com"

查看配置信息

通过以下命令查看当前的所有Git配置项

git config --list

其他配置：

设置文本编辑器
默认情况下，Git会使用系统的默认文本编辑器（如vim或nano）。如果你有偏好使用的编辑器，可以通过以下命令设置

git config --global core.editor "编辑器路径"//例如使用VS Code编辑器
git config --global core.editor "code --wait"

配置别名

为了简化常用的Git命令，可以为它们创建别名

git config --global alias.co checkout
git config --global alias.br branch
git config --global alias.ci commit
git config --global alias.st status//也可以使用简短的命令执行
git co   # 等同于 git checkout
git br   # 等同于 git branch
git ci   # 等同于 git commit
git st   # 等同于 git status

查看特定配置项

如果想查看某个特定配置项的值，可以使用以下命令

git config [键名]//例如查看用户名
git config user.name

4.2 获取Git仓库

要使用Git对代码进行管理，首先需要获得一个Git仓库。获取Git仓库通常有两种方式：在本地初始化一个新的Git仓库或从远程仓库克隆。

4.2.1 在本地初始化Git仓库

假设有一个新的项目，还没有任何版本控制，可以在本地初始化一个新的Git仓库。

1.创建一个空目录

在任意位置创建一个新的空目录，作为你的本地Git仓库。例如，在命令行中执行

mkdir repo1//创建目录
cd repo1//进入目录

2.打开Git Bash窗口

选择“Git Bash Here”来打开Git Bash窗口。

3.初始化Git仓库

在Git Bash窗口中执行以下命令来初始化一个新的Git仓库，这将创建一个名为.git的隐藏文件夹，包含Git所需的所有元数据和配置文件

git init

4.验证Git仓库是否成功创建

使用以下命令查看当前目录下的所有文件（包括隐藏文件），如果看到.git文件夹，则说明Git仓库已经成功创建

ls -a

5.添加初始文件并提交

接下来可以添加一些初始文件，并进行第一次提交

echo "# My New Project" >> README.md
git add README.md
git commit -m "Initial commit"

4.2.2 从远程仓库克隆

从远程仓库克隆是更常见的方式，特别是需要参与一个已有的项目或者基于某个开源项目进行开发时。

1.找到远程仓库地址

首先你需要知道远程仓库的URL。这通常是一个HTTPS或SSH地址，例如：

GitHub: https://github.com/username/repository.git
GitLab: git@gitlab.com:username/repository.git
Gitee: https://gitee.com/username/repository.git

2.执行克隆命令

HTTPS vs SSH：克隆仓库时可以选择使用HTTPS或SSH协议。HTTPS不需要额外配置，但每次操作都需要输入用户名和密码（或个人访问令牌）。SSH则需要配置公钥/私钥对，但一旦配置完成，后续操作无需重复输入凭证

git clone https://github.com/username/repository.git//或者使用SSH方式
git clone git@github.com:username/repository.git

除了git clone外，还有其他常用的远程仓库管理命令，如git remote add（添加新的远程仓库）、git remote remove（移除远程仓库）等

3.进入克隆下来的仓库目录

克隆完成后，会自动创建一个与远程仓库同名的目录。进入该目录

cd repository

4.查看当前状态

可以使用以下命令查看当前仓库的状态，确认所有文件都已正确下载

git status

5.拉取最新更新

如果远程仓库有其他人提交了新的更改，可以使用以下命令拉取最新的更新

//这里的main是默认的主分支名称，具体分支名称可能有所不同
git pull origin main

克隆下来的仓库默认会切换到远程仓库的默认分支（通常是main或master）。可以通过

git branch命令查看所有分支，并使用git checkout或git switch切换分支

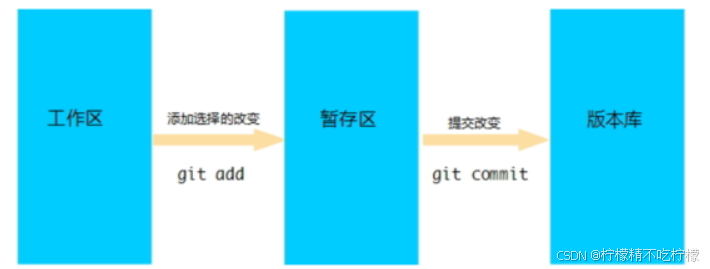
4.3 工作区、暂存区、版本库

4.3.1 版本库

版本库是指包含.git隐藏文件夹的整个目录结构，它是Git用来管理项目历史记录的核心组件。版本库存储了项目的完整历史记录、配置信息、日志信息以及各个文件的不同版本

位置： .git文件夹通常位于你的工作区根目录下，并且默认是隐藏的。
内容： 版本库包含了所有提交的历史记录、分支信息、标签、配置文件等。它还保存了每次提交的快照，而不是简单的差异（diff）。
用途： 版本库可以轻松地查看项目的历史版本，回滚到任意一个历史状态，或者在不同的分支之间切换。
ls -a
# 输出可能包括 .git 文件夹

4.3.2 工作区

工作区是指包含.git文件夹的目录，也就是你当前正在工作的目录。在这个目录中，你可以直接编辑文件、添加新文件或删除文件

位置：工作区是你日常开发的主要场所，通常是你打开代码编辑器的地方。
内容：包含所有的源代码文件、资源文件和其他相关文档。这些文件可以是未被Git跟踪的新文件，也可以是已经提交过的旧文件。
用途：工作区是编写和测试代码的地方。在这里，你可以自由地修改文件，然后决定哪些更改需要提交到版本库。

4.3.3 暂存区

暂存区是一个临时区域，用于存放即将提交到版本库的更改。它位于.git文件夹内的index文件中。暂存区允许你在提交之前选择哪些更改应该包含在下一个提交中

位置： 暂存区实际上是由.git/index文件表示的，但它通常被称为“暂存区”或“stage”。
内容： 暂存区保存了那些已经被标记为将要提交的文件更改。这些更改在暂存区中等待最终提交到版本库。
用途： 暂存区提供了一个中间步骤，让你可以在提交之前仔细检查和选择要包含的更改。这有助于保持提交的清晰和有组织性。
//添加文件到暂存区
git add filename.txt//查看暂存区状态
git status//从暂存区移除文件
git reset filename.txt//提交（commit）
git commit -m "本次提交的描述信息"//推送本地提交到远程仓库
git push

4.4 Git工作区中文件的状态

Git工作区中的文件存在两种状态：

untracked 未跟踪（未被纳入版本控制）
tracked 已跟踪（被纳入版本控制）

        1）Unmodified 未修改状态
        2）Modified 已修改状态
        3）Staged 已暂存状态
注意：文件的状态会随着我们执行Git的命令发生变化

4.5 本地仓库操作

本地仓库常用命令如下：

git status 查看文件状态，由于工作区中文件状态的不同，执行 git status 命令后的输出也会不同
git add 将文件的修改加入暂存区，命令格式：git add fileName。加入暂存区后再执行 git status 命令，可以发现文件的状态已经发生变化
git reset 将暂存区的文件取消暂存或者是切换到指定版本（注意：每次Git提交都会产生新的版本号，通过版本号就可以回到历史版本）

取消暂存命令格式：git reset 文件名

切换到指定版本命令格式：git reset --hard 版本号

git commit 将暂存区的文件修改提交到版本库，命令格式：git commit -m msg 文件名

-m：代表message，每次提交时需要设置，会记录到日志中
可以使用通配符*一次提交多个文件

git log 查看日志，通过git log命令查看日志，可以发现每次提交都会产生一个版本号，提交时设置的message、提交人、邮箱、提交时间等信息都会记录到日志中

4.6 远程仓库操作

远程仓库常用命令如下：

git remote 查看远程仓库，如果要查看已经配置的远程仓库服务器，可以执行 git remote 命令，它会列出每一个远程服务器的简称。
如果已经克隆了远程仓库，那么至少应该能看到 origin ，这是 Git 克隆的仓库服务器的默认名字。

可以通过-v参数查看远程仓库更加详细的信息
本地仓库配置的远程仓库都需要一个简称，后续在和远程仓库交互时会使用到这个简称

git remote add 添加远程仓库，添加远程仓库命令格式：git remote add 简称远程仓库地址

一个本地仓库可以关联多个远程仓库

git clone 从远程仓库克隆，Git 克隆的是该Git 仓库服务器上的几乎所有数据（包括日志信息、历史记录等）。克隆仓库的命令格式： git clone 远程仓库地址
git pull 从远程仓库获取最新版本并合并到本地仓库，命令格式：git pull 远程仓库简称分支名称

如果当前本地仓库不是从远程仓库克隆，而是本地创建的仓库，并且仓库中存在文件，此时再从远程仓库拉取文件的时候会报错（fatal: refusing to merge unrelated histories ）
解决此问题可以在git pull命令后加入参数--allow-unrelated-histories

git push 推送到远程仓库，将本地仓库内容推送到远程仓库，
命令格式：git push 远程仓库简称
分支名称在使用git push命令将本地文件推送至远程仓库时，如果是第一次操作，需要进行身份认证，认证通过才可以推送，如下

上面的用户名和密码对应的就是我们用户名和密码，认证通过后会将用户名和密码保存到
windows系统中，后续再推送则无需重复输入用户名和密码。