1、背景简介
xgboost+lr模型融合方法用于分类或者回归的思想最早由facebook在广告ctr预测中提出,其论文Practical Lessons from Predicting Clicks on Ads at Facebook有对其进行阐述。在这篇论文中他们提出了一种将xgboost作为feature transform的方法。大概的思想可以描述为如下:先用已有特征训练XGBoost模型,然后利用XGBoost模型学习到的树来构造新特征,最后把这些新特征加入原有特征一起训练模型。构造的新特征向量是取值0/1的,向量的每个元素对应于XGBoost模型中树的叶子结点。当一个样本点通过某棵树最终落在这棵树的一个叶子结点上,那么在新特征向量中这个叶子结点对应的元素值为1,而这棵树的其他叶子结点对应的元素值为0。新特征向量的长度等于XGBoost模型里所有树包含的叶子结点数之和。最后将新的特征扔到LR模型进行训练。实验结果表明xgboost+lr能取得比单独使用两个模型都好的效果。
2、原理介绍
“特征决定了所有算法效果的上限,而不同的算法只是离这个上限的距离不同而已。”所以如何更有效的提取有效的特征是机器学习中的一个hotspot,例如近几年来大火的深度学习方法中神经网络的层数不断增加其实质也是在探索如何更好地从原始数据中得到更为有效的特征表达。如果能够将数据表达成为线性可分的数据,那么使用简单的线性模型就可以取得很好的效果。
XGBoost 构建新的特征也是使特征更好地表达数据。它的核心思想是将boosting看作是一个将样本进行非线性变换的方法。处理特征变换的一般方法有:
- 对于连续的特征:一个简单的非线性变化就是将特征划分到不同的区域(bin),然后再将这些区域的编号看作一个离散的特征来进行训练。这也就是俗称的连续变量离散化方法,这有非常多的方法可以完成这项事情。
- 对于离散的特征:我们可以直接对离散特征做一个笛卡尔积从而得到一系列特征的组合,当然有些组合是没用的,那些没用的组合可以删掉。
- 而这里利用boosting来对样本进行离散化的方法是另一种特征变换的方法。
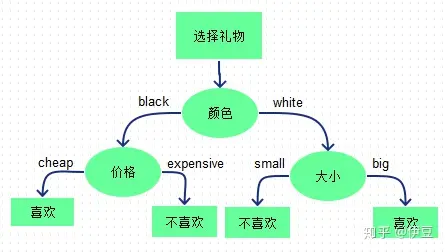
下面的图中的两棵树是利用现有特征训练XGBoost学习到的,其中第一棵树有3个叶子结点,而第二棵树有2个叶子节点。对于一个输入样本点x,如果它在第一棵树最后落在其中的第二个叶子结点,而在第二棵树里最后落在其中的第一个叶子结点。那么通过XGBoost获得的新特征向量为[0, 1, 0, 1, 0],其中向量中的前三位对应第一棵树的3个叶子结点,后两位对应第二棵树的2个叶子结点。下图为混合模型结构。输入特征通过增强的决策树进行转换。 每个单独树的输出被视为稀疏线性分类器的分类输入特征。 增强的决策树被证明是非常强大的特征转换。
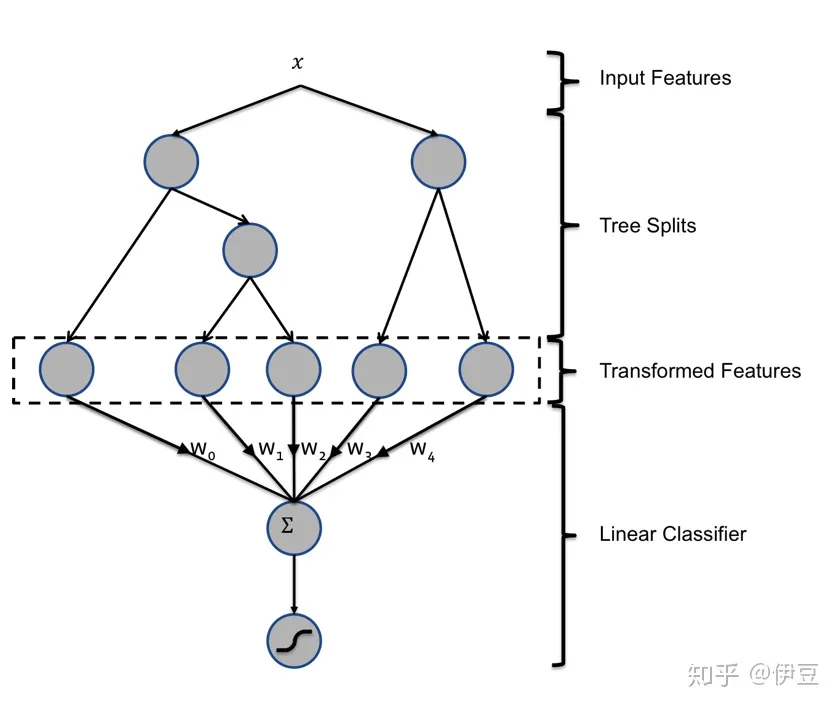
这里我们可以这样理解,XGBoost是一种集成树模型,其本质是不同单个决策树的组合。而决策树是一种树形结构,又称为判定树,是运用于分类的一种树结构,其中的每个内部节点代表对某一属性的一次测试,每条边代表一个测试结果,叶节点代表某个类或类的分布。决策树的决策过程需要从决策树的根节点开始,待测数据与决策树中的特征节点进行比较,并按照比较结果选择选择下一比较分支,直到叶子节点作为最终的决策结果。