【算法学习】-【滑动窗口】-【长度最小的子数组】

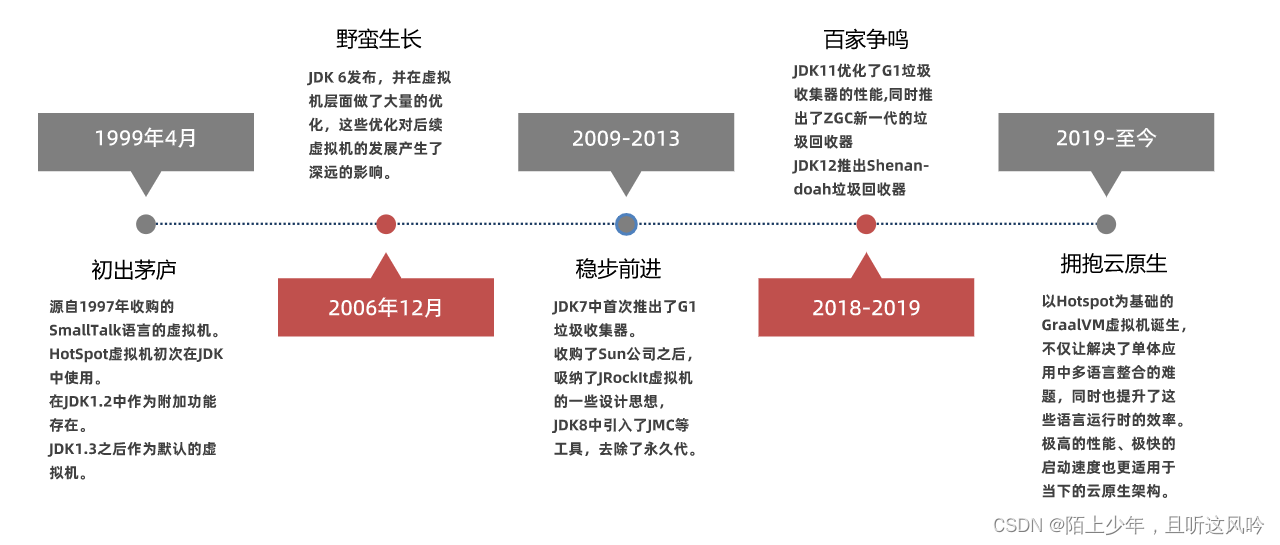
LeetCode原题链接：209. 长度最小的子数组

下面是题目描述：
给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

1 <= target <= 10⁹
1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁵

1、解题思路
相比双指针，滑动窗口算法更体现了对暴力枚举的优化，下面先简单介绍一下暴力枚举的思路，接着着重介绍优化思路及可以优化的原因，也就是滑动窗口算法。

（1）暴力枚举
题目要求找出该数组中满足其总和大于等于 target 的长度最小的连续子数组，那么就可以从第一个元素开始枚举，直至满足题目要求后记录一下长度；然后接着从第二个元素再枚举，直至枚举完所有情况。
如示例1：
第一次枚举：[2,3,1,2]，从2开始计算总和，最后总和为8，长度为4；
第二次枚举：[3,1,2,4]，从3开始计算总和，最后总和为10，长度为4；
第三次枚举：[1,2,4]，从1开始计算总和，最后总和为7，长度为3；
第四次枚举：[2,4,3]，从2开始计算总和，最后总和为9，长度为3；
第五次枚举：[4,3]，从4开始计算总和，最后总和为7，长度为2；
故最后结果为2。
（2）滑动窗口
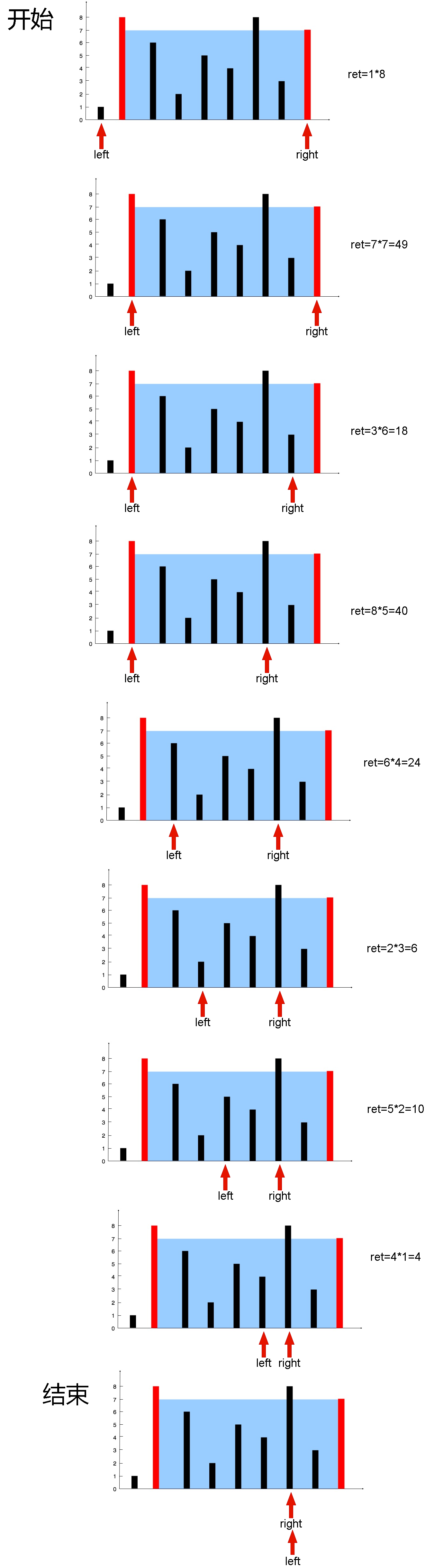
那么从上面暴力枚举的过程来看，其实有很多工作是重复的。如在第二次枚举中，就没必要再从3开始重新计算总和，因为此时相比于第一次枚举而言，计算的总和仅减去了一个2而增加了一个4。示意图如下所示：
在这里插入图片描述

那么可以看到，从红框到蓝框，就好像一个窗口在“滑动”。由于其避免了一些重复工作，有些时候也被称为是一种“备忘录”算法。

对于具体的实现，其实是两个同向指针来维护和更新这个“窗口”的，那么下面根据上面的优化思想，介绍一下滑动窗口算法的步骤：

第一步，进窗口
根据不同题目有不同的进窗口条件，本题的条件为：总和大于等于target；
这里创建两个指针begin和cur，初始都指向第一个元素；接着需要一个变量sum来判断当前总和是否满足条件；若不满足，则进窗口，即让sum加上当前元素：sum+=nums[begin]；若满足，则进行下一步。
第二步，循环出窗口和更新结果
所谓出窗口其实就是准备进行下一次遍历枚举（或者说“创造”下一次枚举的条件）
根据不同的题目有不同的更新结果的时机，一般在进行出窗口前可进行结果的更新。对于本题而言，出窗口前，cur-begin为本次枚举所得的子数组的长度，将其与上一次枚举所得的结果进行对比，取较小者即可：len = len < cur - begin ? len : cur - begin；接着，通过循环出窗口，即让sum减掉begin指向的元素，然后让begin往后走：sum -= nums[begin++]，循环直到sum值不满足条件为止而准备进行下一次的枚举。
（PS：可以看出来，实现滑动窗口越也需要用到两层循环，上述过程将进窗口设置在外循环而出窗口设置在内循环。当然也可反过来实现，但个人觉得将进窗口设置在外循环更好控制，代码也更易读些）

2、具体代码

    int minSubArrayLen(int target, vector<int>& nums) {int len = INT_MAX;int sum = 0;int begin = 0;int cur = 0;while(cur < nums.size()){        //进窗口sum += nums[cur++];//出窗口和更新while(sum >= target){len = min(len, cur - begin); sum -= nums[begin++];                     }}       return len == INT_MAX ? 0 : len;               }