数据结构与算法（三）

9 链表及其相关面试题

• 内容：
  • 链表查找、面试题的常见技巧
  • 链表回文
  • 链表的分区
  • 链表的复制

9.1 链表查找

• 输入链表头节点，奇数长度返回中点，偶数长度返回上中点；
• 输入链表头节点，奇数长度返回中点，偶数长度返回下中点；
• 输入链表头节点，奇数长度返回中点前一个，偶数长度返回上中点前一个；
• 输入链表头节点，奇数长度返回中点前一个，偶数长度返回下中点前一个。

// 输入链表头节点，奇数长度返回中点，偶数长度返回上中点
public static Node midOrUpMidNode(Node head) {// 空节点、1个节点、2个节点，都是返回headif (head == null || head.next == null || head.next.next == null) return head;// 3个节点或以上，定义快、慢指针Node slow = head, fast = head;// 当快指针可以走两步时，慢指针每次走一步，快指针走两步while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}return slow;
}// 输入链表头节点，奇数长度返回中点，偶数长度返回下中点
public static Node midOrDownMidNode(Node head) {// 空节点、1个节点，都是返回headif (head == null || head.next == null) return head;// 2个节点或以上，定义快、慢指针Node slow = head, fast = head;// 当快指针可以走两步时，慢指针每次走一步，快指针走两步while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}// fast.next == null 说明是奇数个节点，否则是偶数个节点return fast.next == null ? slow : slow.next;
}// 输入链表头节点，奇数长度返回中点前一个，偶数长度返回上中点前一个
public static Node midOrUpMidPreNode(Node head) {// 空节点、1个节点、2个节点，都是返回nullif (head == null || head.next == null || head.next.next == null) return null;// 3个节点或以上，定义快、慢指针Node slow = head, fast = head;// fast先走2步fast = fast.next.next;// 当快指针还可以走两步时，慢指针每次走一步，快指针走两步while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}return slow;
}// 输入链表头节点，奇数长度返回中点前一个，偶数长度返回下中点前一个
public static Node midOrDownMidPreNode(Node head) {// 空节点、1个节点，都是返回nullif (head == null || head.next == null) return null;// 2个节点，返回headif (head.next.next == null) return head;// 3个节点或以上，定义快、慢指针Node slow = head, fast = head;// fast先走1步fast = fast.next;// 当快指针还可以走两步时，慢指针每次走一步，快指针走两步while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}return slow;
}

• 面试时链表解题的方法论
  • 对于笔试，不用太在乎空间复杂度，一切为了时间复杂度；
  • 对应面试，时间复杂度依然放在第一位，但一定要找到空间最省的方法。
• 常用数据结构和技巧
  • 使用容器（哈希表、数组等）
  • 快慢指针

9.2 给定一个单链表的头节点head，请判断该链表是否为回文结构

• 哈希表方法特别简单（笔试用）
• 改原链表的方法就需要注意边界了（面试用）
• 测试链接：https://leetcode.cn/problems/palindrome-linked-list-lcci/description/

方法一：借助容器 栈，额外空间O(N)

public static boolean isPalindromeByStack(Node head) {Stack<Node> stack = new Stack<>();Node cur = head;while (cur != null) {stack.push(cur);cur = cur.next;}cur = head;while (cur != null) {if (cur.val != stack.pop().val) return false;cur = cur.next;}return true;
}

方法二：还是利用栈，只将右半部分入栈，额外空间O(N/2)

public static boolean isPalindromeByHalfStack(Node head) {if (head == null || head.next == null) return true;// 找中点Node slow = head, fast = head;while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}// 中点之后的节点入栈Stack<Node> stack = new Stack<>();while (slow.next != null) {stack.push(slow.next);slow = slow.next;}Node cur = head;// 依次弹出栈中元素比较while (!stack.isEmpty()) {if (cur.val != stack.pop().val) return false;cur = cur.next;}return true;
}

方法三：翻转链表中点位置以后的链表，额外空间O(1)

public static boolean isPalindrome(Node head) {if (head == null || head.next == null) return true;// 1. 快慢指针找中点Node slow = head, fast = head;while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}// 2. 逆序中点(奇数节点时slow中点、偶数节点时slow是上中点)之后的链表Node revHead = null, cur = slow.next, next;slow.next = null;while (cur != null) {next = cur.next;cur.next = revHead;revHead = cur;cur = next;}// 3. 头尾比较，判断是否是回文Node p = revHead;cur = head;boolean ans = true;while (cur != null && p != null) {if (cur.val != p.val) {ans = false;break;}cur = cur.next;p = p.next;}// 4. 恢复原链表Node pre = null;cur = revHead;while (cur != null) {next = cur.next;cur.next = pre;pre = cur;cur = next;}slow.next = pre;return ans;
}

9.3 链表的分区

• 给定一个单链表的头节点head，给定一个整数n，将链表按n划分成左边<n、中间==n、右边>n
  • 把链表放入数组中，在数组上做partition（笔试用）
  • 分成小、中、大三部分，再把各个部分之间串起来（面试用）

方法一：借助数组分区

方法二：不借助容器public static Node listPartitionByArray(Node head, int pivot) {if (head == null) return null;// 1. 遍历链表，计算链表节点个数Node cur = head;int cnt = 0;while (cur != null) {cnt++;cur = cur.next;}// 2. 创建一个Node数组，再次遍历原链表，将每个节点加入数组中Node[] nodes = new Node[cnt];cur = head;for (int i = 0; i < cnt; i++) {nodes[i] = cur;cur = cur.next;}// 3. 分区int small = -1, big = cnt, idx = 0;while (idx < big) {if (nodes[idx].val == pivot) idx++;else if (nodes[idx].val < pivot) swap(nodes, ++small, idx++);else swap(nodes, --big, idx);}// 4. 将数组中的节点串联起来for (int i = 1; i < cnt; i++) nodes[i - 1].next = nodes[i];nodes[cnt - 1].next = null;return nodes[0];
}
private static void swap(Node[] nodes, int i, int j) {if (i == j) return;Node tmp = nodes[i];nodes[i] = nodes[j];nodes[j] = tmp;
}

方法二：不借助容器

public static Node listPartition(Node head, int pivot) {// 定义6个变量分别是 小于区、等于区、大于区 的头和尾指针，和Node sh = null, st = null, eh = null, et = null, bh = null, bt = null;// 定义一个cur用于遍历head链表，next用于记录下一步Node cur = head, next;// 遍历原链表进行分区while (cur != null) {next = cur.next;cur.next = null;if (cur.val < pivot) {if (sh == null) sh = cur;else st.next = cur;st = cur;} else if (cur.val == pivot) {if (eh == null) eh = cur;else et.next = cur;et = cur;} else {if (bh == null) bh = cur;else bt.next = cur;bt = cur;}cur = next;}// 用小于区域的尾巴，去连等于区域的头if (st != null) {// 如果有小于区域st.next = eh;// 下一步，谁去连大于区域的头，谁就变成eTet = et == null ? st : et;}// 用等于区域的尾巴，去连大于区域的头if (et != null) et.next = bh;return sh != null ? sh : (eh != null ? eh : bh);
}

9.4 链表的复制

• 一种特殊的单链表节点类描述如下：

class Node {int value;Node next;Node rand;Node(int val) {value = val;}
}

• rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点head，请实现一个函数完成这个链表的复制，返回复制的新链表的头节点，要求时间复杂度O(N)，额外空间复杂度O(1)。
• 测试链接 : https://leetcode.cn/problems/copy-list-with-random-pointer/

方法一：借助容器Map

public static Node copyRandomListByMap(Node head) {// key: 老节点，value: 新节点Map<Node, Node> nodeMap = new HashMap<>();// 1. 定义一个指针遍历原链表，将所有节点克隆一份，并和来节点建立映射关系Node cur = head;while (cur != null) {nodeMap.put(cur, new Node(cur.val));cur = cur.next;}// 2. 再次遍历原链表，设置新链表的next和randomcur = head;while (cur != null) {Node newNode = nodeMap.get(cur);newNode.next = nodeMap.get(cur.next);newNode.random = nodeMap.get(cur.random);cur = cur.next;}return nodeMap.get(head);
}

方法二：不借助容器

public static Node copyRandomList(Node head) {if (head == null) return null;// 定义一个指针遍历原链表，和next记录下一步// 1. 将所有节点克隆一份，挂在每个节点的后面// 1->2->3->null  ==>> 1->1'->2->2'->3->3'->nullNode cur = head, next;while (cur != null) {next = cur.next;cur.next = new Node(cur.val);cur.next.next = next;cur = next;}// 2. 依次设置 1' 2' 3' random指针cur = head;while (cur != null) {next = cur.next.next;Node copy = cur.next;copy.random = cur.random == null ? null : cur.random.next;cur = next;}// 3. 分拆新老节点cur = head;Node copyHead = head.next;while (cur != null) {next = cur.next.next;Node copy = cur.next;cur.next = next;copy.next = next == null ? null : next.next;cur = next;}return copyHead;
}

10 链表相关面试题（续）、二叉树的常见遍历

• 内容：
  • 单链表的相交节点系列问题
  • 一种看似高效其实搞笑的节点删除方式
  • 二叉树的中序、先序、后序遍历

10.1 判断链表相交

• 给定两个可能有环也可能无环的单链表，头节点head1和head2。请实现一个函数，如果两个链表相交，请返回相交的第一个节点。如果不相交返回null。要求如果两个链表长度之和为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

// 返回两个链表相交节点，不相交返回null
public static Node getIntersectNode(Node head1, Node head2) {if (head1 == null || head2 == null) return null;// 1. 分别获取两个链表的入环节点Node loop1 = getLoopNode(head1);Node loop2 = getLoopNode(head2);// 2. 情况一：两个链表都无环if (loop1 == null && loop2 == null) {return getIntersectWithNoLoop(head1, head2);}// 2. 情况二：两个链表都有环if (loop1 != null && loop2 != null) {return getIntersectWithBothLoop(head1, loop1, head2, loop2);}// 3. 情况三：一个有环、一个无环，一定不相交return null;
}private static Node getLoopNode(Node head) {Node slow = head, fast = head;do {if (fast.next == null || fast.next.next == null) {return null;}slow = slow.next;fast = fast.next.next;} while (slow != fast);// do...while 能出来，说明slow与fast相交// 将fast放回到头节点，然后快慢指针一起往下走fast = head;while (slow != fast) {slow = slow.next;fast = fast.next;}// 再次相遇的点，就是入环节点return slow;
}// 如果两个链表都无环，返回第一个相交节点，如果不相交，返回null
private static Node getIntersectWithNoLoop(Node head1, Node head2) {Node cur1 = head1, cur2 = head2;int cnt = 0; // 用于计算两个链表节点数量的差值// 找到head1的最后一个节点while (cur1.next != null) {cnt++;cur1 = cur1.next;}// 找到head2的最后一个节点while (cur2.next != null) {cnt--;cur2 = cur2.next;}// 如果最后一个节点不相等，一定不相交if (cur1 != cur2) return null;cur1 = cnt > 0 ? head1 : head2;			// 谁长，谁的头变成cur1cur2 = cur1 == head1 ? head2 : head1;	// 谁短，谁的头变成cur2cnt = Math.abs(cnt);// cur1 先走 cnt 步while (cnt-- > 0) cur1 = cur1.next;// 然后cur1、cur2一起走while (cur1 != cur2) {cur1 = cur1.next;cur2 = cur2.next;}// 相遇的点，就是相交点return cur1;
}// 如果两个链表都有环，返回第一个相交节点，如果不相交，返回null
private static Node getIntersectWithBothLoop(Node head1, Node loop1, Node head2, Node loop2) {// 1. 情况一：如果两个链表的入环节点不相等if (loop1 != loop2) {// 假设从loop1下个节点开始往下走一圈Node cur = loop1.next;while (cur != loop1) {// 如果能和loop2相遇，则找到了相交点if (cur == loop2) return loop1;cur = cur.next;}// 否则没找到相交点return null;}// 2. 情况一：如果两个链表的入环节点相等// 计算head1、head2到入环节点的节点个数差值Node cur1 = head1, cur2 = head2;int cnt = 0;while (cur1 != loop1) {cnt++;cur1 = cur1.next;}while (cur2 != loop2) {cnt--;cur2 = cur2.next;}cur1 = cnt > 0 ? head1 : head2;cur2 = cur1 == head1 ? head2 : head1;cnt = Math.abs(cnt);// cur1 先走cnt步while (cnt-- > 0) cur1 = cur1.next;// 然后cur1、cur2一起走while (cur1 != cur2) {cur1 = cur1.next;cur2 = cur2.next;}// 相遇的点，就是相交点return cur1;
}

10.2 链表删除

• 能不能不给单链表的头节点，只给想要删除的节点，就能做到在链表上把这个点删掉？

• https://leetcode.cn/problems/delete-node-in-a-linked-list/description/

  • 实际并不是真的删掉了，工程实现上不安全！！

 public void deleteNode(ListNode node) {node.val = node.next.val;node.next = node.next.next;}

10.3 二叉树先序、中序、后序的递归遍历和递归序

• 先序：任何子树的处理顺序都是，先头节点，再左子树，然后右子树；
• 中序：任何子树的处理顺序都是，先左子树，再头节点，然后右子树；
• 后序：任何子树的处理顺序都是，先左子树，再右子树，然后头节点。

// 先序打印所有节点
public static void pre(TreeNode root) {if (root == null) return;System.out.println(root.val);pre(root.left);pre(root.right);
}
// 中序打印所有节点
public static void in(TreeNode root) {if (root == null) return;in(root.left);System.out.println(root.val);in(root.right);
}
// 后序打印所有节点
public static void pos(TreeNode root) {if (root == null) return;pos(root.left);pos(root.right);System.out.println(root.val);
}

• 理解递归序
  • 先序、中序、后序都可以在递归序的基础上加工出来
  • 第一次到达一个节点就打印就是先序，第二次打印即中序，第三次即后序。

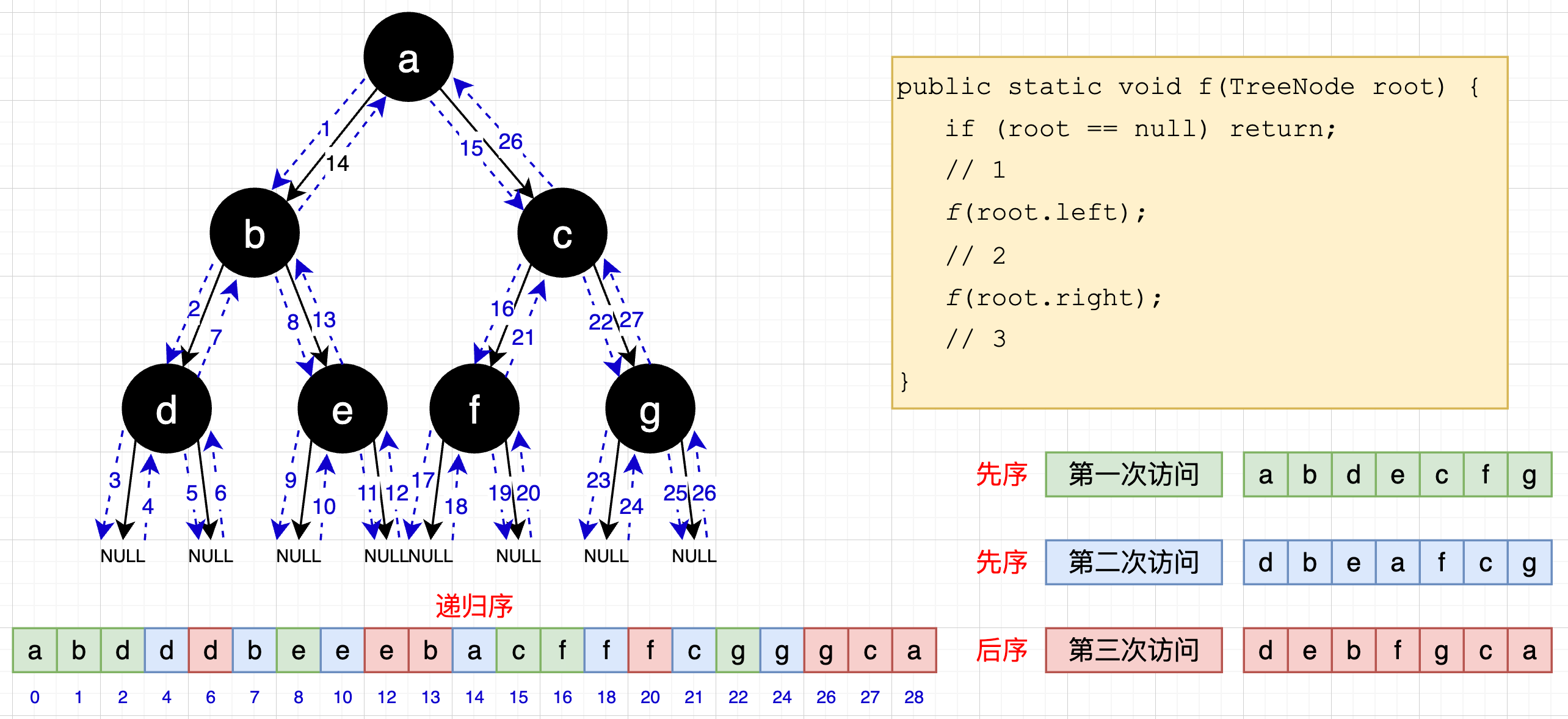
结论

• 给定一个二叉树中的节点 X，假设二叉树先序遍历中 X 左侧所有节点集合是 A，二叉树后序遍历中 X 右侧所有节点集合是 B，那么 A ∩ B 集合是 X 的所有祖先节点。

10.4 二叉树先序、中序、后序的非递归遍历

• 先序-非递归版

public static void preOrder(TreeNode root) {System.out.print("pre-order: ");if (root == null) return;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();System.out.print(node.val + " ");if (node.right != null) stack.push(node.right);if (node.left != null) stack.push(node.left);}System.out.println();
}

• 中序-非递归版

public static void inOrder(TreeNode root) {System.out.print("in-order: ");if (root == null) return;Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (!stack.isEmpty() || cur != null) {if (cur != null) {stack.push(cur);cur = cur.left;} else {cur = stack.pop();System.out.print(cur.val + " ");cur = cur.right;}}System.out.println();
}

• 后序-非递归版(1)，基于两个栈实现

public static void posOrder(TreeNode root) {System.out.print("pos-order: ");if (root == null) return;Stack<TreeNode> s1 = new Stack<>();Stack<TreeNode> s2 = new Stack<>();s1.push(root);// 先做出 `根 右 左`，压入到 s2 中while (!s1.isEmpty()) {TreeNode node = s1.pop();s2.push(node);if (node.left != null) s1.push(node.left);if (node.right != null) s1.push(node.right);}// 依次弹出 s2 中的节点，得到 `左 右 根` 后续while (!s2.isEmpty()) System.out.print(s2.pop().val + " ");System.out.println();
}

• 后序-非递归版(2)，基于一个栈实现

public static void posOrder2(TreeNode root) {System.out.print("pos-order: ");if (root == null) return;Stack<TreeNode> stack = new Stack<>();stack.push(root);TreeNode cur = root, node;while (!stack.isEmpty()) {node = stack.peek();if (node.left != null && cur != node.left && cur != node.right) stack.push(node.left);else if (node.right != null && node.right != cur) stack.push(node.right);else {System.out.print(stack.pop().val + " ");cur = node;}}System.out.println();
}

11 二叉树常见面试题和二叉树的递归套路（上）

• 内容：
  • 通过题目来熟悉二叉树的解题技巧

11.1 二叉树的按层遍历

• 层序遍历-基于队列实现，其实就是图的宽度优先遍历

public static void levelOrder(TreeNode root) {if (root == null) return;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();System.out.print(node.val + " ");if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}System.out.println();
}

• 层序遍历-基于递归

public static void levelOrder(TreeNode root, int level, List<List<Integer>> levelResults) {if (root == null) return;if (level == levelResults.size()) levelResults.add(new ArrayList<>());levelResults.get(level).add(root.val);levelOrder(root.left, level + 1, levelResults);levelOrder(root.right, level + 1, levelResults);
}

11.2 二叉树的序列化和反序列化

• 先序-序列化&反序列化

// 先序序列化
public static List<Integer> serialByPreOrder(TreeNode root) {List<Integer> result = new LinkedList<>();preOrder(root, result);return result;
}
private static void preOrder(TreeNode root, List<Integer> result) {if (root == null) result.add(null);else {result.add(root.val);preOrder(root.left, result);preOrder(root.right, result);}
}
// 先序反序列化
public static TreeNode deserialByPreOrder(List<Integer> preOrderList) {if (preOrderList == null || preOrderList.size() == 0) return null;return preOrder(preOrderList);
}
private static TreeNode preOrder(List<Integer> preOrderList) {Integer val = preOrderList.remove(0);if (val == null) return null;TreeNode root = new TreeNode(val);root.left = preOrder(preOrderList);root.right = preOrder(preOrderList);return root;
}

• 后序-序列化&反序列化

// 后序序列化
public static List<Integer> serialByPostOrder(TreeNode root) {List<Integer> result = new LinkedList<>();postOrder(root, result);return result;
}
private static void postOrder(TreeNode root, List<Integer> result) {if (root == null) result.add(