C++指针解读（3）-- 指针变量作为函数参数

函数执行是通过系统栈来实现的，系统栈分为若干个栈帧。栈帧就是函数运行的环境，每个函数在被调用时都会在系统栈区形成一个叫栈帧的结构。一次函数调用相关的数据保存在栈帧中，比如函数参数、函数的局部变量、函数执行完后的返回地址等数据。栈帧里的数据是先进后出的。

当一个函数被调用时，一个新的函数栈帧就会被创建在栈（stack）上，此时函数的参数会被压入栈中，并且执行流会跳转到被调用函数的入口。当被调用函数的执行完成后，函数栈帧会被销毁，栈指针会恢复到调用该函数之前的位置，继续执行原有函数的代码。函数栈帧的创建和销毁过程遵循“先进后出”的原则。

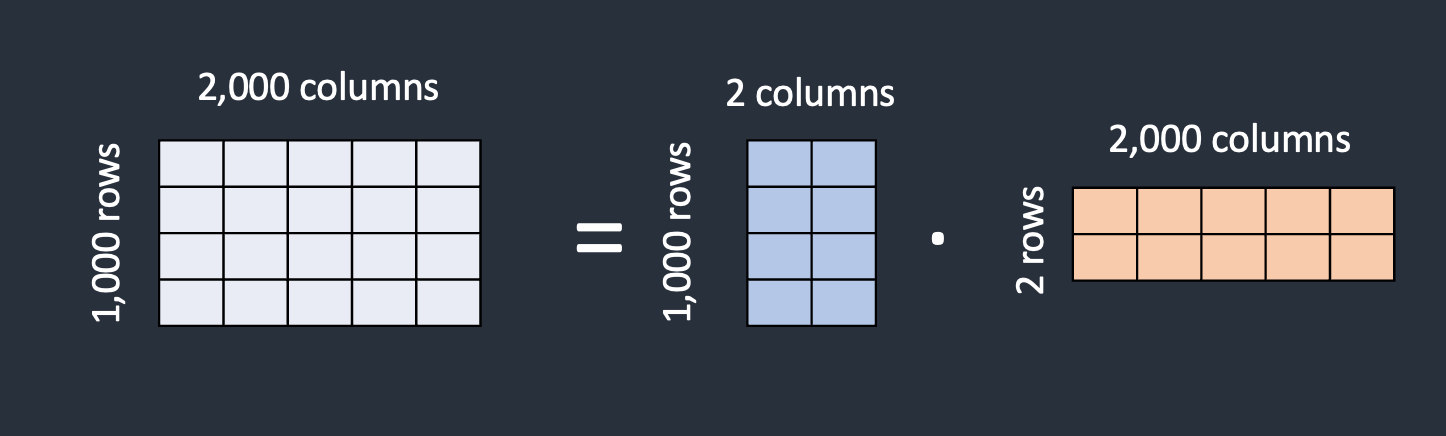
在传递参数时，传递的是它们的值（传递指针时也一样）。也就是说，在函数被调用时，函数中传递的形参其实是实参的一个副本。这样当传递的参数是一个比较大的对象时，就需要复制对象的所有字节，这会导致栈帧占用过多内存。而传递指针就不用复制这个对象，对提高系统性能有非常大的帮助。

1、用指针传递数据

1.1 在函数内部修改指针变量所指向的值

我们先来看一个用指针变量作参数的函数：

void swap(int *p1, int *p2) {int tmp;tmp = *p1;*p1 = *p2;*p2 = tmp;
}int main()
{int i1 = 5;int i2 = 7;swap(&i1, &i2);std::cout << "i1 = " << i1 << ", i2 = " << i2 << endl;return 0;
}

从执行结果看，调用swap()函数后，i1和i2的值进行了交换。

1.2 形参的指针是实参指针的一个拷贝

现在，我们把swap函数修改一下，改成直接对指针变量进行交换：

void swap(int *p1, int *p2) {int *tmp;tmp = p1;p1 = p2;p2 = tmp;
}

执行结果发现swap()函数没有起到交换作用。为什么呢？

因为在C语言中，函数参数的传递是单向的“值传递”。也就是说函数参数里的p1, p2传递的是一份指针变量的拷贝。

我们可以分别在main()和swap()函数中加入下面的代码验证p1、p2自身的地址。

void swap(int* p1, int* p2) {printf("swap():指针变量自身地址 p1:%p, p2:%p\n", &p1, &p2);... ...
}int main() {... ...printf("main():指针变量自身地址 p1:%p, p2:%p\n", &p1, &p2);... ...
}

从执行结果看，main()函数中的p1, p2地址和swap()中的p1, p2地址不同。也就是说swap()函数中的p1, p2跟main()中的p1, p2是不同的指针，虽然它们指向的地址相同。

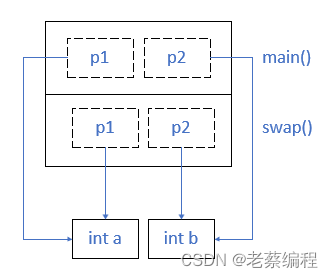
2、指针的指针

将指针传递给函数时，传递的是值。如果我们想修改原指针，就需要传递指针的指针。因为形参是一份拷贝，但不管有多少份拷贝，它永远指向原指针。

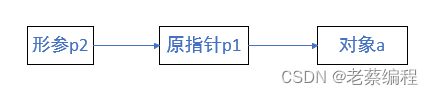
用代码表示指针的指针：

int a = 12;
int *p1 = &a;
int **p2 = &p1;

指针的指针的含义：

表达式	相当的表达式
p2	&p1 即指针p1的地址
*p2	p1, &a 即指针p1
**p2	*p1, a 即对象a

例子1：

void swap(int** p1, int** p2) {int* tmp;tmp = *p1;*p1 = *p2;*p2 = tmp;
}int main()
{int i1 = 5;int i2 = 7;int* p1 = &i1;int* p2 = &i2;swap(&p1, &p2);printf( " *p1 = %d, *p2 = %d\n", *p1, *p2);return 0;
}

例子2：

void buildArr(int **arr, int size) {*arr = (int*)malloc(size * sizeof(int));if (*arr != NULL) {for (int i = 0; i < size; i++) {*(*arr + i) = 1;}}
}
int main()
{int* arr = NULL;buildArr(&arr, 3);for (int i = 0; i < 3; i++) {printf("%d ", arr[i]);}free(arr);return 0;
}

3、用常量指针作形参

用常量指针作形参，在实际应用中还是比较多的。一是传递指针效率比传递对象值高，二是原始数据不会被修改。传递常量指针的形式如下：