M-estimators

在这里我们研究一种叫M-estimators的渐进高斯性。具体来说，如果参数估计可以用一个最小化或者最大化目标表示：

$${\theta }_o=\arg \underset{\theta \in \Theta }{\min }\mathbb{E}[q(w,\theta )]$$

比如最大似然估计就是最大化似然函数的参数，那么把样本代进去，我们就可以得到m-estimator(maximum-likelihood-like estimator Huber (1967)):

$$\hat{\theta }=\arg \underset{\theta }{\min }{N}^{-1}\sum _{i=1}^{N}q(w_i,\theta )$$

它表示就是从样本中估计的参数。
我们也可以用其极值条件来表示这个估计量，即找到其导数为0的极值点就是我们的$\hat{\theta }$：

$$N^{-1}\sum _{i=1}^N{\nabla }_{\theta }q(w_i,\hat{\theta })=0$$

这个估计方式也被称为generalized method of moments（GMM），大部分情况下GMM和MLE是等价的，GMM的适用范围会更广一点，因为那些无法用MLE的模型可以用GMM来求，比如有些数据的分布不知道，或者写不出具体的形式，这时候MLE就没法用了。

Consistency and normality of M-estimators

那么这个估计的参数$\hat{\theta }$有些什么性质呢？对于估计量的性质，我们一般关心这三个问题：可识别性（identifiability)，一致性（consistency），以及渐进高斯性（asymptotic normality）。

可识别性是基本要求，也就是这个极值点是唯一的，不可以存在另外的参数但他们的大小相同，这个性质一般是具体问题具体分析，这里先假设成立。

Consistency

对于一致性，其实就是$\hat{\theta }\stackrel{p}{\to }{\theta }_0$是否依概率收敛到到真实的${\theta }_0$上去。

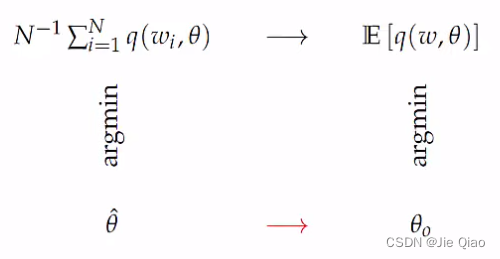
为了证明一致性，如上图，我们可以以他们的目标函数作为桥梁，通过证明$N^{-1}\sum _{i=1}^{N}q(w_i,\theta )$uniform convergence收敛到$E[q(w,\theta )]$（其实就是大数定理），并且基于${\theta }_0$的可识别性，以及连续有界等等性质，证明出$\hat{\theta }\stackrel{p}{\to }{\theta }_0$:

Normality

最后是渐进高斯性，所谓渐进高斯就是

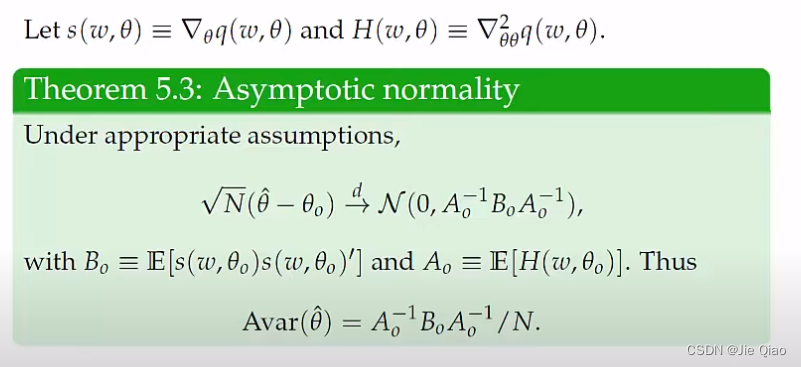
这个定理告诉我们，这个估计的参数是服从正态分布的，而且他的方差取决于q的一阶和二阶导数。这东西是怎么来的呢，其实就是通过泰勒展开建立了估计参数与目标函数导数的桥梁。具体推导如下，这里都假设可识别性以及一致性成立。

首先定义符号，$s_i(\theta )$是一个$1\times P$ 向量

$$\begin{array}{rcl}{s}_i(\theta )& \equiv & {\nabla }_{\theta }q(w_i,\theta )\\ & =& {\left(\frac{\partial q(w_i,\theta )}{\partial {\theta }_1},...,\frac{\partial q(w_i,\theta )}{\partial {\theta }_P}\right)}^T\end{array}$$

$H_i(\theta )$则是$P\times P$矩阵

$$H_i(\theta )\equiv {\nabla }_{\theta \theta }^{2}q(w_i,\theta )=\frac{{\partial }^{2}q(w_i,\theta )}{\partial \theta \partial {\theta }^{\prime }}.$$

接下来我们希望对$s_i(\theta )$作一阶泰勒展开。回顾一下泰勒展开，一个连续函数$f(x)$在$x_0$处的展开为：

$$f(x)=f(x_0)+f^{\prime }(x^{+})(x-x_0)$$

其中$x^{+}$是$x_0$和$x$之间的数，这个也称为中值定理。但如果f的输出是个向量，那么这个展开就是向量形式的泰勒展开：

$$\mathbf{f}(\mathbf{x})=\mathbf{f}({\mathbf{x}}_0)+\frac{\partial \mathbf{f}(\mathbf{x})}{\partial \mathbf{x}}{|}_{\mathbf{x}={\mathbf{x}}^{+}}(\mathbf{x}-{\mathbf{x}}_0)$$

这里$\frac{\partial \mathbf{f}(\mathbf{x})}{\partial \mathbf{x}}$是一个矩阵，对于该矩阵的每一行，其对应的${\mathbf{x}}^{+}$都是不同的。

接下来，我们建立$\theta$与$s(\theta )$的联系，具体的，把这个泰勒展开用到$s_i(\theta )$上，

$$\sum _{i=1}^N{s}_i(\hat{\theta })=\sum _{i=1}^N{s}_i({\theta }_0)+\sum _{i=1}^N\frac{\partial s_i(\theta )}{\partial \theta }{|}_{{\theta }^{+}}(\hat{\theta }-{\theta }_0)$$

现在，我们用$S(\theta )=\frac{1}{N}\sum _{i=1}^N{s}_i(\theta )=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }q(w_i,\theta )$，$S^{\prime }(\theta )=\frac{1}{N}\sum _{i=1}^N\frac{\partial s_i(\theta )}{\partial \theta }{|}_{{\theta }^{+}}=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta \theta }^{2}q(w_i,\theta )$，于是

$$S(\hat{\theta })=S({\theta }_0)+S^{\prime }\left({\theta }^{+}\right)(\hat{\theta }-{\theta }_0)$$

首先，根据$\hat{\theta }$的定义，他是通过极值点求得的，因此$S(\hat{\theta })=0$，于是

$$\begin{array}{rl}0& =S({\theta }_0)+S^{\prime }\left({\theta }^{+}\right)(\hat{\theta }-{\theta }_0)\\ \hat{\theta }-{\theta }_0& =-S^{\prime }{\left({\theta }^{+}\right)}^{-1}S({\theta }_0)\end{array}$$

接下来，希望将${\theta }^{+}$变成${\theta }_0$。基于参数的一致性$\hat{\theta }\stackrel{p}{\to }{\theta }_0$，并且进一步假设$S^{\prime }$这个函数是平滑的，那么就会有

$$\begin{array}{rl}\hat{\theta }-{\theta }_0& =-S^{\prime }({\theta }_0{)}^{-1}S({\theta }_0)+o_p(1)\\ \sqrt{N}(\hat{\theta }-{\theta }_0)& =-S^{\prime }({\theta }_0{)}^{-1}\underset{\to \mathcal{N}(0,B_0)}{\underbrace{\sqrt{N}S({\theta }_0)}}+o_p(1)\end{array}$$

这里$o_p(1)$表示这条等式在$N\to \infty$的时候成立。接下来，因为${\theta }_0$是个常数，而$S({\theta }_0)=\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }q(w_i,{\theta }_0)$，是一个样本的均值，所以根据中心极限定理，这个东西会趋于正态分布，并且因为$E[S({\theta }_0)]=0$（因为${\theta }_0$是$\mathbb{E}[q(w,\theta )]$的极值点），所以其正态分布的均值为0，而其方差则是$Var({\nabla }_{\theta }q(w_i,{\theta }_0))=Var(s_i({\theta }_0))$，记为$B_0$，并且记$A_0:=S^{\prime }({\theta }_0)$

$$\sqrt{N}(\hat{\theta }-{\theta }_0)\stackrel{d}{\to }\mathcal{N}\left(0,A_0^{-1}{B}_0{A}_0^{-1}\right)$$

这里之所以两个$A_0$是因为$-a\ast N(0,1)\sim N\left(0,a^2\right)$，是矩阵的平方的写法。最后这就是我们的定理

我们发现，这个参数估计的方差是取决于$Var({\nabla }_{\theta }q(w_i,{\theta }_0))$以及$E\left[{\nabla }_{\theta \theta }^{2}q(w_i,\theta )\right]$.

这个证明核心的地方是那个泰勒展开，其导数$S({\theta }_0)$是样本均值求和，根据中心极限定理是渐进高斯的，又因为参数$\hat{\theta }-{\theta }_0$可以用$S({\theta }_0)$表示，从而可以写出渐进高斯的表达式。

例子

考虑一个简单的线性模型

$$y=ax+ϵ,$$

其中$x\sim \mathcal{N}\left(0,{\sigma }_x^2\right),ϵ\sim \mathcal{N}\left(0,{\sigma }_{ϵ}^2\right)$。于是，

$$\begin{array}{rl}\hat{a}& =\arg \max \frac{1}{N}\sum _{i=1}^N\log p(x_i,y_i;a)\\ & =\arg \min \frac{1}{N}\sum _{i=1}^N(y_i-a{x}_i{)}^2\end{array}$$

因此，$q(x_i,y_i,a)=(y_i-a{x}_i{)}^2$,于是

$$\begin{gathered} B_0=Var({\nabla }_{a}q(x_i,y_i,a))=Var(-2(y_i-a{x}_i)x_i)=Var(-2{ϵ}_i{x}_i)=E\left[4{ϵ}_i^2{x}_i^2\right]-4E[{ϵ}_i{x}_i{]}^2=4{\sigma }_x^2{\sigma }_{ϵ}^2 \\ {A}_0=E\left[{\nabla }_{aa}^{2}q(x_i,y_i,a)\right]=E\left[2x_i^2\right]=2{\sigma }_x^2 \end{gathered}$$

于是，我们有

$$\sqrt{N}(\hat{a}-a)\stackrel{d}{\to }\mathcal{N}\left(0,\frac{{\sigma }_{ϵ}^2}{{\sigma }_x^2}\right)$$

参考资料

Consistency and normality of M-estimators
Linearity of the Integrator of Riemann-Stieltjes Integrals