Leetcode hot 100之动态规划【递推公式】

入门理解

斐波那契(Fibonacci）数列：递归

数塔：递推

递推公式

最小路径和

遍历顺序

整数拆分：拆分为和，乘积最大化

背包：：+ ->装包

框架

01背包：不可复选

倒序遍历

选择i：右下角依赖左上角，保证上一层的值不被覆盖

不选择i：dp[i][v]=dp[i-1][v]同列不受影响

一分为二，weight[i]==value[i]

最值：dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i])

分割等和子集：正整数

最后一块石头的重量II

组合数：dp[j] += dp[j - nums[i]];

目标和：非负整数、+ / -

完全背包

顺序遍历

选择i：右边依赖左边，使用的是同层的值，需要先生成左边

不选择i：dp[i][v]=...dp[i-1][v]同列不受影响

方案数：dp[i] += dp[i - nums[j]]

组合数：外层物品，内层背包

排列数：外层背包，内层物品

零钱兑换II：组合数

组合总和 Ⅳ：排列数

最少个数

零钱兑换

完全平方数

判断

单词拆分

子集：dp[i]至多i可选

最值

一和零

一分为二：weight[i]==value[i]

子序列：dp[i]以下标i - 1/i为结尾（保持相对顺序）

连续

最长回文子串

最大子序和

最长重复子数组

非连续

最长公共子序列(LCS)

不相交的线：最长公共子序列长度

不同的子序列

最长上升子序列

最长回文子序列

打家劫舍：子集+最值+不能偷连续

数组

环

二叉树

买卖股票

买卖一次

贪心：取最左最小值，取最右最大值，差值就是最大利润

在再次购买前出售掉之前

贪心：利润分解为每天

最多两笔

最多 k 笔

冷冻期

手续费

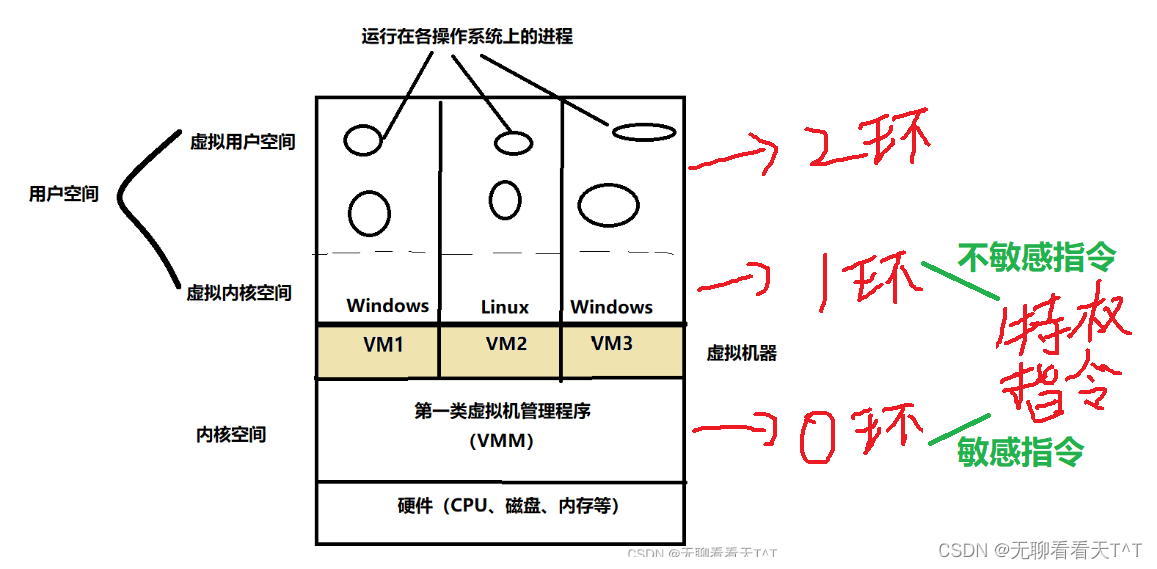
(Dynamic Programming，DP)

递归或者递推的写法来实现动态规划，其中递归写法在此处又称作记忆化搜索

入门理解

斐波那契(Fibonacci）数列：递归

function F(n){
if(n= 0||n== 1) return 1;
else return F(n-1)+F(n-2);
}

dp[n]=-1表示F(n)当前还没有被计算过

function F(n) {
if(n == 0||n==1) return 1;//递归边界
if(dp[n] != -1) return dp[n]; //已经计算过，直接返回结果，不再重复计算else {
else dp[n] = F(n-1) + F(n-2); //计算F(n)，并保存至dp[n]
return dp [n];//返回F(n)的结果
}

数塔：递推

第i层有i个数字。现在要从第一层走到第n层，最后将路径上所有数字相加后得到的和最大是多少?

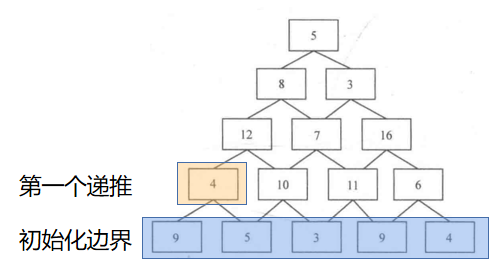
dp[i][j]表示从第i行第j个数字出发到达最底层的所有路径中能得到的最大和

dp[i][i]=max(dp[i-1][j],dp[i-1][j+1])+f[i][j]

递推公式

最小路径和

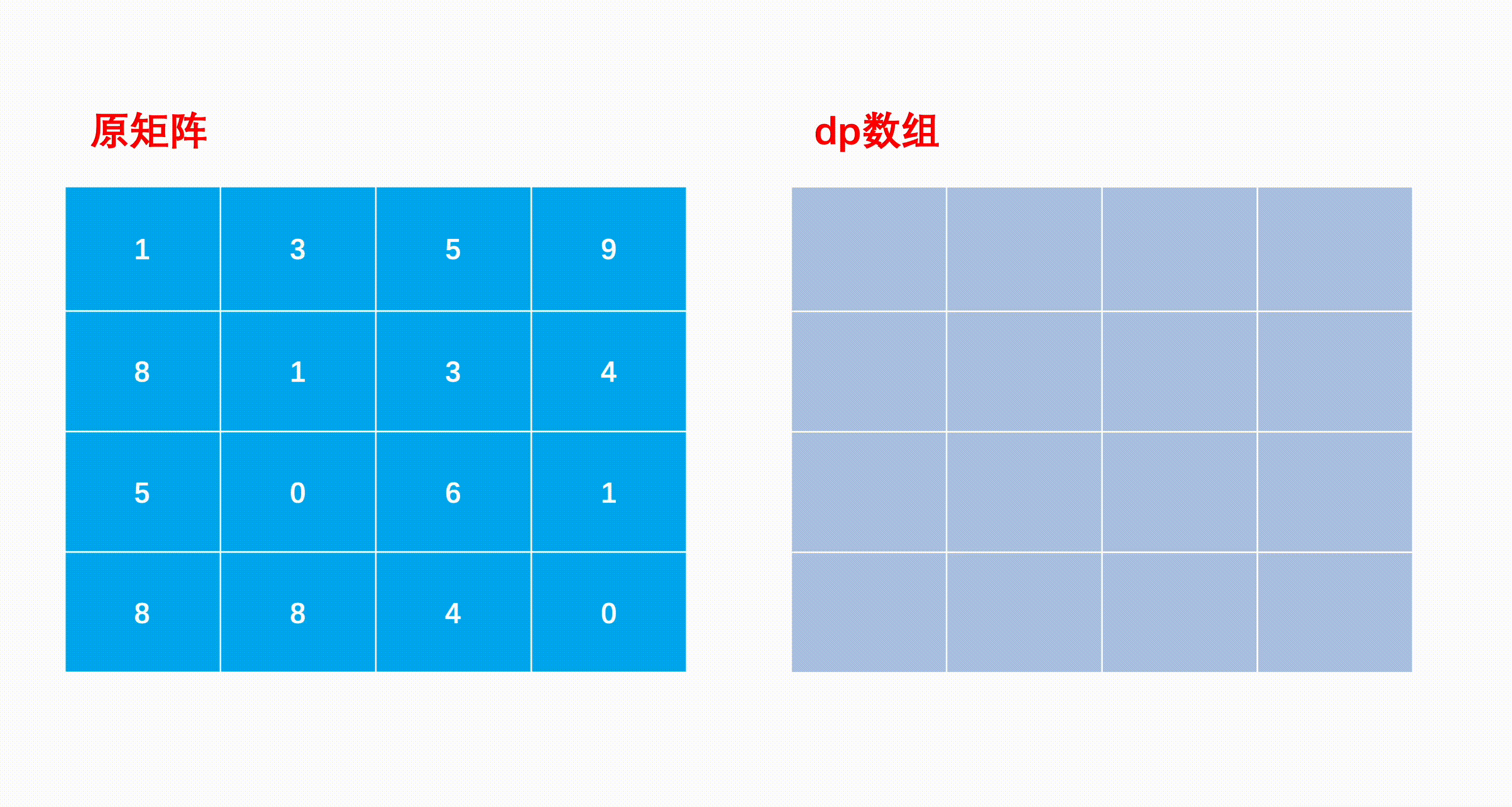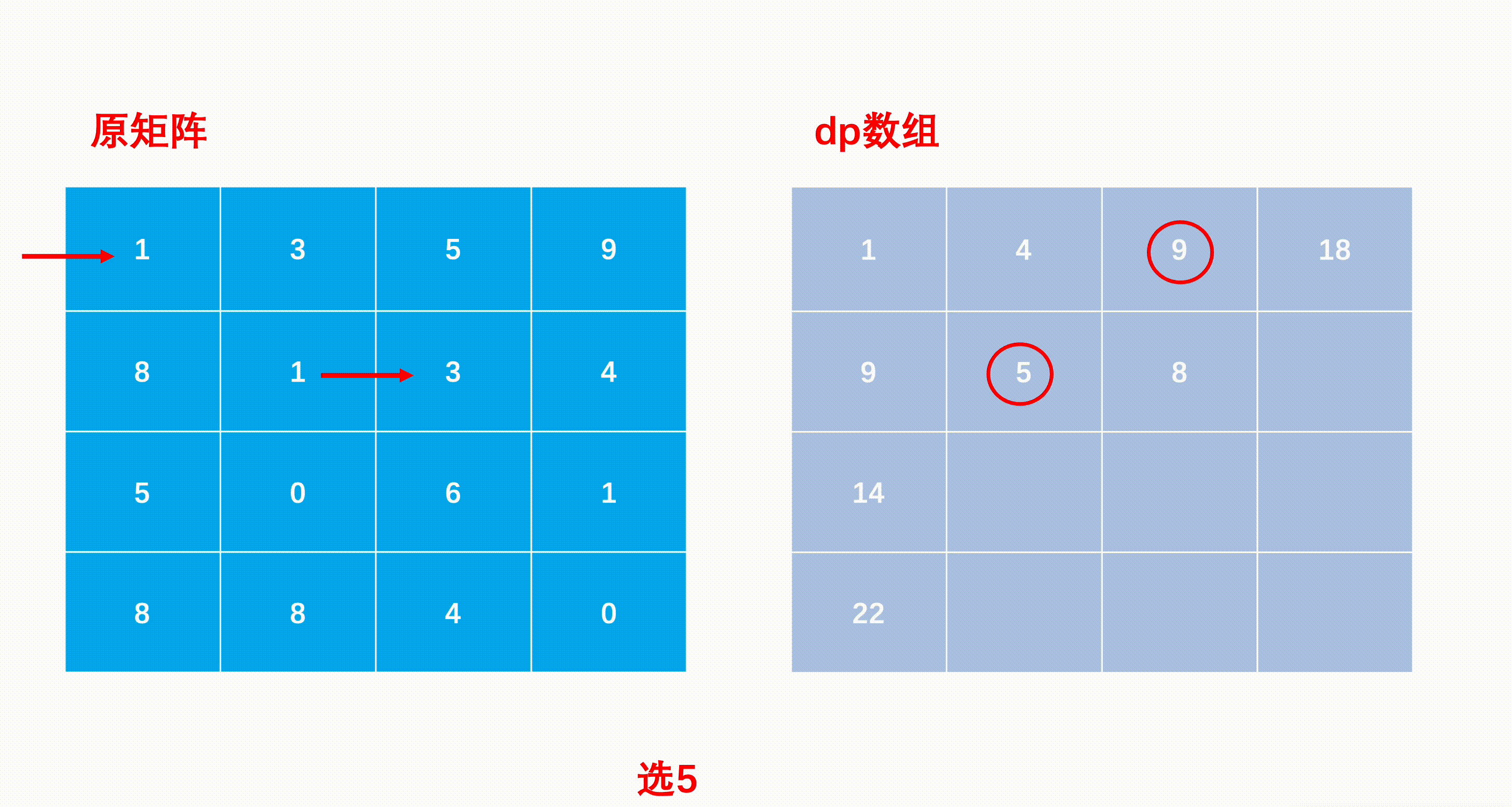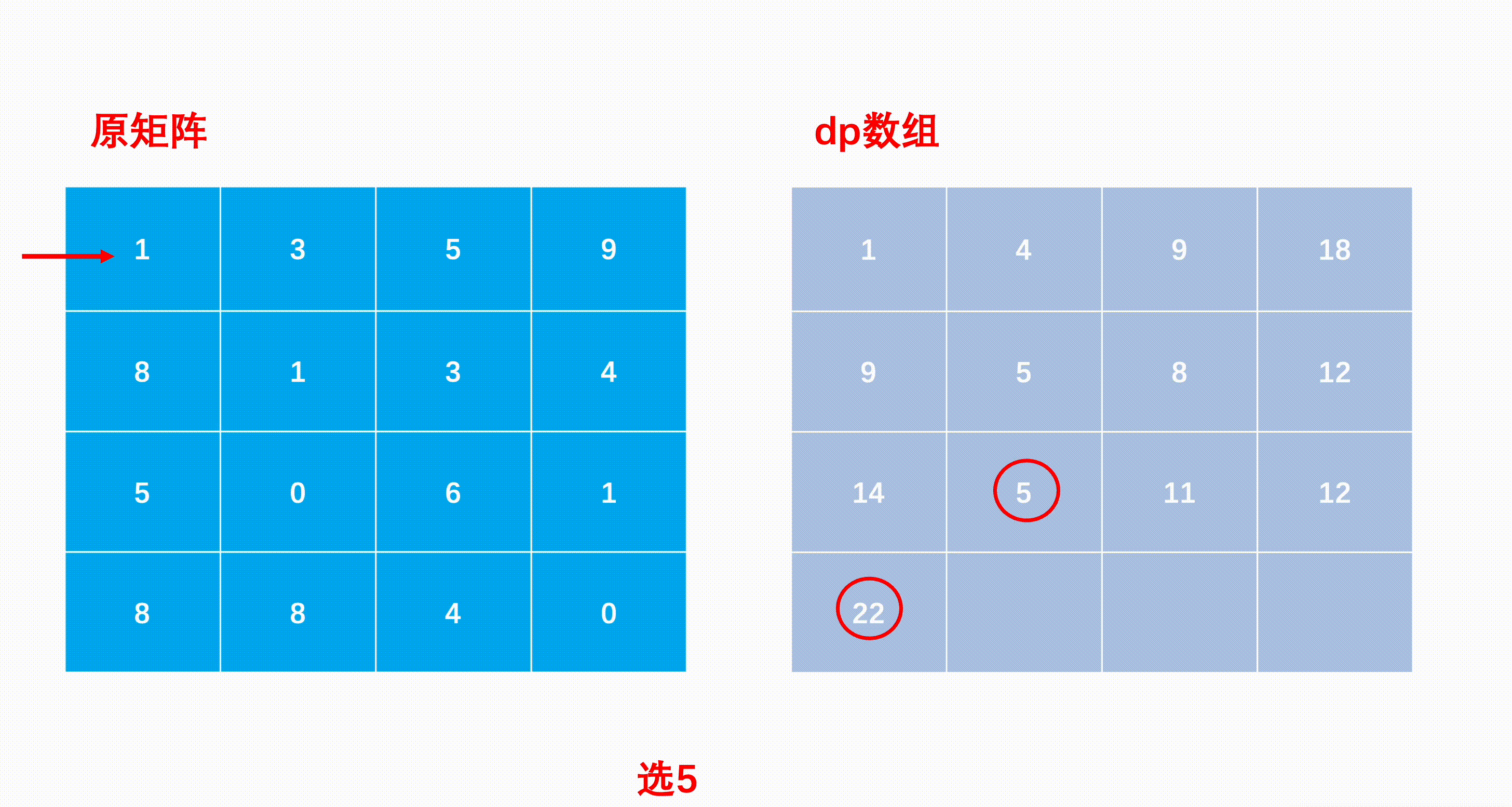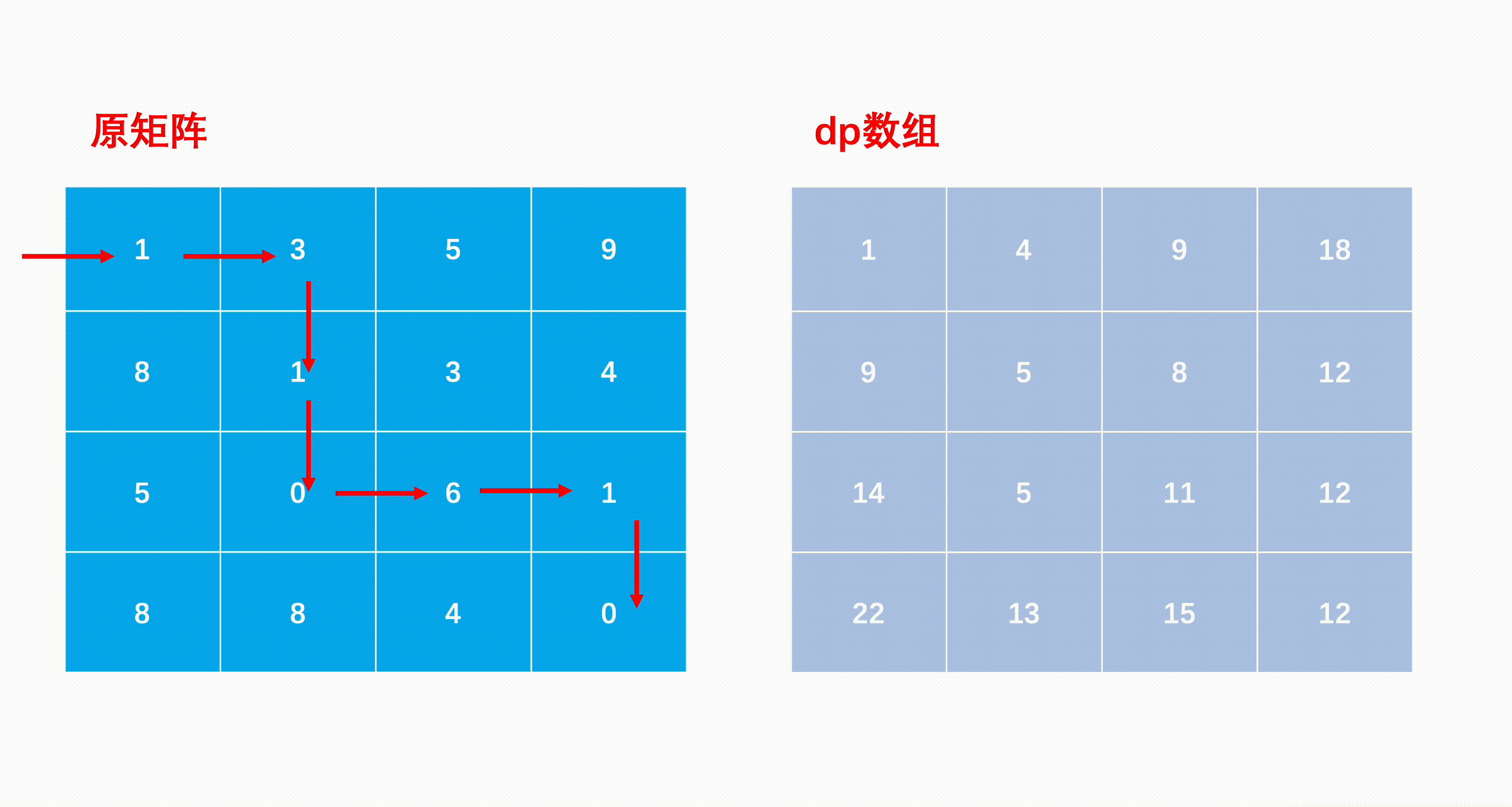
mxn矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

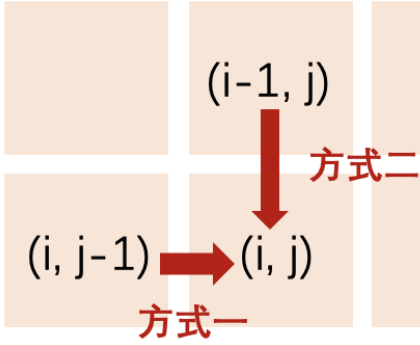dp[i][j]代表i到j的最短路径

求解子问题时的状态转移方程：从「上一状态」到「下一状态」的递推式。

dp[i, j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j]

JavaScript中没有二维数组的概念，但是可以设置数组元素的值等于数组

key：

dp[0][i] = dp[0][i - 1] + matrix[0][i];
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];

function minPathSum(matrix) {var row = matrix.length,col = matrix[0].length;var dp = new Array(row).fill(null).map(() => new Array(col).fill(0));dp[0][0] = matrix[0][0]; // 初始化左上角元素// 初始化第一行for (var i = 1; i < col; i++) dp[0][i] = dp[0][i - 1] + matrix[0][i];// 初始化第一列for (var j = 1; j < row; j++) dp[j][0] = dp[j - 1][0] + matrix[j][0];// 动态规划for (var i = 1; i < row; i++) {for (var j = 1; j < col; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];}}return dp[row - 1][col - 1]; // 右下角元素结果即为答案
}

遍历顺序

整数拆分：拆分为和，乘积最大化

其实可以从1遍历j，然后有两种渠道得到dp[i].

拆分为2个数：是j * (i - j) 直接相乘。

拆分为3个及以上个数：j * dp[i - j]，相当于是拆分(i - j)

dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]

var integerBreak = function(n) {let dp = new Array(n + 1).fill(0)dp[2] = 1for(let i = 3; i <= n; i++) {for(let j = 1; j <= i / 2; j++) {dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)}}return dp[n]
};

背包：：+ ->装包

框架

for 状态1 in 状态1的所有取值：for 状态2 in 状态2的所有取值：for ...dp[状态1][状态2][...] = 择优(选择1，选择2...)int dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0for i in [1..N]:for w in [1..W]:dp[i][w] = max(把物品 i 装进背包,不把物品 i 装进背包)
return dp[N][W]...加上边界条件，装不下的时候，只能选择不装

01背包：不可复选

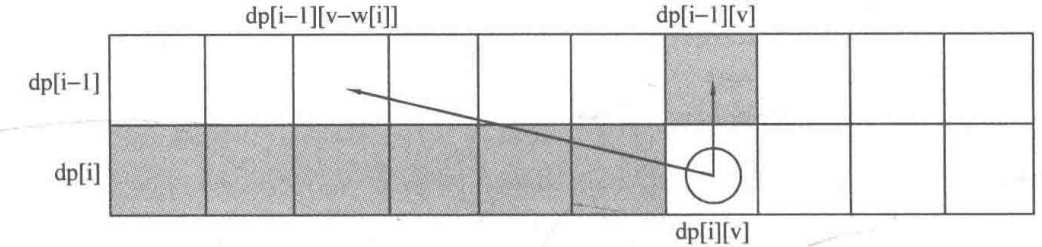
n件物品,重量为w[i],价值为c[j]，容量为V的，其中每种物品都只有1件。
dp[i][v]表示前i件物品(1≤i≤n, 0≤v≤V)恰好装入容量为v的背包中所能获得的最大价值。

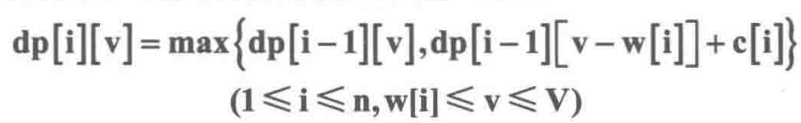
function testWeightBagProblem (weight, value, size) {// 定义 dp 数组const len = weight.length,dp = Array(len).fill().map(() => Array(size + 1).fill(0));// 初始化for(let j = weight[0]; j <= size; j++) {dp[0][j] = value[0];}// weight 数组的长度len 就是物品个数for(let i = 1; i < len; i++) { // 遍历物品for(let j = 0; j <= size; j++) { // 遍历背包容量if(j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}console.table(dp)return dp[len - 1][size];
}function test () {console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}test();

倒序遍历

选择i：右下角依赖左上角，保证上一层的值不被覆盖

不选择i：dp[i][v]=dp[i-1][v]同列不受影响

本质上还是一个对二维数组的遍历，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。

for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}

一分为二，weight[i]==value[i]

如果使用一维dp数组，物品（value）遍历的for循环放在外层，遍历背包（weight）的for循环放在内层，且内层for循环倒序遍历！滚动数组

最值：dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i])

分割等和子集：正整数

背包的体积为sum / 2
背包要放入的商品（集合里的元素）重量为元素的数值，价值也为元素的数值
背包如果正好装满，说明找到了总和为 sum / 2 的子集。
背包中每一个元素是不可重复放入。

var canPartition = function(nums) {const sum = (nums.reduce((p, v) => p + v));
//奇数if (sum & 1) return false;const dp = Array(sum / 2 + 1).fill(0);for(let i = 0; i < nums.length; i++) {for(let j = sum / 2; j >= nums[i]; j--) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);if (dp[j] === sum / 2) {return true;}}}return dp[sum / 2] === sum / 2;
};

最后一块石头的重量II

/*** @param {number[]} stones* @return {number}*/
var lastStoneWeightII = function (stones) {let sum = stones.reduce((s, n) => s + n);let dpLen = Math.floor(sum / 2);let dp = new Array(dpLen + 1).fill(0);for (let i = 0; i < stones.length; ++i) {for (let j = dpLen; j >= stones[i]; --j) {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - dp[dpLen] - dp[dpLen];
};

组合数：dp[j] += dp[j - nums[i]];

目标和：非负整数、+ / -

left组合 - right组合 = target。

left + right = sum，而sum是固定的。right = sum - left

公式来了， left - (sum - left) = target 推导出 left = (target + sum)/2 。

target是固定的，sum是固定的，left就可以求出来。

此时问题就是在集合nums中找出和为left的组合

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。

例如：dp[j]，j 为5，

已经有一个1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把所有的 dp[j - nums[i]] 累加起来。

所以求组合类问题的公式，都是类似这种：

dp[j] += dp[j - nums[i]]

const findTargetSumWays = (nums, target) => {const sum = nums.reduce((a, b) => a+b);if(Math.abs(target) > sum) {return 0;}if((target + sum) % 2) {return 0;}const halfSum = (target + sum) / 2;let dp = new Array(halfSum+1).fill(0);dp[0] = 1;for(let i = 0; i < nums.length; i++) {for(let j = halfSum; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[halfSum];
};

完全背包

与01背包问题不同的是其中每种物品都有无数件。

顺序遍历

选择i：右边依赖左边，使用的是同层的值，需要先生成左边

不选择i：dp[i][v]=...dp[i-1][v]同列不受影响

// 先遍历物品，再遍历背包容量
function test_completePack1() {let weight = [1, 3, 5]let value = [15, 20, 30]let bagWeight = 4 let dp = new Array(bagWeight + 1).fill(0)for(let i = 0; i <= weight.length; i++) {for(let j = weight[i]; j <= bagWeight; j++) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])}}console.log(dp)
}// 先遍历背包容量，再遍历物品
function test_completePack2() {let weight = [1, 3, 5]let value = [15, 20, 30]let bagWeight = 4 let dp = new Array(bagWeight + 1).fill(0)for(let j = 0; j <= bagWeight; j++) {for(let i = 0; i < weight.length; i++) {if (j >= weight[i]) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])}}}console.log(2, dp);
}

完全背包的两个for循环的先后顺序都是可以的。

方案数：dp[i] += dp[i - nums[j]]

组合数：外层物品，内层背包

for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}

假设：coins[0] = 1，coins[1] = 5。

先把1加入计算，再把5加入计算，得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况

排列数：外层背包，内层物品

for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}

背包容量的每一个值，都是经过 1 和 5 的计算，包含了{1, 5} 和 {5, 1}两种情况。

dp[j]在外层，遇到1时更新了一次5，遇到5时更新了一次1

零钱兑换II：组合数

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

输入: amount = 5, coins = [1, 2, 5]
输出: 4

解释: 有四种方式可以凑成总金额:

5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

const change = (amount, coins) => {let dp = Array(amount + 1).fill(0);dp[0] = 1;for(let i =0; i < coins.length; i++) {for(let j = coins[i]; j <= amount; j++) {dp[j] += dp[j - coins[i]];}}return dp[amount];
}

组合总和 Ⅳ：排列数

爬楼梯

const combinationSum4 = (nums, target) => {let dp = Array(target + 1).fill(0);dp[0] = 1;for(let i = 0; i <= target; i++) {for(let j = 0; j < nums.length; j++) {if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];
};

最少个数

零钱兑换

纯完全背包求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！

// 遍历物品
const coinChange = (coins, amount) => {if(!amount) {return 0;}let dp = Array(amount + 1).fill(Infinity);dp[0] = 0;for(let i = 0; i < coins.length; i++) {for(let j = coins[i]; j <= amount; j++) {dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);}}return dp[amount] === Infinity ? -1 : dp[amount];
}

完全平方数

完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，问凑满这个背包最少有多少物品？

for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}

判断

单词拆分

单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。

拆分时可以重复使用字典中的单词，说明就是一个完全背包！

dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

const wordBreak = (s, wordDict) => {let dp = Array(s.length + 1).fill(false);dp[0] = true;for(let i = 0; i <= s.length; i++){for(let j = 0; j < wordDict.length; j++) {if(i >= wordDict[j].length) {if(s.slice(i - wordDict[j].length, i) === wordDict[j] && dp[i - wordDict[j].length]) {dp[i] = true}}}}return dp[s.length];
}

子集：dp[i]至多i可选

最值

一和零

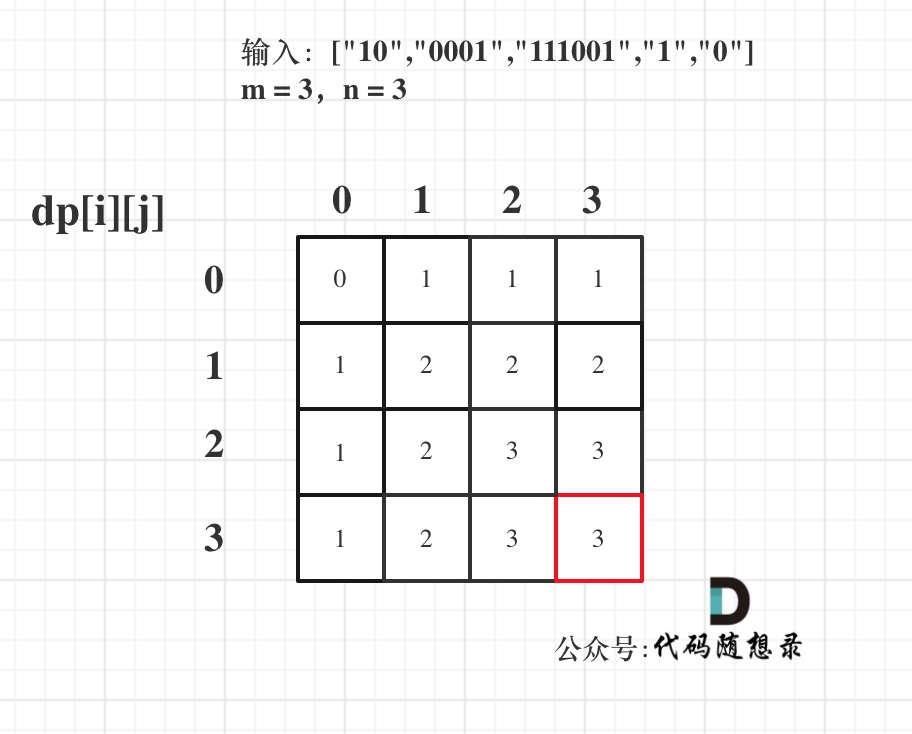
找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1 。

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

确定递推公式

dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取dp[i][j]的最大值。

所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]）

const findMaxForm = (strs, m, n) => {const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));let numOfZeros, numOfOnes;for(let str of strs) {numOfZeros = 0;numOfOnes = 0;for(let c of str) {if (c === '0') {numOfZeros++;} else {numOfOnes++;}}for(let i = m; i >= numOfZeros; i--) {for(let j = n; j >= numOfOnes; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - numOfZeros][j - numOfOnes] + 1);}}}return dp[m][n];
};

一分为二：weight[i]==value[i]

子序列：dp[i]以下标i - 1/i为结尾（保持相对顺序）

for(let i = 1; i < nums.length; i++)
for(let j = 0; j < i; j++)

连续

最长回文子串

dp[i][j]表示S[i]至S[j]所表示的子串是否是回文子串，是则为1，不是为0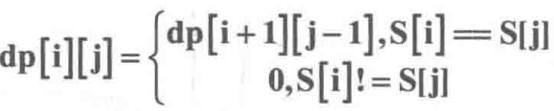

最大子序和

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

dp[i] = max(dp[i - 1] + nums[i], nums[i]);

最长重复子数组

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。

当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;

动态规划

const findLength = (A, B) => {// A、B数组的长度const [m, n] = [A.length, B.length];// dp数组初始化，都初始化为0const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));// 初始化最大长度为0let res = 0;for (let i = 1; i <= m; i++) {for (let j = 1; j <= n; j++) {// 遇到A[i - 1] === B[j - 1]，则更新dp数组if (A[i - 1] === B[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}// 更新resres = dp[i][j] > res ? dp[i][j] : res;}}// 遍历完成，返回resreturn res;
};

滚动数组

const findLength = (nums1, nums2) => {let len1 = nums1.length, len2 = nums2.length;// dp[i][j]: 以nums1[i-1]、nums2[j-1]为结尾的最长公共子数组的长度let dp = new Array(len2+1).fill(0);let res = 0;for (let i = 1; i <= len1; i++) {for (let j = len2; j > 0; j--) {if (nums1[i-1] === nums2[j-1]) {dp[j] = dp[j-1] + 1;} else {dp[j] = 0;}res = Math.max(res, dp[j]);}}return res;
}

非连续

最长公共子序列(LCS)

Longest Common Subsequence：子序列可以不连续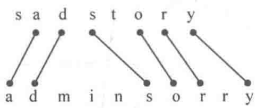
“sadstory”与“adminsorry”最长公共子序列为“adsory”

dp[i][j]：strA[i]和strB[j]之前的LCS 长度，下标从1开始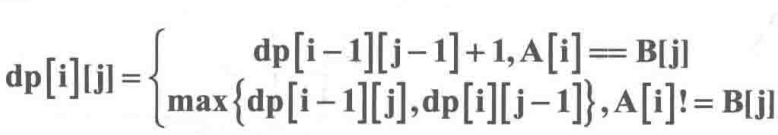

不相交的线：最长公共子序列长度

直线不能相交，这就是说明在字符串A中找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

不同的子序列

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]

const numDistinct = (s, t) => {let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));for(let i = 0; i <=s.length; i++) {dp[i][0] = 1;}for(let i = 1; i <= s.length; i++) {for(let j = 1; j<= t.length; j++) {if(s[i-1] === t[j-1]) {
//不用s[i - 1]来匹配，个数为dp[i - 1][j]dp[i][j] = dp[i-1][j-1] + dp[i-1][j];} else {dp[i][j] = dp[i-1][j]}}}return dp[s.length][t.length];
};

最长上升子序列

dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

const lengthOfLIS = (nums) => {let dp = Array(nums.length).fill(1);let result = 1;for(let i = 1; i < nums.length; i++) {for(let j = 0; j < i; j++) {if(nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j]+1);}}result = Math.max(result, dp[i]);}return result;
};

最长回文子序列

const longestPalindromeSubseq = (s) => {const strLen = s.length;let dp = Array.from(Array(strLen), () => Array(strLen).fill(0));for(let i = 0; i < strLen; i++) {dp[i][i] = 1;}for(let i = strLen - 1; i >= 0; i--) {for(let j = i + 1; j < strLen; j++) {if(s[i] === s[j]) {dp[i][j] = dp[i+1][j-1] + 2;} else {dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][strLen - 1];
};

打家劫舍：子集+最值+不能偷连续

数组

dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。

决定dp[i]的因素就是第i房间偷还是不偷。

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。

如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

环

受影响的是首尾元素

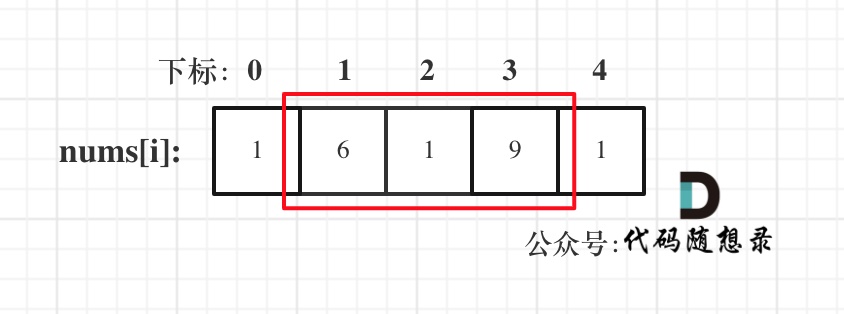
对于一个数组，成环的话主要有如下三种情况：

情况一：考虑不包含首尾元素=线性数组

213.打家劫舍II

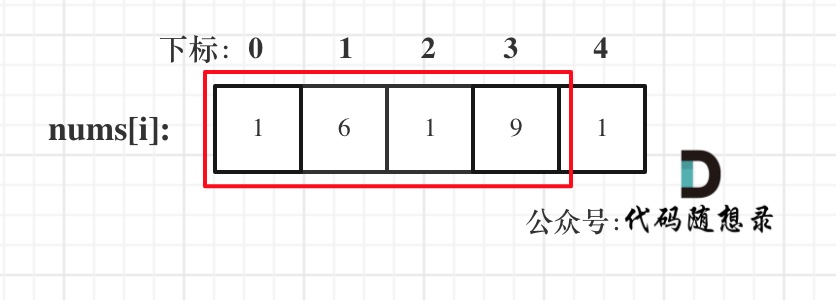
情况二：考虑包含首元素，不包含尾元素

213.打家劫舍II1

情况三：考虑包含尾元素，不包含首元素

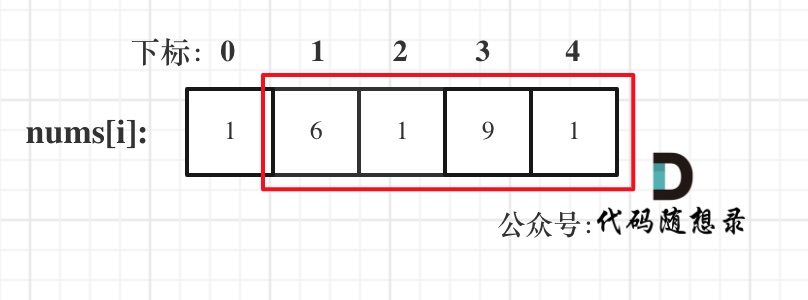
213.打家劫舍II2

注意我这里用的是"考虑"，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！对于情况三，取nums[1] 和 nums[3]就是最大的。

而情况二和情况三都包含了情况一了，所以只考虑情况二和情况三就可以了。

var rob = function(nums) {const n = nums.lengthif (n === 0) return 0if (n === 1) return nums[0]const result1 = robRange(nums, 0, n - 2)const result2 = robRange(nums, 1, n - 1)return Math.max(result1, result2)
};const robRange = (nums, start, end) => {if (end === start) return nums[start]const dp = Array(nums.length).fill(0)dp[start] = nums[start]dp[start + 1] = Math.max(nums[start], nums[start + 1])for (let i = start + 2; i <= end; i++) {dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])}return dp[end]
}

二叉树

下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。

所以本题dp数组就是一个长度为2的数组！

那么有同学可能疑惑，长度为2的数组怎么标记树中每个节点的状态呢？

别忘了在递归的过程中，系统栈会保存每一层递归的参数。

后序遍历：通过递归函数的返回值来做下一步计算

const rob = root => {// 后序遍历函数const postOrder = node => {// 递归出口if (!node) return [0, 0];// 遍历左子树const left = postOrder(node.left);// 遍历右子树const right = postOrder(node.right);// 不偷当前节点，左右子节点都可以偷或不偷，取最大值const DoNot = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);// 偷当前节点，左右子节点只能不偷const Do = node.val + left[0] + right[0];// [不偷，偷]return [DoNot, Do];};const res = postOrder(root);// 返回最大值return Math.max(...res);
};

买卖股票

买卖一次

首先设定是现金为0，买股票会花钱(变成负数)，卖股票会赚钱
每一天的股票都有两种状态分别是持有和不持有
对于递推公式dp【i】【0】 = max(dp【i - 1】【0】, -price【i】)来说，
其实就是买不买第i天这支股票,买的话金钱减少，不买就维持前一天的状态，在买和不买两种情况中取剩钱最多的那个
对于dp【i】【1】 = max(dp【i - 1】【1】, dp【i - 1】【0】 + price【i】)
就是卖不卖第i天这支股票，卖的话赚钱，不卖就维持前一天的状态，在卖和不卖中取剩钱最多的那个，如果想要卖股票的话，之前必须要买过股票，所以是dp【i - 1】【0】 + price【i】

贪心：取最左最小值，取最右最大值，差值就是最大利润

int maxProfit(vector<int>& prices) {int low = INT_MAX;int result = 0;for (int i = 0; i < prices.size(); i++) {low = min(low, prices[i]);  // 取最左最小价格result = max(result, prices[i] - low); // 直接取最大区间利润}return result;}

在再次购买前出售掉之前

const maxProfit = (prices) => {let dp = Array.from(Array(prices.length), () => Array(2).fill(0));// dp[i][0] 表示第i天持有股票所得现金。// dp[i][1] 表示第i天不持有股票所得最多现金dp[0][0] = 0 - prices[0];dp[0][1] = 0;for (let i = 1; i < prices.length; i++) {// 如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来// 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]// 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);// 在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来// 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]// 第i天卖出股票，所得现金就是按照今天股票佳价格卖出后所得现金即：prices[i] + dp[i - 1][0]dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[prices.length - 1][1];
};

贪心：利润分解为每天

假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑

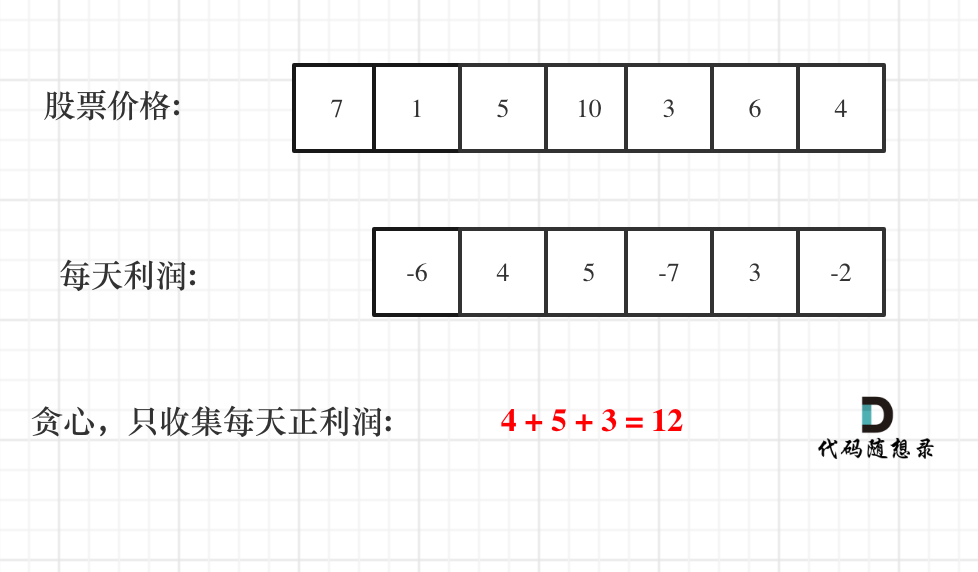
var maxProfit = function(prices) {let result = 0for(let i = 1; i < prices.length; i++) {result += Math.max(prices[i] - prices[i - 1], 0)}return result
};

最多两笔

确定dp数组以及下标的含义

一天一共就有五个状态，

没有操作（其实我们也可以不设置这个状态）
第一次持有股票
第一次不持有股票
第二次持有股票
第二次不持有股票

dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金

确定递推公式

达到dp[i][1]状态，有两个具体操作：

操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]

那么dp[i][1]究竟选 dp[i-1][0] - prices[i]，还是dp[i - 1][1]呢？

一定是选最大的，所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);

同理dp[i][2]也有两个操作：

操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]

所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])

同理可推出剩下状态部分：

dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);

dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

dp数组如何初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？其实大家可以理解当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;

最多 k 笔

0 表示不操作
1 第一次买入
2 第一次卖出
3 第二次买入
4 第二次卖出
.....

除了0以外，偶数就是卖出，奇数就是买入。

题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了

// 方法一：动态规划
const maxProfit = (k,prices) => {if (prices == null || prices.length < 2 || k == 0) {return 0;}let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0));for (let j = 1; j < 2 * k; j += 2) {dp[0][j] = 0 - prices[0];}for(let i = 1; i < prices.length; i++) {for (let j = 0; j < 2 * k; j += 2) {dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);}}return dp[prices.length - 1][2 * k];
};// 方法二：动态规划+空间优化
var maxProfit = function(k, prices) {let n = prices.length;let dp = new Array(2*k+1).fill(0);// dp 买入状态初始化for (let i = 1; i <= 2*k; i += 2) {dp[i] = - prices[0];}for (let i = 1; i < n; i++) {for (let j = 1; j < 2*k+1; j++) {// j 为奇数：买入状态if (j % 2) {dp[j] = Math.max(dp[j], dp[j-1] - prices[i]);} else {// j为偶数：卖出状态dp[j] = Math.max(dp[j], dp[j-1] + prices[i]);}}}return dp[2*k];
};

冷冻期

四个状态：

状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
不持有股票状态，这里就有两种卖出股票状态
- 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
- 状态三：今天卖出股票
状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
操作二：今天买入了，有两种情况
- 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]

那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

操作一：前一天就是状态二
操作二：前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][3] = dp[i - 1][2];

综上分析，递推代码如下：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];

手续费

// 贪心思路
var maxProfit = function(prices, fee) {let result = 0let minPrice = prices[0]for(let i = 1; i < prices.length; i++) {if(prices[i] < minPrice) {minPrice = prices[i]}if(prices[i] >= minPrice && prices[i] <= minPrice + fee) {continue}if(prices[i] > minPrice + fee) {result += prices[i] - minPrice - fee// 买入和卖出只需要支付一次手续费minPrice = prices[i] -fee}}return result
};// 动态规划
/*** @param {number[]} prices* @param {number} fee* @return {number}*/
var maxProfit = function(prices, fee) {// 滚动数组// have表示当天持有股票的最大收益// notHave表示当天不持有股票的最大收益// 把手续费算在买入价格中let n = prices.length,have = -prices[0]-fee,   // 第0天持有股票的最大收益notHave = 0;             // 第0天不持有股票的最大收益for (let i = 1; i < n; i++) {// 第i天持有股票的最大收益由两种情况组成// 1、第i-1天就已经持有股票，第i天什么也没做// 2、第i-1天不持有股票，第i天刚买入have = Math.max(have, notHave - prices[i] - fee);// 第i天不持有股票的最大收益由两种情况组成// 1、第i-1天就已经不持有股票，第i天什么也没做// 2、第i-1天持有股票，第i天刚卖出notHave = Math.max(notHave, have + prices[i]);}// 最后手中不持有股票，收益才能最大化return notHave;
};