前言

感知机是由美国学者1957年提出来，作为神经网络的起源算法。因此学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。

严格的来讲，感知机因该称为人工神经元或者朴素感知机。

什么是感知机

感知机接收多个信号输入，输出一个信号。

介绍一个接收两个输入信号的感知机的例子

x1、x2是输入信号，y是输出信号，w1、w2是权重。图中的⭕成为“神经元”。输入信号被送到神经元时，乘固定的权重（w1x1、w2x2）。神经元会计算传送过来的信号的总和，只有总和超过某个界限制时，才会输出1，也成为“神经元被激活”。界限值称为阈值，使用符号θ

感知机的运行原理只有这些！！！

公式表达：

$$y=\{\begin{array}{l}0，(w1x1+w2x2)\le \theta \\ 1，(w1x1+w2x2)>\theta \end{array}$$
感知机的多个输入信号都有各自的权重值，这些权重发挥着控制各个信号的重要性，权重越大，对应的信号就越强烈！！！！

接下来用感知机来解决简单问题……

简单的逻辑电路

与门

与门仅在两个输入均为1时输出1，其他情况为0。

x1	x2	y
0	0	0
0	1	0
1	0	0
1	1	1

下面考虑使用感知机实现。需要做的就是能满足上表。

实际上，满足上表中的条件需要参数的选择，参数的选择有无数个，比如当（w1,w2,θ）=(1.0,1.0,1.0)时可以满足与门的条件。

与非门和或门

与非门就是颠倒了与门的输出，仅当x1和x2同时为1时输出0，其他情况为1。

x1	x2	y
0	0	1
0	1	1
1	0	1
1	1	0

与非门的参数组合？其实就是把与门的参数符号取反就可以。

如当（w1,w2,θ）=(-1.0,-1.0,-1.0)时可以满足与非门的条件。

或门只要有一个输入信号是1时，输出就为1

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	1

这里决定感知机参数的并不是计算机，而是我们人，真值表中的数据类似于“训练数据”，我们想到参数的值。但是在机器学习中这个参数的决定是由计算机自动进行。学习是确定合适参数的过程，而人要做的是思考感知机的构造模型，把训练数据交给计算机。

与门、与非门、或门的感知机构造是一样的，只是需要合适的调整参数

感知机的实现

简单的实现

定义一个接收参数的AND函数，在函数内初始化参数w1、w2、theta，当输入的加权总和超过阈值时返回1， 否则返回0。

def AND(x1, x2):w1, w2, theta = 0.5, 0.5, 0.7tmp = x1 * w1 + x2 * w2if tmp <= theta:return 0else:return 1
result = AND(0, 1)
print(result)

导入权重和偏置

修改为另外一种实现形式，把θ换成-b，于是形成一种公式
$$y=\{\begin{array}{l}0，(b+w1x1+w2x2)\le 0\\ 1，(b+w1x1+w2x2)>0\end{array}$$
虽然符号不相同，但是内容完全相同，b成为偏置，w1和w2称为权重，感知机会计算输入信号和权重的乘积，再加上偏置。

import numpy as  np
x = np.array([0,1]) # [0 1]
w = np.array([0.5,0.5])
b = -0.7
print(np.sum(w*x)+b)

在NumPy数组的乘法运算中，当两个数组的元素个数相同时， 各个元素分别相乘。

因此wx的结果就是它们的各个元素分别相乘（[0, 1] * [0.5, 0.5] => [0, 0.5]），之后，np.sum(wx)再计算相乘后的各个元素的总和。

这里把**-θ叫为偏置为b**,注意偏置和权重w1，w2的作用不一样。具体的说w1和w2是控制输入信号的重要参数，而偏置是调整神经元被激活的容易程度的参数。比如b为-0.1时，则只需要输入信号的加权总和超过0.1，神经元就会被激活。偏置的值决定了神经元被激活的容易程度。

感知机的局限性

异或门

x1和x2二者不一样时输出1

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	0

实际上，前面介绍的感知机是无法实现这个异或门的。

为什么可以使用感知机实现与门，与非门和或门，但是无法实现异或门的？

再或门的情况下，权重（b,w1,w2）=（-0.5，1.0，1.0）时，此时感知机可用下面表示
$$y=\{\begin{array}{l}0，(-0.5+x1+x2)\le 0\\ 1，(-0.5+x1+x2)>0\end{array}$$

由直线-0.5+x1+x2=0分割开的两个空间。一个空间输出1，一个空间输出0。如果制作或门，需要用直线将上图的○和△分开。实际上，直线就将这四个点正确分开了。

想要用一条直线是无法将○和△分开。

线性和非线性

在异或门中，无法用一条直线分开，但是如果将这个“直线”限制条件去除。

感知机的局限性就在于只能由一条直线分割的空间，下图的曲线无法用感知机表示。

**直线分割的空间称为线性空间。曲线分割的为非线性空间。**线性、非线性在机器学习领域中很常见

多层感知机

实际上，感知机可以进行叠加，在单层感知机中，不能对异或进行表示，但是多层感知机可以进行表示。

已有门电路的组合

要实现异或门，要对与门，与非门，或门进行配置。

严格的来讲，单层感知机无法表示异或门或者无法分离非线性空间，接下来我们可以通过多层感知机来实现异或门。

通过与门，与非门，或门组合进行表示异或门。

异或门的实现

# 异或门的实现
def XOR(x1, x2):s1 = OR(x1, x2)s2 = NAND(x1, x2)return AND(s1, s2)
result = XOR(1,1)
print(result)

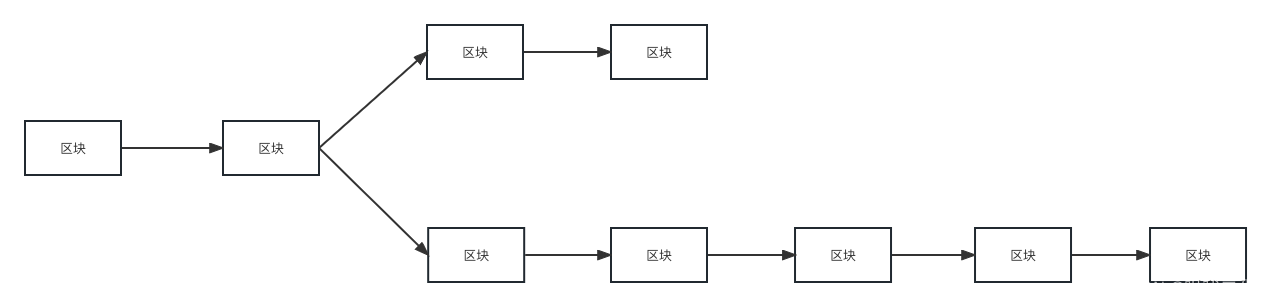
异或门是一种多层结构的神经网络。最左边的从第0层开始，前面介绍的与门，与非门，或门为单层感知机，异或门为多层感知机。

在上图中的两层感知机中，现在第0层和第1层的神经元之间进行信号的传送和接收，然后再第1层和第2层进行信号的传送和接收。

1.在第0层的两个神经元接收输入信号，并将信号发送到第1层的神经元。

2.第1层的神经元将信号发送到第2层，第二层的神经元输出y

感知机的叠加能够进行非线性的表示

代码合集

# 与门的实现
def AND(x1, x2):w1, w2, theta = 0.5, 0.5, 0.7  # 初始化参数tmp = x1 * w1 + x2 * w2if tmp <= theta:return 0else:return 1# 或门的实现
def OR(x1, x2):w1, w2, theta = 1, 1, 0  # 初始化参数tmp = x1 * w1 + x2 * w2if tmp <= theta:return 0else:return 1# 与非门的实现
def NAND(x1, x2):w1, w2, theta = -0.5, -0.5, -0.7  # 初始化参数tmp = x1 * w1 + x2 * w2if tmp <= theta:return 0else:return 1# 异或门的实现
def XOR(x1, x2):s1 = OR(x1, x2)s2 = NAND(x1, x2)return AND(s1, s2)
result = XOR(1,1)
print(result)