31.下一个排列

思路:
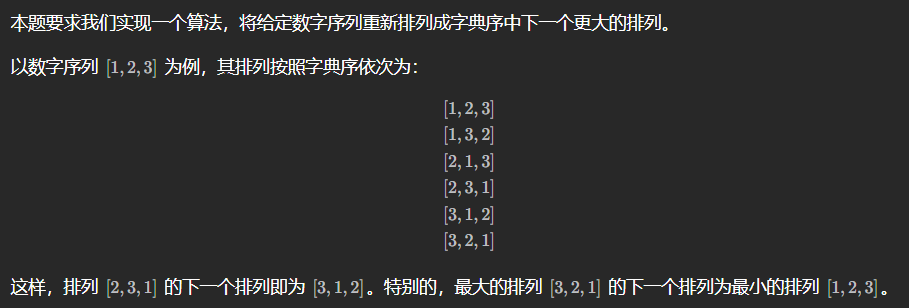
方法:两遍扫描
注意到下一个排列总是比当前排列要大,除非该排列已经是最大的排列。我们希望找到一种方法,能够找到一个大于当前序列的新序列,且变大的幅度尽可能小。具体地:
- 我们需要将一个左边的「较小数」与一个右边的「较大数」交换,以能够让当前排列变大,从而得到下一个排列。
- 同时我们要让这个「较小数」尽量靠右,而「较大数」尽可能小。当交换完成后,「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下,使变大的幅度尽可能小。
以排列 [4,5,2,6,3,1] 为例:
- 我们能找到的符合条件的一对「较小数」与「较大数」的组合为 222 与 3,满足「较小数」尽量靠右,而「较大数」尽可能小。
- 当我们完成交换后排列变为 [4,5,3,6,2,1],此时我们可以重排「较小数」右边的序列,序列变为 [4,5,3,1,2,6]。
具体地,我们这样描述该算法,对于长度为 n的排列 a:
1.首先从后向前查找第一个顺序对 (i,i+1),满足 a[i]<a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。
2.如果找到了顺序对,那么在区间 [i+1,n)中从后向前查找第一个元素 j满足 a[i]<a[j]。这样「较大数」即为 a[j]。
3.交换 a[i] 与 a[j],此时可以证明区间 [i+1,n)必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序,而无需对该区间进行排序。
注意:如果在步骤 1 找不到顺序对,说明当前序列已经是一个降序序列,即最大的序列,我们直接跳过步骤 2 执行步骤 3,即可得到最小的升序序列。
class Solution {public void nextPermutation(int[] nums) {int i = nums.length - 2;while( i>=0 && nums[i] >= nums[i+1]){i--;}if(i >= 0){int j = nums.length - 1;while(j >= 0 && nums[i] >= nums[j]){j--;}swap(nums,i,j);}reverse(nums,i+1); }public void swap(int[] nums,int i ,int j){int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}public void reverse(int[] nums,int start){int left = start,right = nums.length - 1;while(left < right){swap(nums,left,right);left++;right--;}}
}