题目描述：

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

注意：不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

示例 1:

输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"
输出: "56088"

提示：

• 1 <= num1.length, num2.length <= 200
• num1 和 num2 只能由数字组成。
• num1 和 num2 都不包含任何前导零，除了数字0本身。

通过次数

316.8K

提交次数

713.9K

通过率

44.4%

思路和题解：

不能使用任何内置的 BigInteger 库或直接将输入转换为整数，那就只能用数组来模拟数字乘法，也就是小学生的竖式乘法。我们来回忆一下小学生竖式乘法是怎么做的。

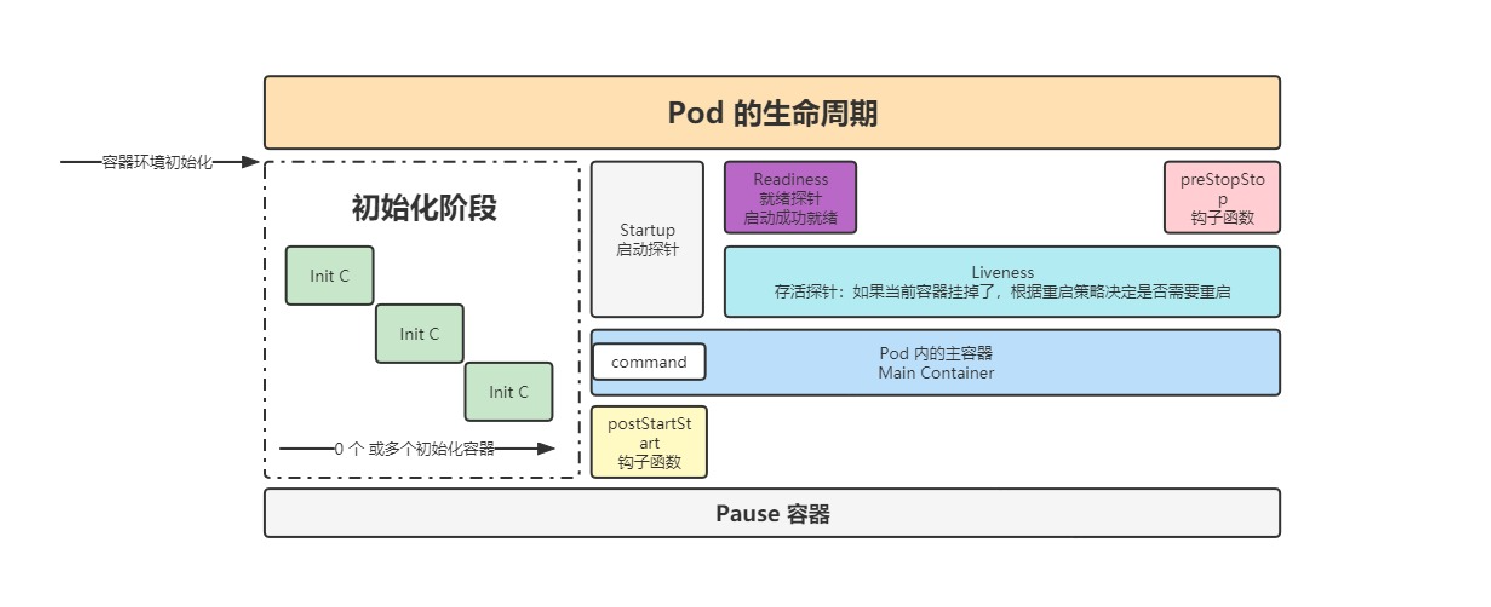
先看第一种，每次两个位数乘完后加上上一次的进位，然后保留余数，记下进位。然后再把乘数a的整体和乘数b每位相乘的结果相加。相加时的进位方式和相乘时一样。直接看图你就懂了。

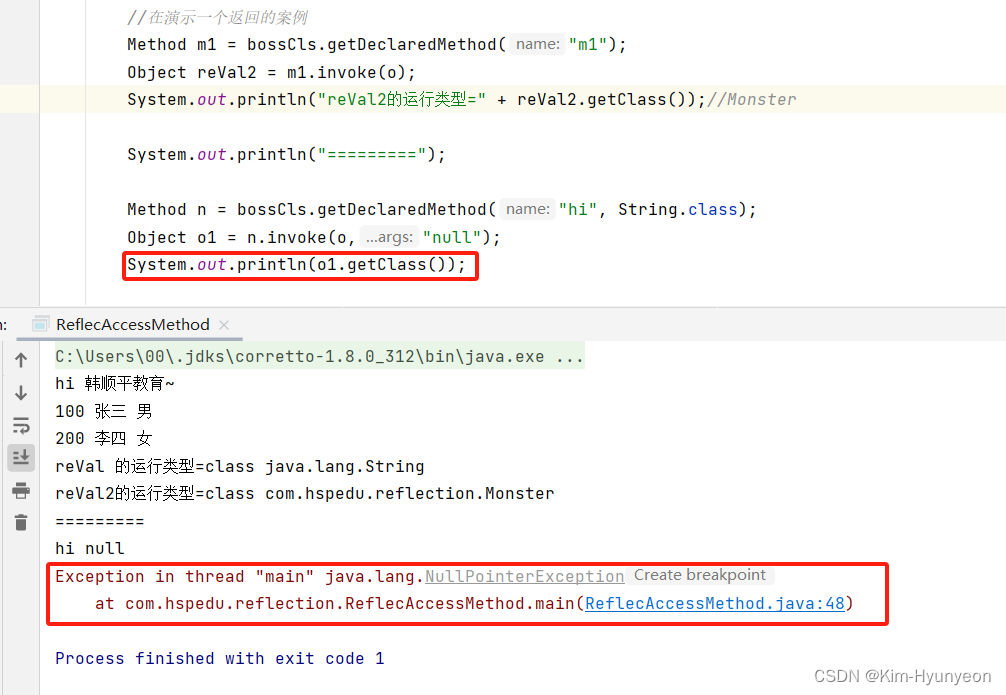
再来看第二种，相乘和相加的时候都不考虑进位，等乘法和加法都做完后再考虑进位，看图你就懂了。

代码：

我用的是第二种方法，先乘法和加法都做完后再搞进位，这样可以不用边乘边加边进位，操作步骤简单些，好写。

class Solution {
public:string multiply(string num1, string num2) {if(num1=="0"||num2=="0")return "0";int m=num1.size(),n=num2.size();string ans;vector<int> ansArr(m+n);int i,j;//相乘for(i=m-1;i>=0;i--){int x=num1[i]-'0';for(j=n-1;j>=0;j--){int y=num2[j]-'0';ansArr[i+j+1]+=x*y;//照理来说是[i+j]，但是[0]的位置要先留着存储最后一个进位，所以向前移一步}}//进位for(i=m+n-1;i>0;i--){ansArr[i-1]+=ansArr[i]/10;ansArr[i]%=10;}//int数组转换为stringi=ansArr[0]==0?1:0;while(i<m+n){ans.push_back(ansArr[i]+'0');//不能用ans[i]=ansArr[i]+'0',这样没用。i++;}return ans;}
};