💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 :阿然成长日记 👈点击可跳转
📆 个人专栏: 🔹数据结构与算法🔹C语言进阶
🚩 不能则学,不知则问,耻于问人,决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍
文章目录
- 一、稳定性的定义:
- 二、排序稳定性的分析:
- (1)冒泡排序
- (2)选择排序
- (3)插入排序
- (4)快速排序
- (5)归并排序
- (6)基数排序
- (7)希尔排序
- (8)堆排序
- 排序算法规律总结:
前言:
前面我们已经学习了八大排序的所有算法,本篇主要讲解每个算法的稳定度推理。
一、稳定性的定义:
例如:一个人的性格很稳定。或是这个人做事的时间很稳定,稳定指的是他做事有着自己固定的速度,而不是越稳定做事越快或越慢。这是我们生活中所理解的稳定。
相同的两个数据排序后,如果相对位置不发生变化,就是稳定的;反之,如果相对位置发生变化,就是不稳定的。
🚩举个例子:
假设小组成员一共A,B,C,D四人,通过一次考试来对他们进行排名。
我们使用一个队列来存储他们的提交顺序:
提交顺序依次是 A,B,C,D
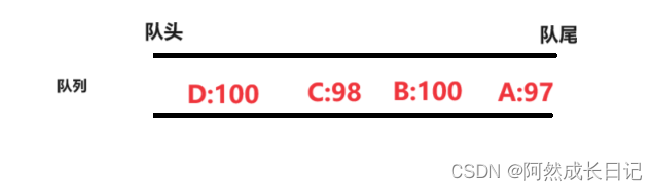
提交完毕,需要对他们进行排序,在这里注意,相同的分数下,通过比较提交的先后次序确定排名。
🔸如果这个排序算法是稳定的,那么排序的次序应该是B,D,C,A; B和D的相对位置先后顺序没有改变。
🔸如果这个排序算法是不稳定的,那么排序的次序应该是D,B,C,A; B和D的相对位置先后顺序改变。
由上可以发现,稳定的算法可以确保排名的准确性。
二、排序稳定性的分析:
(1)冒泡排序
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会执行交换操作的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
(2)选择排序
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n - 1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
(3)插入排序
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。然后是第二个元向前比较,第三个~~;比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
(4)快速排序
以单趟排序是霍尔排序为例,快速排序有两个方向,左边的i下标一直往右走,当a[i] <= a[key],其中key是中枢元素的数组下标,一般取为数组的首元素。而右边的j下标一直往左走,当a[j] > a[key]。如果i和j都走不动了,i <= j,交换a[i]和a[j],重复上面的过程,直到i > j。 交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j] 交换的时刻。
(5)归并排序
归并排序是把一个序列通过递归地分成短序列,直至分到每组只剩一个元素停止,开始并,从只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的一段段的序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也不会i交换,这不会破坏稳定性。那么,在短的有序序列合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序也是稳定的排序算法。
(6)基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以,归并排序也是稳定的排序算法。
(7)希尔排序
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小, 插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比O(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
(8)堆排序
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列,堆排序的过程是从第n / 2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n / 2 - 1, n / 2 - 2, … 1这些个父节点选择元素时,就会破坏稳定性。有可能第n / 2个父节点交换把后面一个元素交换过去了,而第n / 2 - 1个父节点把后面一个相同的元素没 有交换,那么这2个相同的元素之间的稳定性就被破坏了。所以,堆排序不是稳定的排序算法。
📜综上,得出结论:
🔸不是稳定的排序算法: 选择排序、快速排序、希尔排序、堆排序
🔸稳定的排序算法: 冒泡排序、插入排序、归并排序和,基数排序

排序算法规律总结:
快排: 初始顺序影响较大,有序是,性能最差
插入, 冒泡 : 接近有序,性能最好
希尔:希尔是对插入排序的优化,这种优化是在无序的序列中才有明显的效果,如果序列接近有序,反而是插入最优。
堆排,归并,选择对初始顺序不敏感





![2023年中国液晶电视出口现状、品牌格局及行业发展趋势[图]](https://img-blog.csdnimg.cn/img_convert/5ae2e3e8383669f6dda34ca7dac6acc8.png)