1. 什么是 NumPy?

NumPy是一个功能强大的Python库，主要用于对多维数组执行计算。NumPy这个词来源于两个单词-- Numerical和Python。NumPy提供了大量的库函数和操作，可以帮助程序员轻松地进行数值计算。这类数值计算广泛用于以下任务：

• 机器学习模型：在编写机器学习算法时，需要对矩阵进行各种数值计算。例如矩阵乘法、换位、加法等。NumPy提供了一个非常好的库，用于简单(在编写代码方面)和快速(在速度方面)计算。NumPy数组用于存储训练数据和机器学习模型的参数。

• 图像处理和计算机图形学：计算机中的图像表示为多维数字数组。NumPy成为同样情况下最自然的选择。实际上，NumPy提供了一些优秀的库函数来快速处理图像。例如，镜像图像、按特定角度旋转图像等。

• 数学任务：NumPy对于执行各种数学任务非常有用，如数值积分、微分、内插、外推等。因此，当涉及到数学任务时，它形成了一种基于Python的MATLAB的快速替代。

2. NumPy 中的数组

NumPy提供的最重要的数据结构是一个称为NumPy数组的强大对象。NumPy数组是通常的Python数组的扩展。NumPy数组配备了大量的函数和运算符，可以帮助我们快速编写上面讨论过的各种类型计算的高性能代码。

NumPy围绕这些称为数组的事物展开。实际上它被称之为 ndarrays，使用NumPy提供的这些数组，我们就可以以闪电般的速度执行各种有用的操作，如矢量和矩阵、线性代数等数学运算！

矩阵类似于矢量，除了它由行和列组成; 很像一个网格。可以通过给出它所在的行和列来引用矩阵中的值。在NumPy中，我们通过传递一系列序列来制作数组，就像我们之前所做的那样。

2.1. 创建数组

import numpy as np
a = [[1,2],[10,30],[100,200]]
b = np.array(a)
print(b)

	[[  1   2][ 10  30][100 200]]

c = np.zeros((2,3))

	array([[0., 0., 0.],[0., 0., 0.]])

d = np.ones((2,3))

	array([[1., 1., 1.],[1., 1., 1.]])

2.2. 用Numpy的数据

2.2.1. OpenCV

import numpy as np
import cv2img=cv2.imread('img\heart1.JPG')
h,w,l=img.shape

2.2.2. Pandas

import pandas as pddf = pd.DataFrame(b,columns=['a','b'])
print(df)
df.values

	     a    b0    1    21   10   302  100  200array([[  1,   2],[ 10,  30],[100, 200]])

3. 数学计算

3.1. 四则计算

使用四则运算符 +、- 、*、/ 来完成运算操作。乘法运算符执行逐元素乘法而不是矩阵乘法。 要执行矩阵乘法，你可以执行以下操作。

3.1.1. 矩阵乘法

• 概念：矩阵乘法是指两个矩阵进行乘法运算的过程。
• 运算方法：若$A$为$m\times n$的矩阵，$B$为$n\times p$的矩阵，则其乘积$C=A\times B$为$m\times p$的矩阵。其中，$C$的第$i$行、第$j$列元素的计算方法为$C_{i,j}={\sum }_{k=1}^n{A}_{i,k}\times B_{k,j}$。
• 特点：
  • 矩阵乘法不满足交换律，即$A\times B\ne B\times A$。
  • 矩阵乘法满足结合律，即$(A\times B)\times C=A\times (B\times C)$。
  • 矩阵乘法可以用于矩阵的变换。

$A\times B=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\\ A_{31}& A_{32}\end{array}\right]\times \left[\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right]=\left[\begin{array}{cc}{A}_{11}{B}_{11}+A_{12}{B}_{21}& A_{11}{B}_{21}+A_{12}{B}_{22}\\ A_{21}{B}_{11}+A_{22}{B}_{21}& A_{21}{B}_{21}+A_{22}{B}_{22}\\ A_{31}{B}_{11}+A_{32}{B}_{21}& A_{31}{B}_{21}+A_{32}{B}_{22}\end{array}\right]$

numpy的dot()函数称为点积。

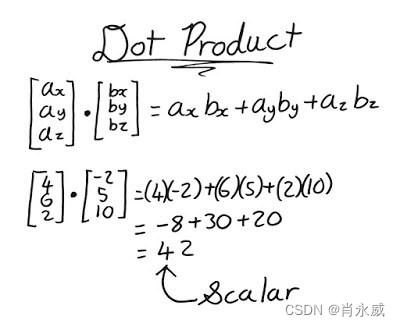
3.1.2. 点乘

• 概念：点乘是指两个向量逐一对应的元素相乘，并将结果相加的过程。
• 运算方法：若$A=(a_1,a_2,a_3,\dots ,a_n)$，$B=(b_1,b_2,b_3,\dots ,b_n)$为两个$n$维向量，则其点乘$C=A\cdot B$为一个标量，其计算方法为$C={\sum }_{i=1}^n{a}_i\times b_i$。
• 特点：
  • 点乘满足交换律，即$A\cdot B=B\cdot A$。
  • 点乘也称为内积，可以用于计算向量的模长和向量之间的夹角。
  • 点乘也可以用于计算两个向量之间的相似度。

$A\times B=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\times \left[\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right]=\left[\begin{array}{cc}{A}_{11}{B}_{11}& A_{12}{B}_{12}\\ A_{21}{B}_{21}& A_{22}{B}_{22}\end{array}\right]$

例如：

import numpy as npa = np.array([[1,2],[4,5]])
b = np.array([[1,2],[3,4]])
c = np.dot(a,b)       # 矩阵乘法，点积
d = np.multiply(a,b)  # 矩阵叉乘，点乘
e = a@b
f = a*b
print('c=e',c)
print('d=f',d)

	c=e [[ 7 10][19 28]]d=f [[ 1  4][12 20]]

3.2. 求逆矩阵与伪逆矩阵

逆矩阵概念：设$A$是一个n阶矩阵，若存在另一个n阶矩阵$B$，使得：$AB=BA=E$ ，则称方阵$A$可逆，并称方阵$B$是$A$的逆矩阵，不是所有的矩阵都存在逆矩阵的，但有时候不得不用到，举个例子：

$AX=B$，则：$X=A^{-1}B$

当$A$可逆的时候完全没问题，但是当$A$不可逆的时候只能用pinv求伪逆矩阵，照样能得到结果，但是存在一定的误差，不能忽略。

import numpy as npa = np.array([[1, 0, 0],[0, 6, 0],[0, 0, 9]])
print('\n', np.linalg.inv(a))  # 求逆矩阵
print('\n', np.linalg.pinv(a))  # 求伪逆矩阵，当本身就可逆的时候，二者结果相同b = np.array([[1, 4, 1, 5]])
print('\n', np.linalg.pinv(b))
print('\n', b @ np.linalg.pinv(b))  # 可以看到伪逆矩阵的性质还是使它们俩相乘为E

	 [[1.         0.         0.        ][0.         0.16666667 0.        ][0.         0.         0.11111111]][[1.         0.         0.        ][0.         0.16666667 0.        ][0.         0.         0.11111111]][[0.02325581][0.09302326][0.02325581][0.11627907]][[1.]]

3.3. 判断矩阵相等

numpy中的allclose函数用于比较两个数组是否相等。

例如逆矩阵运算，判断是否相等。

import numpy as npa = np.array([[1., 2.], [3., 4.]])
ainv = np.linalg.inv(a)
np.allclose(np.dot(a, ainv), np.eye(2))

	True

正常情况下，np.allclose会按照元素在数组中的顺序依次进行比较。例如：

import numpy as np
a = np.array([1, 2, 3])
b = np.array([1, 2, 3])
c = np.array([3, 2, 1])
print(np.allclose(a, b)) # True
print(np.allclose(a, c)) # False

3.4. np.eye()函数生成对角阵

函数的原型：numpy.eye(N,M=None,k=0,dtype=<class ‘float’>,order='C)

返回的是一个二维2的数组(N,M)，对角线的地方为1，其余的地方为0.

参数介绍：

• N:int型，表示的是输出的行数
• M：int型，可选项，输出的列数，如果没有就默认为N
• k：int型，可选项，对角线的下标，默认为0表示的是主对角线，负数表示的是低对角，正数表示的是高对角。
• dtype：数据的类型，可选项，返回的数据的数据类型
• order：{‘C’，‘F’}，可选项，也就是输出的数组的形式是按照C语言的行优先’C’，还是按照Fortran形式的列优先‘F’存储在内存中

import numpy as npa=np.eye(3)
print(a)a=np.eye(4,k=1)
print(a)

	[[1. 0. 0.][0. 1. 0.][0. 0. 1.]][[0. 1. 0. 0.][0. 0. 1. 0.][0. 0. 0. 1.][0. 0. 0. 0.]]

深度学习中的高级用法，将数组转成one-hot形式。

import numpy as nplabels=np.array([[1],[2],[0],[1]])
print("labels的大小：",labels.shape,"\n")#因为我们的类别是从0-2，所以这里是3个类
a=np.eye(3)[2]
print("如果对应的类别号是2，那么转成one-hot的形式",a,"\n")res=np.eye(3)[labels.reshape(-1)]
print("labels转成one-hot形式的结果：\n",res,"\n")

	labels的大小： (4, 1) 如果对应的类别号是2，那么转成one-hot的形式 [0. 0. 1.] labels转成one-hot形式的结果：[[0. 1. 0.][0. 0. 1.][1. 0. 0.][0. 1. 0.]] 

4. 统计

4.1. 最大值、最小值、均值+条件

Numpy的min()函数语法如下：

numpy.min(a, axis=None, out=None, keepdims=, initial=, where=)
其中：

• a：数组。
• axis：沿着哪个轴计算最小值，默认为None，表示对整个数组求最小值。
• out：输出数组，用于存储计算结果。
• keepdims：是否保持数组的维度，默认为False，即降维处理。
• initial：初始值，表示在数组中没有元素时的返回值。
• where：条件，只有条件为True的元素才参与计算。

例如：二维数组的最小值
接着，我们来看一个二维数组，求出数组的最小值。

import numpy as npa = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
min_value = np.min(a, axis=1)print(min_value)

输出结果为：[1 4 7]

在这个例子中，我们传递了axis=1参数，表示我们要沿着第二个轴（也就是每一行）求最小值。最终输出的结果是每一行的最小值，形成一个一维数组。注意，这个结果是通过降维得到的。

4.2. numpy.ptp()最大值与最小值的差

numpy.ptp() 函数计算数组中元素最大值与最小值的差（最大值 - 最小值）。

numpy.ptp(a, axis=None, out=None, keepdims=, initial=, where=)
参数说明：

• a: 输入的数组，可以是一个 NumPy 数组或类似数组的对象。
• axis: 可选参数，用于指定在哪个轴上计算峰-峰值。如果不提供此参数，则返回整个数组的峰-峰值。可以是一个整数表示轴的索引，也可以是一个元组表示多个轴。
• out: 可选参数，用于指定结果的存储位置。
• keepdims: 可选参数，如果为 True，将保持结果数组的维度数目与输入数组相同。如果为 False（默认值），则会去除计算后维度为1的轴。
• initial: 可选参数，用于指定一个初始值，然后在数组的元素上计算峰-峰值。
• where: 可选参数，一个布尔数组，用于指定仅考虑满足条件的元素。

import numpy as np a = np.array([[3,7,5],[8,4,3],[2,4,9]])  
print ('我们的数组是：')
print (a)
print ('调用 ptp() 函数：')
print (np.ptp(a))
print ('沿轴 1 调用 ptp() 函数：')
print (np.ptp(a, axis =  1))
print ('沿轴 0 调用 ptp() 函数：')
print (np.ptp(a, axis =  0))

	我们的数组是：[[3 7 5][8 4 3][2 4 9]]			调用 ptp() 函数：7		沿轴 1 调用 ptp() 函数：[4 5 7]		沿轴 0 调用 ptp() 函数：[6 3 6]

5. 其他

5.1. 删除空值与布尔屏蔽

布尔屏蔽是一个有用的功能，它允许我们根据我们指定的条件检索数组中的元素。

首先，查找NaN值的位置，可以使用函数np.isnan()查找NaN值的位置。接着移除NaN值，使用函数np.delete()删除NaN值所在的索引位置。

import numpy as np a = np.array([[3,np.nan,5],[8,4,np.nan],[2,4,9]])  
a

	array([[ 3., nan,  5.],[ 8.,  4., nan],[ 2.,  4.,  9.]])

mask = np.isnan(a)
print(mask)# 使用布尔索引数组来选择非空值的行
non_empty_rows = np.logical_not(np.any(mask, axis=1))
#a = np.delete(a, np.where(mask))
print(non_empty_rows)
# 生成一个不含空值的新数组
cleaned_data = a[non_empty_rows]
print(cleaned_data)

	[[False  True False][False False  True][False False False]][False False  True][[2. 4. 9.]]

其中，np.logical_not这是一个逻辑函数，可按元素计算NOT arr的真值。

5.2. numpy 将uint8转换为int16

例如图像数据，dat.astype(np.int16)。

5.3. 沿轴向连接数组

import numpy as npa = [0 , 1, 2, 3, 4, 5]
# list转numpy数组
a1 = np.array(a)
print(a1)
# 重新调整数据/矩阵为二维
a2 = a1.reshape(3,2)
print(a2)
# 沿着新轴连接数组/矩阵，增加一个维度，形成三维数组/矩阵/向量
a3 = np.stack((a2,a2,a2), axis=2)     
print(a3)
print(a3.shape)# 一维转变为三维
a4 = a1.reshape(3,2,1)
print(a4)

	[0 1 2 3 4 5][[0 1][2 3][4 5]][[[0 0 0][1 1 1]][[2 2 2][3 3 3]][[4 4 4][5 5 5]]](3, 2, 3)

5.4. 如何计算两组数的欧式距离

# Input
a = np.array([1,2,3,4,5])
b = np.array([4,5,6,7,8])# Solution
dist = np.linalg.norm(a-b)
dist
# > 6.7082039324993694

5.5. 如何计算numpy数组的移动平均值

对于给定的一维数组，计算窗口大小为3的移动平均值。

def moving_average(a, n=3) :ret = np.cumsum(a, dtype=float)ret[n:] = ret[n:] - ret[:-n]return ret[n - 1:] / nnp.random.seed(100)
Z = np.random.randint(10, size=10)
print('array: ', Z)
# Method 1
moving_average(Z, n=3).round(2)# Method 2:  # Thanks AlanLRH!
# np.ones(3)/3 gives equal weights. Use np.ones(4)/4 for window size 4.
np.convolve(Z, np.ones(3)/3, mode='valid') # > array:  [8 8 3 7 7 0 4 2 5 2]
# > moving average:  [ 6.33  6.    5.67  4.67  3.67  2.    3.67  3.  ]

参考：

https://www.numpy.org.cn/article/basics/understanding_numpy.html
https://www.numpy.org.cn/article/basics/an_introduction_to_scientific_python_numpy.html
https://www.numpy.org.cn/article/basics/numpy_matrices_vectors.html
https://www.numpy.org.cn/article/advanced/numpy_exercises_for_data_analysis.html
https://www.runoob.com/numpy/numpy-statistical-functions.html
若oo尘. 【Python之numpy库】3.np.linalg.pinv和np.linalg.inv 求逆矩阵与伪逆矩阵. CSDN博客. 2020.11
鸣谦12. 矩阵和向量的点乘与叉乘. CSDN博客. 2021.04