1. 移动零

题目描述

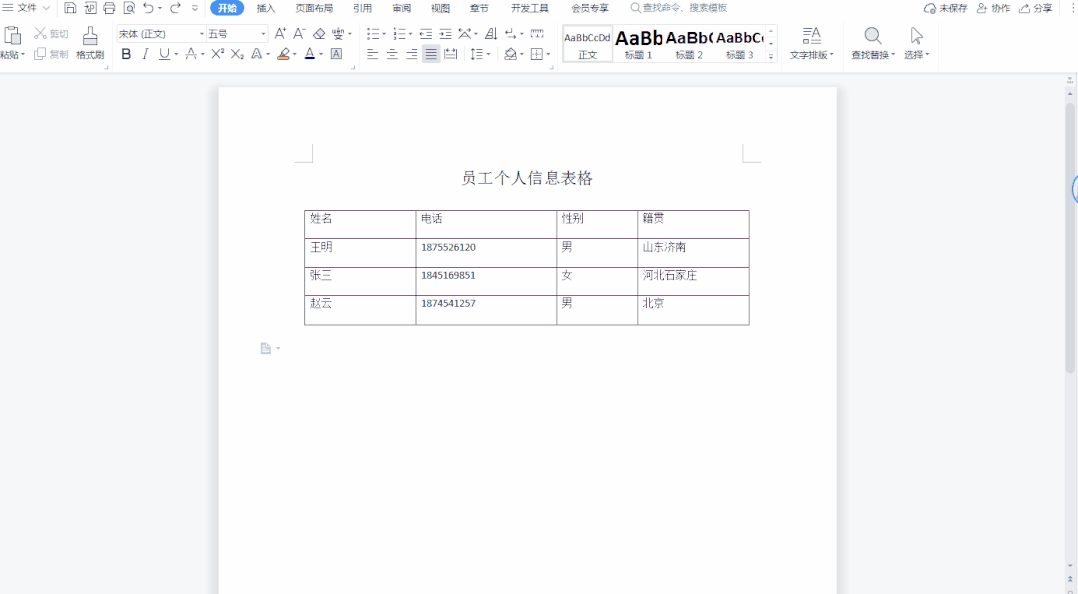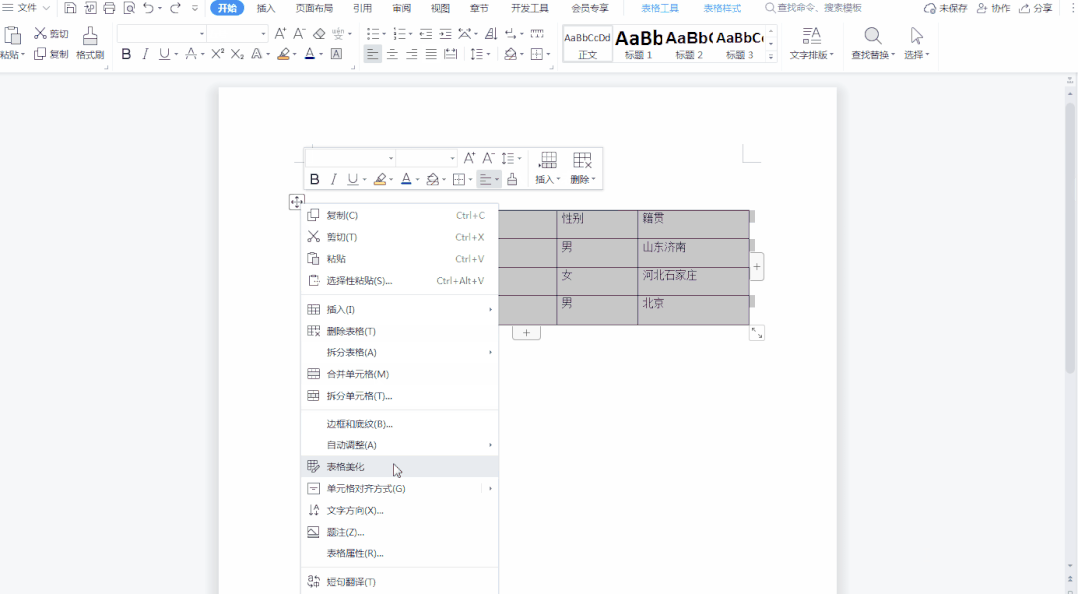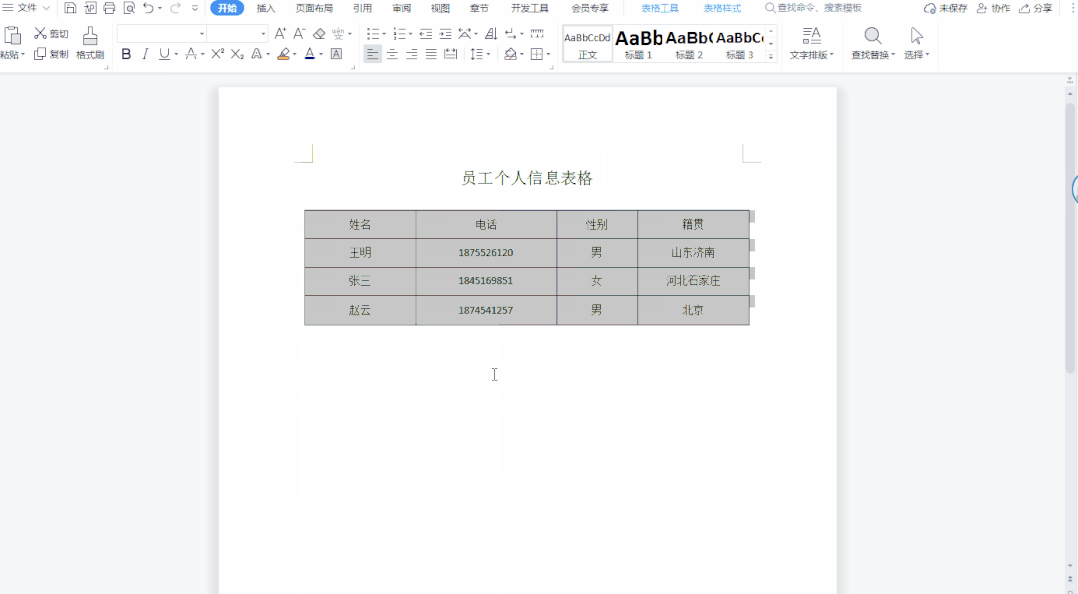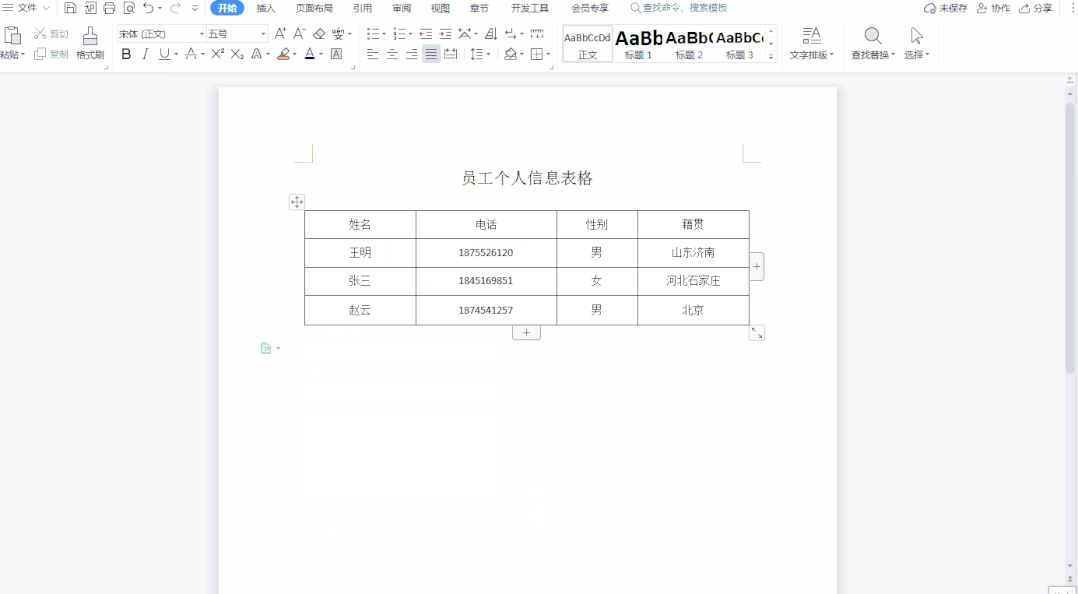
给定一个数组 nums，编写一个方法，将所有零元素移动到数组的末尾，同时保持非零元素的相对顺序不变。必须 原地 修改数组，且不能使用额外的数组。

解题思路

此问题要求将数组中的所有零元素移动到末尾，保持非零元素的相对顺序不变，并且必须在原数组上修改。常规的做法可能会用两个临时数组，但这里需要在 O(1) 空间复杂度下完成任务。因此，我们需要设计一个在原数组上操作的解法。

关键思路：

我们可以使用 双指针法 来解决该问题：

1. 指针 p： 用于遍历数组中的元素，用来指向需要替换的位置（即当前非零元素应该放的位置）。
2. 指针 q： 用于遍历数组中的元素，指向当前正在检查的元素。

步骤：

1. 初始化两个指针 p 和 q：

   • p 指向当前可以插入非零元素的位置。
   • q 用来遍历整个数组，检查每一个元素。

2. 遍历数组：

   • 当 nums[p] 为零时：
     • 如果 nums[q] 也为零，直接跳过 q，继续检查下一个元素。
     • 如果 nums[q] 为非零元素，交换 nums[p] 和 nums[q]，将非零元素移到前面，同时将 p 和 q 向后移动。
   • 当 nums[p] 不是零时，直接将 p 向后移动，继续检查下一个位置。

3. 结束条件： 当 q 遍历完数组时，操作结束。

时间复杂度：

• 单遍历数组，时间复杂度为 O(n)，其中 n 是数组的长度。

空间复杂度：

• 使用了常数空间，仅使用了两个指针，空间复杂度为 O(1)。

代码实现

class Solution {public void moveZeroes(int[] nums) {int p = 0, q = 1;while (q < nums.length) {if (nums[p] == 0) {while (q < nums.length - 1 && nums[q] == 0) {q++;}nums[p] = nums[q];nums[q] = 0;} p++;q++;}}
}

2. 盛最多水的容器

题目解析

题目要求我们在一个给定的整数数组 height[] 中，找到两条垂直线所构成的容器的最大面积。两条线的 x 轴坐标为数组中的两个元素位置，而容器的高度则是由这两个位置的较短的线决定的。

我们可以利用 双指针法 来解决这个问题，这样可以在一次遍历中找到最大面积，且时间复杂度为 O(n)。

解题思路

1. 定义两个指针：

   • 初始化两个指针 p 和 q，分别指向数组的两端。即 p = 0，q = height.length - 1。

2. 计算面积：

   • 在每一步中，我们计算当前两条垂直线之间的面积，面积的计算公式为：
     $\text{area}=(\text{q}-\text{p})\times \min (\text{height[p]},\text{height[q]})$
   • q - p 是两条线之间的宽度，min(height[p], height[q]) 是这两条线所能组成的容器的高度。

3. 移动指针：

   • 为了找到可能的最大面积，我们需要移动其中较短的线来尝试提高容器的高度。我们移动短板的指针，若 height[p] < height[q]，则 p++；否则，q--。通过这种方式，我们不断调整指针，寻找可能的最大面积。

4. 结束条件：

   • 当 p 与 q 相遇时，所有可能的组合都已经检查过，我们返回最大面积。

5. 为什么移动短板

   • 面积是由短板来决定的，如果选择移动长板保留短板，那么移动后的面积不可能比移动前的更大了。 假设移动长板后得到的新板长度比之前的短板长，那么容器的高度仍然是短板的长度，而宽度减小了；如果移动长板后得到的新板长度比之前的短板短，那么面积就更小了。

代码实现

class Solution {public int maxArea(int[] height) {int p = 0, q = height.length - 1;  // 初始化指针int result = 0;  // 用来存储最大面积while (p < q) {int area = (q - p) * Math.min(height[p], height[q]);  // 计算当前的面积result = Math.max(result, area);  // 更新最大面积// 移动短板if (height[p] < height[q]) {p++;  // 如果左边的高度小，移动左指针} else {q--;  // 如果右边的高度小，移动右指针}}return result;  // 返回最大面积}
}

3. 三数之和

问题描述：

给定一个整数数组 nums，找出所有和为零的三元组，要求不重复地返回结果。

解题思路：

这个问题要求在数组中找到所有和为零的三元组，并且不允许返回重复的三元组。考虑到以下几点：

1. 排序：首先，我们可以将数组 nums 进行排序，这样可以更方便地处理重复元素并使用双指针方法进行优化。
2. 去重：由于数组可能包含重复的元素，我们需要跳过重复的三元组。可以通过跳过相同的元素来避免重复结果。
3. 双指针：对于每个固定的 i，我们使用双指针 j 和 k 来遍历剩余的数组，寻找和为零的元素。这样可以有效地减少时间复杂度。
4. 优化：通过判断最小的三个数和最大的两个数的和的情况，提前排除无解的情况，减少不必要的计算。

算法步骤：

1. 排序数组：对 nums 数组进行排序。
2. 遍历数组：用一个 i 来遍历数组，确保 nums[i] 是固定的。
3. 使用双指针：对于每一个固定的 i，使用两个指针 j 和 k 来遍历数组中的元素，查找 nums[i] + nums[j] + nums[k] == 0 的三元组。
4. 跳过重复元素：跳过重复的元素，以避免返回重复的三元组。
5. 优化判断：通过判断数组中最小和最大的元素的和来减少不必要的计算。

代码实现：

class Solution {public List<List<Integer>> threeSum(int[] nums) {// 先把数组变成有序的数组Arrays.sort(nums);List<List<Integer>> ans = new ArrayList<>();int n = nums.length;// 最后留两个位置给 j 和 kfor (int i = 0; i < n - 2; i++) {if (i > 0 && nums[i] == nums[i - 1]) {// 如果和上一个数值相同就跳过，避免重复continue;}int j = i + 1;int k = n - 1;// 优化 1: 最小的三个数加和 > 0 就说明没有 j, k 加一起能 = 0，都 > 0if (nums[i] + nums[i + 1] + nums[i + 2] > 0) break;// 优化 2：nums[i] 和两个最大的数相加都 < 0，说明当前 i 和后面的任意 j, k 相加都 < 0if (nums[i] + nums[n - 1] + nums[n - 2] < 0) continue;while (j < k) {int s = nums[i] + nums[j] + nums[k];if (s == 0) {List<Integer> list = new ArrayList<>();list.add(nums[i]);list.add(nums[j]);list.add(nums[k]);ans.add(list);j++;// 避免重复while (j < k && nums[j] == nums[j - 1]) {j++;}k--;// 避免重复while (k > j && nums[k] == nums[k + 1]) {k--;}} else if (s > 0) {k--;} else {j++;}}}return ans;}
}

4. 接雨水

问题描述：

给定一个整数数组 height，其中每个元素代表一个柱子的高度。请计算能够接住多少个雨水。

解题思路：

此问题是经典的“接雨水”问题。我们需要计算每个位置能接住的雨水量。对于每个位置，能接住的雨水量取决于该位置的左边和右边的最大高度。因此，我们可以将问题转化为以下步骤：

1. 计算每个位置的左边最大高度：对于数组中的每个位置 i，我们可以记录从左到右遍历时，当前位置左边的最大高度。这样可以确定该位置上方能够容纳多少水。
2. 计算每个位置的右边最大高度：对于数组中的每个位置 i，我们可以记录从右到左遍历时，当前位置右边的最大高度。同样，这也帮助我们计算该位置上方能容纳多少水。
3. 计算每个位置的水量：每个位置的水量由当前高度、左边最大高度和右边最大高度共同决定。具体来说，当前位置能容纳的水量为：Math.min(left_max, right_max) - height[i]。

算法步骤：

1. 创建两个数组 pre_max 和 suf_max：分别记录每个位置的左边最大高度和右边最大高度。
2. 计算左边最大高度：从左到右遍历，更新 pre_max[i] 为当前位置 i 及其左边所有位置的最大高度。
3. 计算右边最大高度：从右到左遍历，更新 suf_max[i] 为当前位置 i 及其右边所有位置的最大高度。
4. 计算接住的雨水：对于每个位置 i，水量为 Math.min(pre_max[i], suf_max[i]) - height[i]，然后将水量累加得到总水量。

代码实现：

class Solution {public int trap(int[] height) {int ans = 0;int n = height.length;int[] pre_max = new int[n];int[] suf_max = new int[n];// 计算左边最大高度pre_max[0] = height[0];for (int i = 1; i < n; i++) {pre_max[i] = Math.max(pre_max[i-1], height[i]);}// 计算右边最大高度suf_max[n-1] = height[n-1];for (int i = n-2; i >= 0; i--) {suf_max[i] = Math.max(suf_max[i+1], height[i]);}// 计算每个位置的水量for (int i = 0; i < n; i++) {ans += Math.min(pre_max[i], suf_max[i]) - height[i];}return ans;}
}