SVM支持向量机

定义

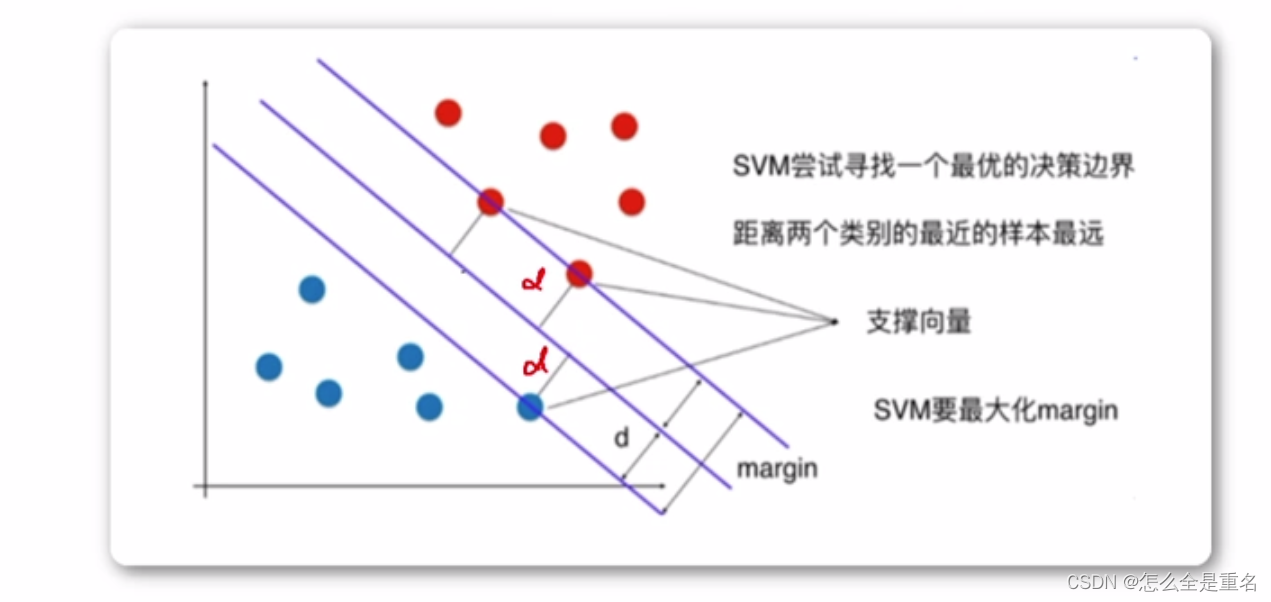
支持向量机（SVM），Supported Vector Machine,基于线性划分，输出一个最优化的分隔超平面，该超平面不但能将两类正确分开,且使分类间隔(margin)最大

**所有训练数据点距离最优分类超平面的距离都要大于支持向量距离此分类超平面的距离
支持向量点到最优分类超平面距离越大越好（margin越大越好）**
SVM的终极目标是求出一个最优的线性分类超平面

SVM的核函数

当在低维空间中，不能对样本线性可分时，将低维空间中的点映射到高维空间中，使它们成为线性可分的，再使用线性划分的原理来判断分类边界。
如果直接采用这种技术在高维空间进行分类或回归，可能在高维特征空间运算时出现"维数灾难"！采用核函数技术(kernel trick)可以有效地解决这样的问题
直接在低维空间用核函数，其本质是用低维空间中的更复杂的运算代替高维空间中的普通内积。
常用的核函数

linear：线性核函数
当训练数据线性可分时，一般用线性核函数，直接实现可分
poly：多项式核函数
rbf：径向基核函数/高斯核函数（Radial Basis Function Kernel）

SVM的"硬间隔"与"软间隔"

硬间隔

当支持向量机（SVM）要求所有样本都必须划分正确，这称为“硬间隔”（hard margin）。
d 表示离超平面最近的样本 x (支持向量) 到超平面的垂直距离

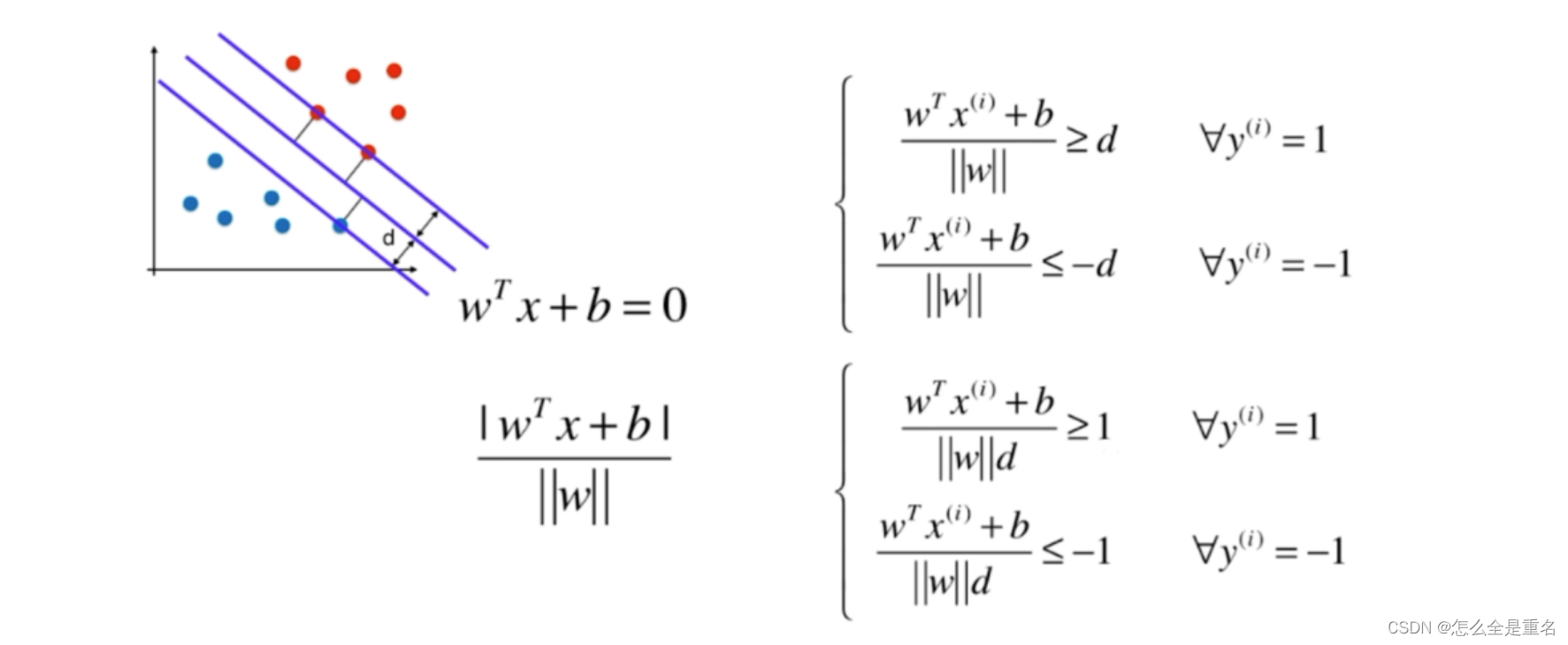
因为分母为常数，所以可将其融入权重 w 与 b 中，不等式中的等号当且仅当x为支持向量时成立

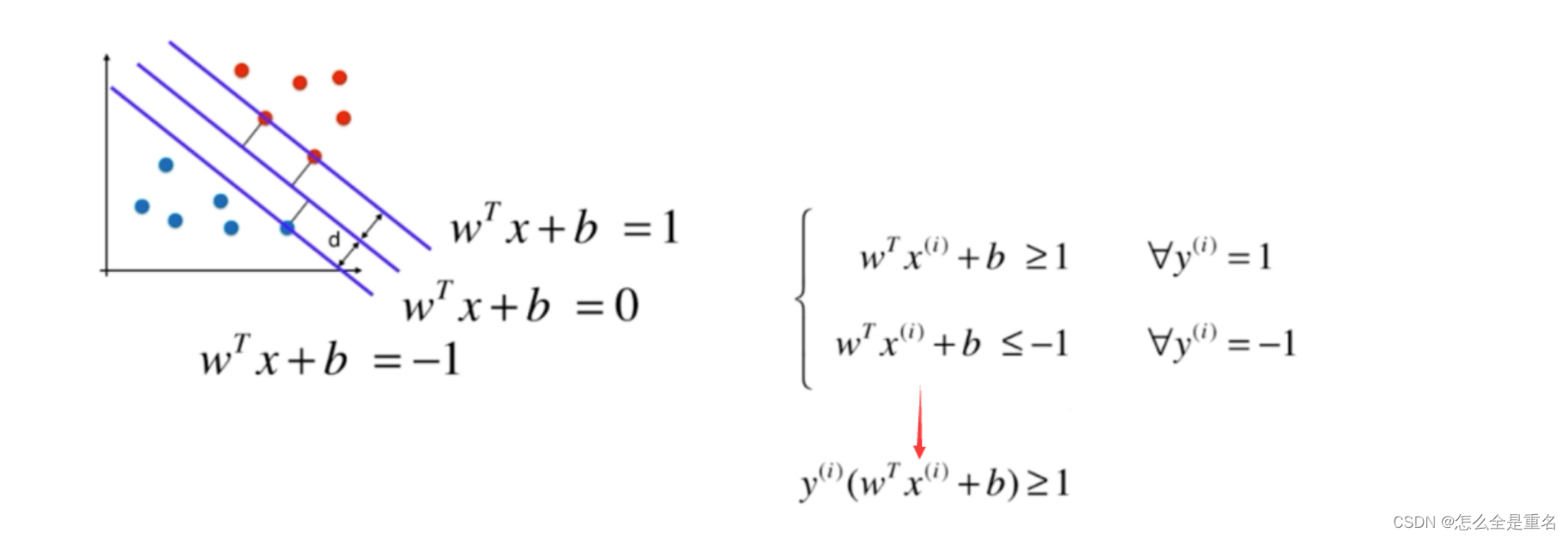
因为y=±1----->wtx+b=1

软间隔

到目前为止，我们一直假定存在一个超平面能将不同类的样本完全划分开。然而，在现实任务中往往很难确定合适的核函数使得训练样本线性可分（即使找到了，也很有可能是在训练样本上由于过拟合所造成的）
缓解该问题的一个办法是允许支持向量机在一些样本上出错，这称为"软间隔"（soft margin）。

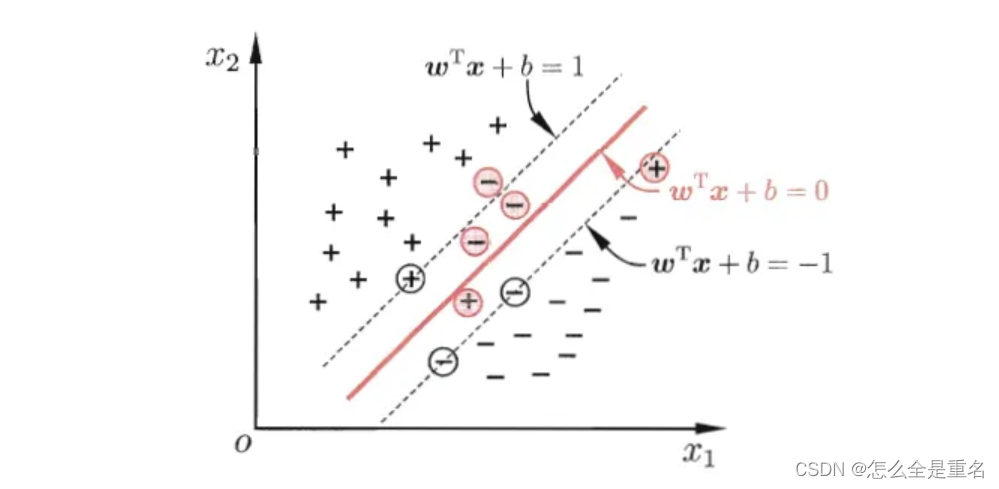
正则项前面的常数C，C越大说明相应的容错空间越小，若C取正无穷，则"逼迫"着每个ζ（也称为“松弛变量”）都必须等于0，此时的Soft Margin SVM就变成了Hard Margin SVM.

简单代码实例

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.metrics import accuracy_score# 加载示例数据集（鸢尾花数据集）
data = datasets.load_iris()
X = data.data  # 特征
y = data.target  # 目标# 只选择两个类别进行二元分类
X = X[y != 0]
y = y[y != 0]# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建支持向量机 (SVM) 分类器
clf = svm.SVC(kernel='linear')	# 核函数选择linear# 训练分类器
clf.fit(X_train, y_train)# 使用分类器进行预测
y_pred = clf.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率:", accuracy)