目录

题目：

示例：

分析：

代码：

---

题目：

示例：

分析：

题目比较简洁,给我们一个元素各不相同的数组，要我们找出该数组里能够组成 a*b=c*d 的组合数目。

比较直观的做法是我们直接暴力枚举，不过这肯定是会超时的，所以我们需要优化一下。

我们把题目换个说法，a*b=c*d 那就是两组乘积相同的数，所以我们就改为一共有多少两组乘积相同的数，得出来的结果需要乘8，因为abcd是可以调换顺序的，就算是同样的4个数，也会产生出8种不同的排列组合。

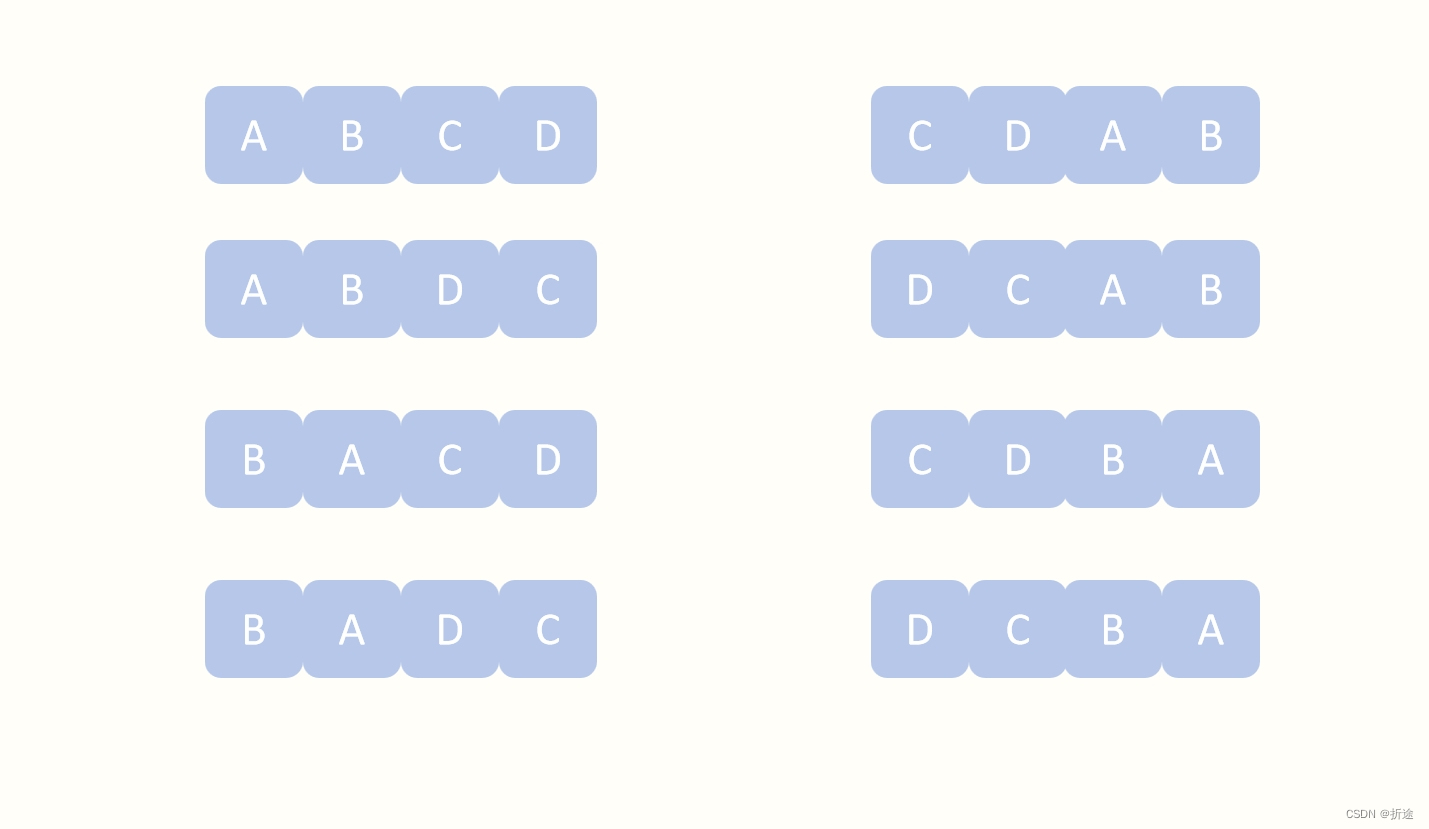
接下来我们就只需要找出数组中有多少两两相乘的乘积相同的数。

题目给的示例中的解释把答案的元组全列出来了，有些许的误导，实际上我们并不需要知道符合答案的元组是什么，我们只要求出元组数量即可。

所以我们两层for循环把数组中任意两个数都给乘一边，把每两个数之前的乘积的所有可能都获取到，用一个map来接收，键是乘积，值是乘积出现的次数。

获取完毕之后我们就得到了所有可能出现的乘积以及能够凑成乘积的元素组数。任意两个组都可以凑成一个a*b=c*d，并且根据我们之前的分析，每凑成一个我们都能得到8种答案。

我们初中应该都学过排列组合，假设能凑成乘积为i的一共有n个组，那么这n个组两两配对，一共会有这么多种可能。

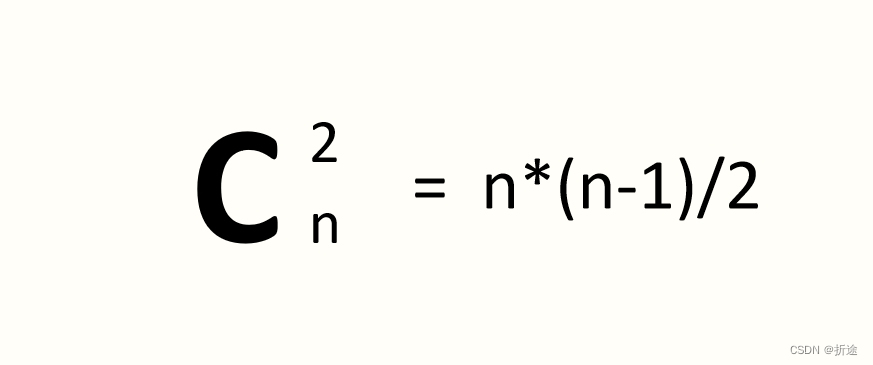
因此把map遍历一边，套这个公式就等得出有多少两组数乘积相同的数量了，最后把这个结果再乘8即可。

代码：

class Solution {
public:int tupleSameProduct(vector<int>& nums) {unordered_map<int,int>m;for(int i=0;i<nums.size();++i){for(int j=i+1;j<nums.size();++j){//获取任意两个元素的乘积数m[nums[i]*nums[j]]++;}}int res=0;for(auto& p:m){//从n里面选出2的排列组合总数res+=(p.second*(p.second-1)/2);}return res*8;}
};