一、代码仓库

https://github.com/Chufeng-Jiang/Python-Linear-Algebra-for-Beginner/tree/main

二、矩阵的基本运算

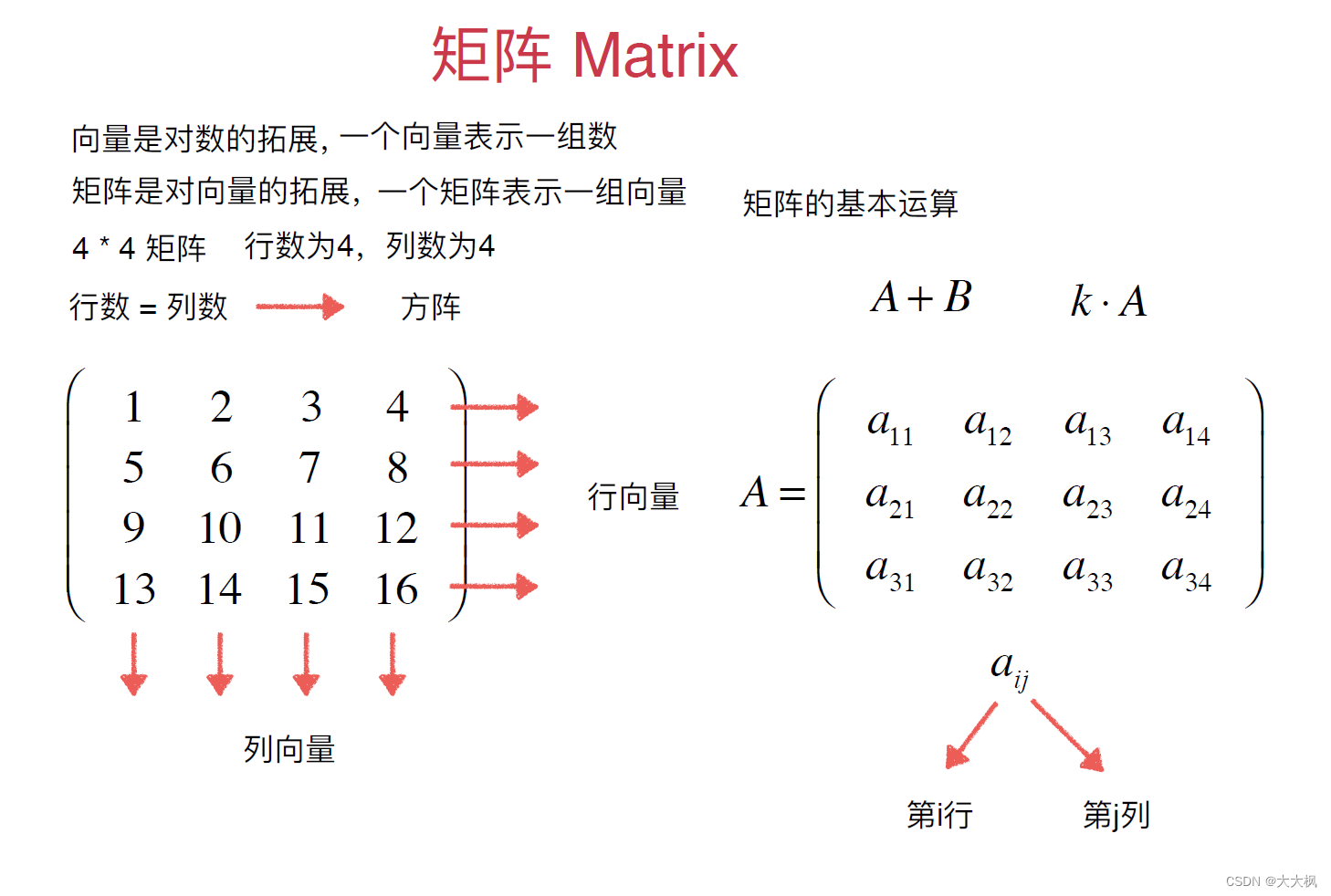
2.1 矩阵的加法

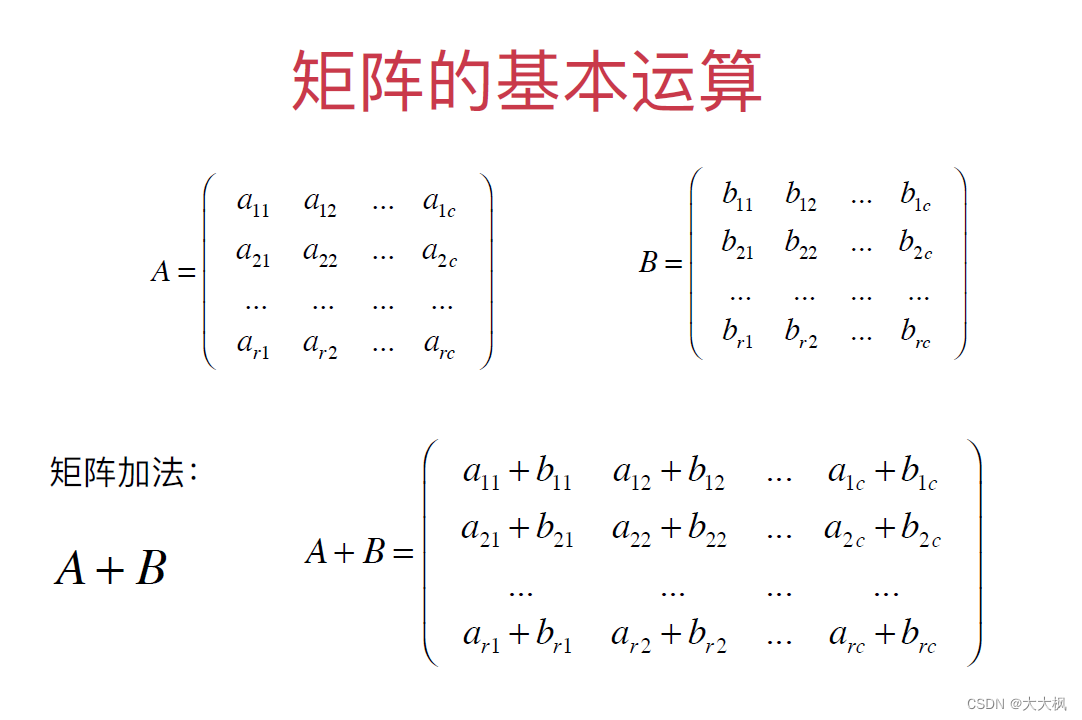
2.2 矩阵的数量乘法

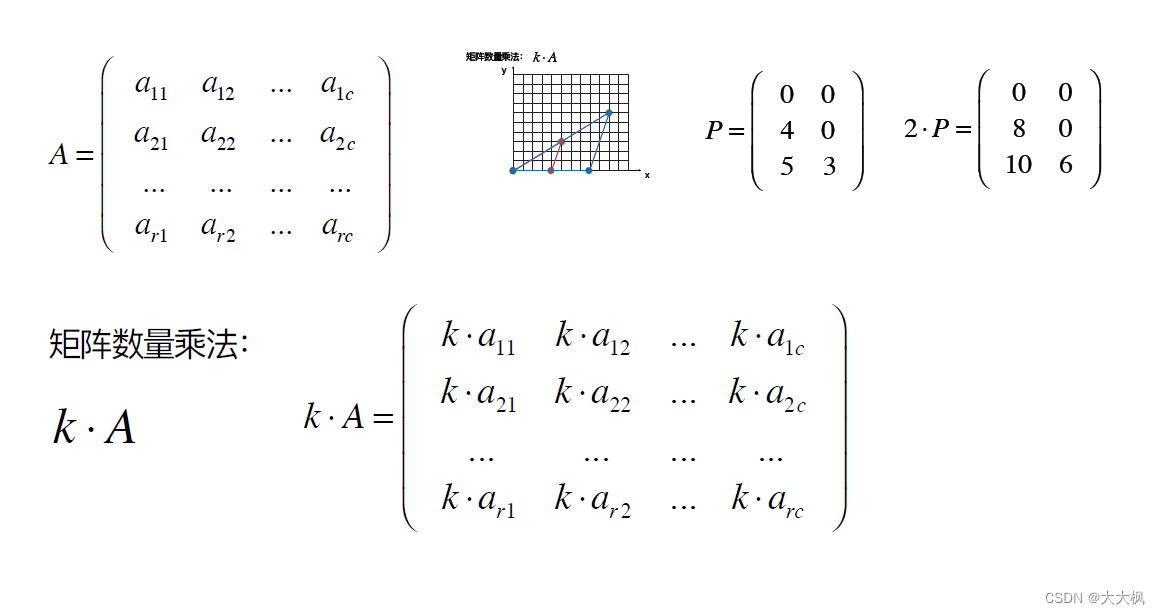
2.3 矩阵和向量的乘法

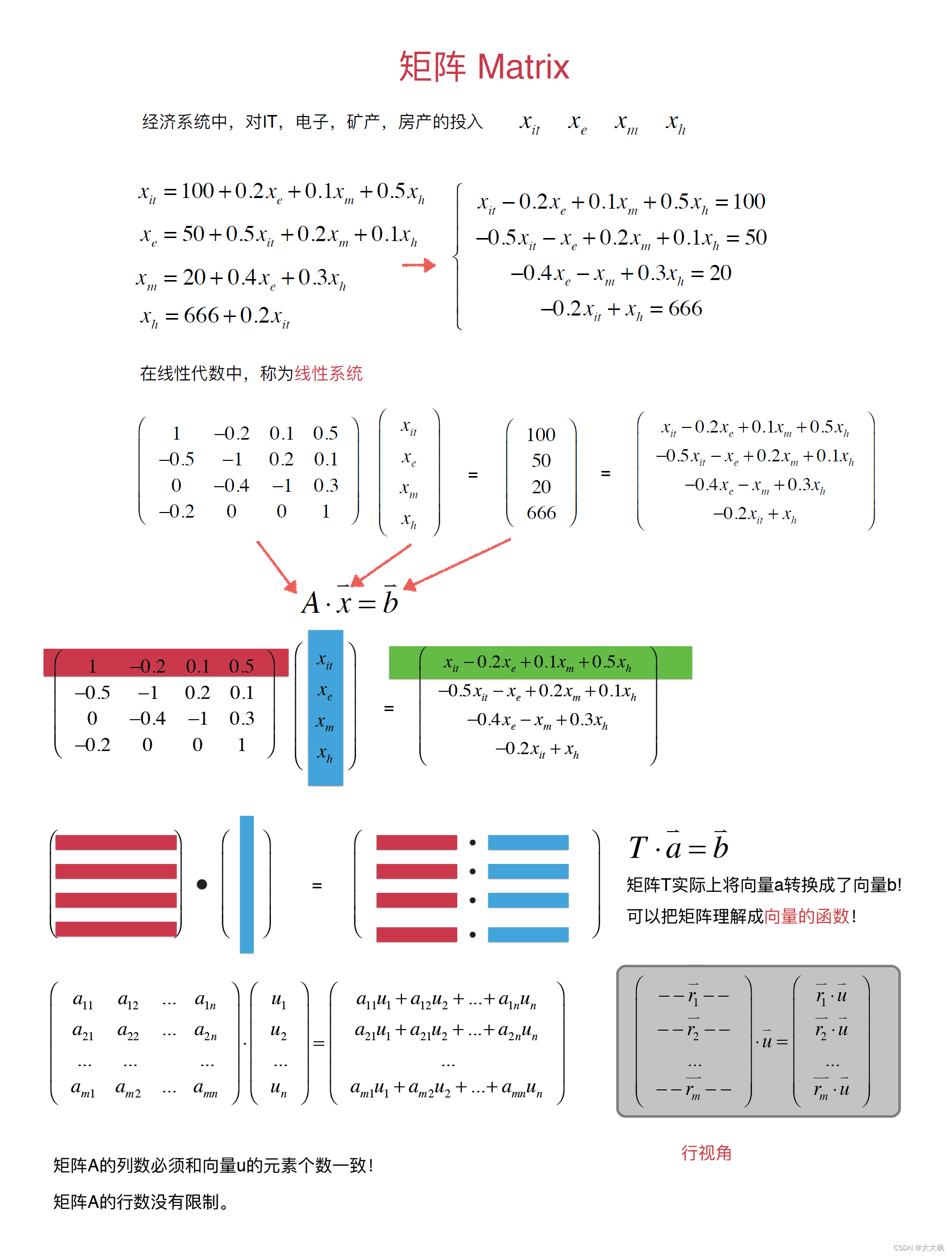
2.4 矩阵和矩阵的乘法

2.5 矩阵的转置

三、手写Matrix代码

Matrix.py

from .Vector import Vectorclass Matrix:"""参数二：是一个二维列表"""def __init__(self, list2d):self._values = [row[:] for row in list2d]@classmethoddef zero(cls, r, c):"""返回一个r行c列的零矩阵"""return cls([[0] * c for _ in range(r)])def T(self):"""返回矩阵的转置矩阵"""return Matrix([[e for e in self.col_vector(i)]for i in range(self.col_num())])def __add__(self, another):"""返回两个矩阵的加法结果"""assert self.shape() == another.shape(), \"Error in adding. Shape of matrix must be same."return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __sub__(self, another):"""返回两个矩阵的减法结果"""assert self.shape() == another.shape(), \"Error in subtracting. Shape of matrix must be same."return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def dot(self, another):"""返回矩阵乘法的结果"""if isinstance(another, Vector):# 矩阵和向量的乘法assert self.col_num() == len(another), \"Error in Matrix-Vector Multiplication."return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])if isinstance(another, Matrix):# 矩阵和矩阵的乘法assert self.col_num() == another.row_num(), \"Error in Matrix-Matrix Multiplication."return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())]for i in range(self.row_num())])def __mul__(self, k):"""返回矩阵的数量乘结果: self * k"""return Matrix([[e * k for e in self.row_vector(i)]for i in range(self.row_num())])def __rmul__(self, k):"""返回矩阵的数量乘结果: k * self"""return self * kdef __truediv__(self, k):"""返回数量除法的结果矩阵：self / k"""return (1 / k) * selfdef __pos__(self):"""返回矩阵取正的结果"""return 1 * selfdef __neg__(self):"""返回矩阵取负的结果"""return -1 * selfdef row_vector(self, index):"""返回矩阵的第index个行向量"""return Vector(self._values[index])def col_vector(self, index):"""返回矩阵的第index个列向量"""return Vector([row[index] for row in self._values])def __getitem__(self, pos):"""返回矩阵pos位置的元素"""r, c = posreturn self._values[r][c]def size(self):"""返回矩阵的元素个数"""r, c = self.shape()return r * cdef row_num(self):"""返回矩阵的行数"""return self.shape()[0]__len__ = row_numdef col_num(self):"""返回矩阵的列数"""return self.shape()[1]def shape(self):"""返回矩阵的形状: (行数， 列数)"""return len(self._values), len(self._values[0])def __repr__(self):return "Matrix({})".format(self._values)__str__ = __repr__

main_matrix.py

from playLA.Vector import Vector
from playLA.Matrix import Matrixif __name__ == "__main__":matrix = Matrix([[1, 2], [3, 4]])print(matrix)print("matrix.shape = {}".format(matrix.shape()))print("matrix.size = {}".format(matrix.size()))print("len(matrix) = {}".format(len(matrix)))print("matrix[0][0] = {}".format(matrix[0, 0]))matrix2 = Matrix([[5, 6], [7, 8]])print(matrix2)print("add: {}".format(matrix + matrix2))print("subtract: {}".format(matrix - matrix2))print("scalar-mul: {}".format(2 * matrix))print("scalar-mul: {}".format(matrix * 2))print("zero_2_3: {}".format(Matrix.zero(2, 3)))T = Matrix([[1.5, 0], [0, 2]])p = Vector([5, 3])print("T.dot(p) = {}".format(T.dot(p)))P = Matrix([[0, 4, 5], [0, 0, 3]])print("T.dot(P) = {}".format(T.dot(P)))print("A.dot(B) = {}".format(matrix.dot(matrix2)))print("B.dot(A) = {}".format(matrix2.dot(matrix)))print("P.T = {}".format(P.T()))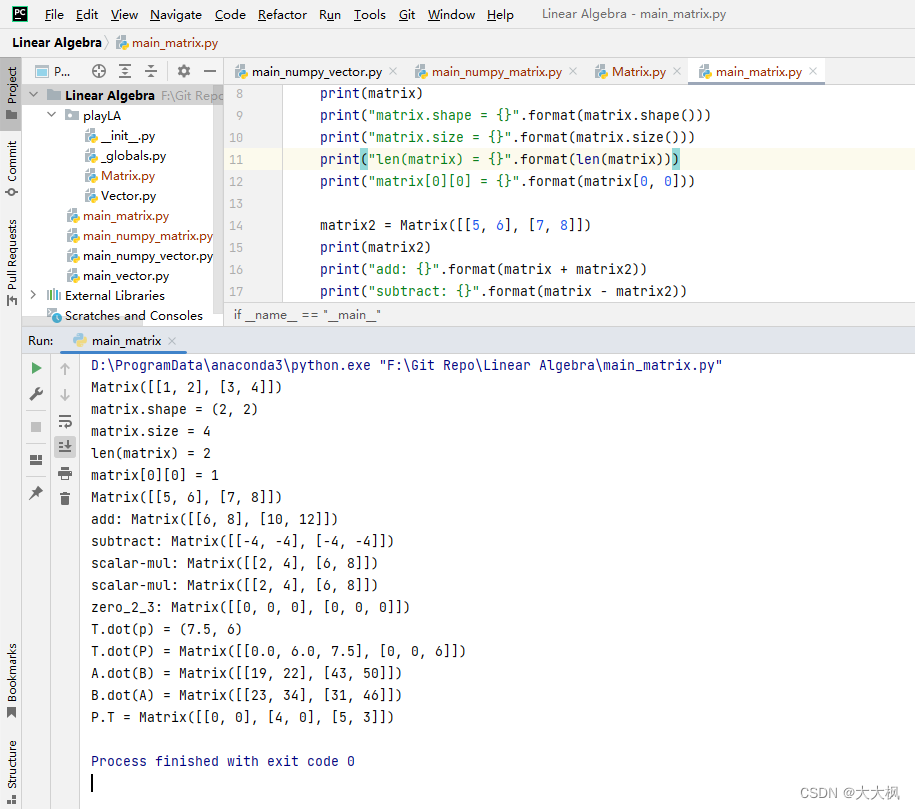

main_numpy_matrix.py

import numpy as npif __name__ == "__main__":# 矩阵的创建A = np.array([[1, 2], [3, 4]])print(A)# 矩阵的属性print(A.shape)print(A.T)# 获取矩阵的元素print(A[1, 1])print(A[0])print(A[:, 0])print(A[1, :])# 矩阵的基本运算B = np.array([[5, 6], [7, 8]])print(A + B)print(A - B)print(10 * A)print(A * 10)print(A * B)print(A.dot(B))p = np.array([10, 100])print(A + p)print(A + 1)print(A.dot(p))