[moeCTF 2023] crypto

这个比赛从8月到10月，漫长又不分段。结束了以后前边的都基本上忘光了。还是分段提交的好点，有机会写写。不过反正也是新生赛，又不是新生只是打个热闹。

ezrot

厨子解决大部分问题

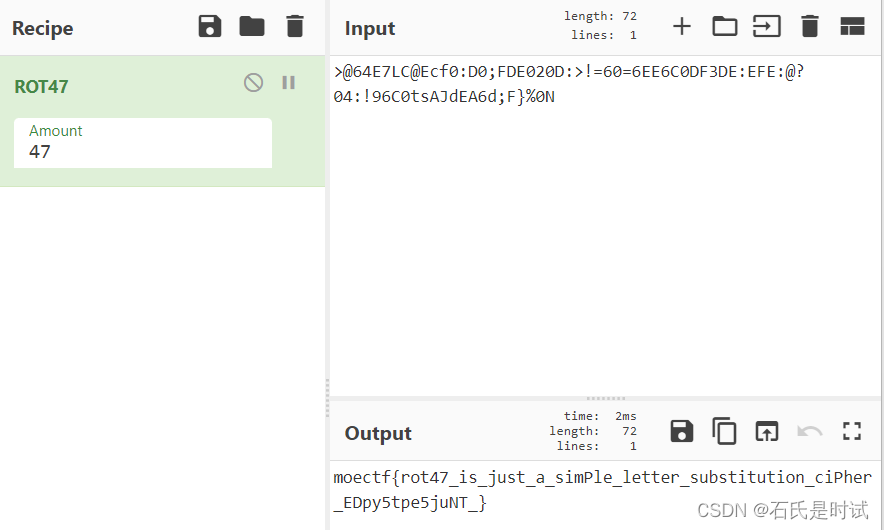
可可的新围墙

给了1个串

mt3_hsTal3yGnM_p3jocfFn3cp3_hFs3c_3TrB__i3_uBro_lcsOp}e{ciri_hT_avn3Fa_j

经过思考发现根据头确定处理的顺序

a = 'mt3_hsTal3yGnM_p3j'
b = 'ocfFn3cp3_hFs3c_3TrB__i3_uBro_lcsOp}'
c = 'e{ciri_hT_avn3Fa_j'flag = ''
for i in range(18):flag += a[0]+b[0]+c[0]+b[1]a = a[1:]b = b[2:]c = c[1:]print(flag)

皇帝的新密码

tvljam{JhLzhL_JPwoLy_Pz_h_cLyF_zPtwPL_JPwoLy!_ZmUVUA40q5KbEQZAK5Ehag4Av}

结构都已经有了，只是这偏移怎么上移法，根据头判断

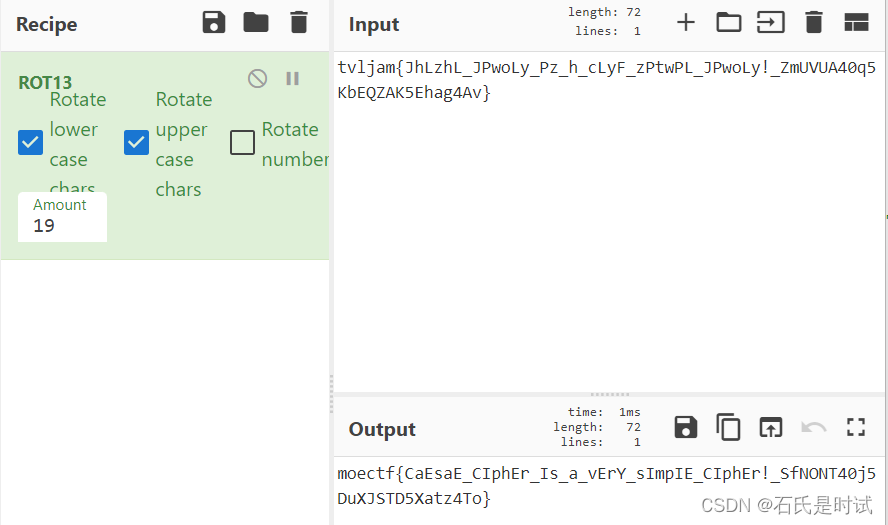
不是“皇帝的新密码”

scsfct{wOuSQNfF_IWdkNf_Jy_o_zLchmK_voumSs_zvoQ_loFyof_FRdiKf_4i4x4NLgDn}

维吉尼亚密码，试出头来就出来了

猫言喵语

喵喵？喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵喵喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵喵喵喵喵喵喵？喵喵喵喵喵？喵喵喵喵喵喵喵喵喵喵喵？喵喵喵喵喵喵喵喵喵喵喵？喵喵喵喵喵喵喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵？喵喵喵喵喵喵喵喵？喵喵？喵喵？喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵喵喵喵喵喵喵？喵喵喵喵喵？喵喵？喵喵喵喵喵喵喵喵？喵喵？喵喵喵喵喵？喵喵喵喵喵？喵喵喵喵喵？喵喵喵喵喵喵喵喵？

有3种符号，明显是用空格来分隔的。经测试喵喵?转成. 喵喵喵转成- 转成摩尔斯码

- .... . ..--.- -.- .- .-- .- .. .. ..--.- -.-. .- - ..--.- -... ..- - ..--.- -... . ..--.- -.-. .- .-.. .-.. . -.. ..--.- --. --- ..- --.. .. ..--.- -... -.-- ..--.- .-. -..-

THE_KAWAII_CAT_BUT_BE_CALLED_GOUZI_BY_RX

baby_e

from Crypto.Util.number import getPrime,bytes_to_longp,q = getPrime(2048),getPrime(2048)
e = 7
n = p*q
m = bytes_to_long(open('flag.txt','rb').read().strip())
c = pow(m,e,n)
print("c = ",c)
print("n = ",n)# c =  147693154873835354725007152781732424355869776162377337823960431913672366269917723916891506269449726723757821517328874729037838600793748824028829185409932536014732765063216715033843955453706710187792772702199448156372644163429786386035008302836467605094954587157232829525150652611067567669525072625329634860065850520051628272535479197120008981979404760445193750864902244921407742155742716289495581989134730376783828846663464819337418977287363028738701414486788851136608957124505485242331701209645216580641917007780811842757125048746184068597664780265422321550909392419865169775282217442331295071069272774722564587602419768461231775480847018941840911357926330143045826277813722919121117172763493242590521245640828462665947672485094793188432098216701511715232654611338293295459889814699850788048985878279440740712956248569068077253790198036918598519191892836075254345518967666166925163908185663991353344555402397055977817370082929420443034626201745027965444069777059760865359310439815816749939498993014457995041394803598825093836045546578310632172636478575946653375857640993393714607308326474003446154152048840071034349831168612740218034679021240949747357214453636633636662650940968576792518622437627529244515229173
# n =  553409369582823237678532685244026647155180191225879439432235077135813123637186465008813830373646133388592395760175777499266561095087891764348044063111935877931069321764391883899483374576303169645488542398590564148654412004383012178107972880058460460806768779452529433458826925606225797078653905380530651390617109384086518728626571028089036812787671647095695947167204428442727185744172445701874820612799168887428075695751162763647868386879374037826876671079326544820609721731078985096813307183878793033824330869698508952853770794414757655681370862323768018291030331209143189638496644361618184164228294031490537429556439588954274708598530042700988138862000054458742762198052079867259365645914383561162796796952346445529346145323567650621600171442575319262718389389870407629339714751583360252884338116164466349449862781112019462555743429653595045695696967783338371470032332852204294900011651434678829104876529439166176589508898757122660322523937330848536715937381297551894198974459004139082562228022412335520195652419375915216074658463954339332593244483927157329404652516225481116614815221154229491846087288087715884363786672244655901308480290011237244562251084095684531716327141154558809471185132979704992609461470501119328696999713829

很明显e很小，而且明显c<n所以可以直接开方

bad_e

from Crypto.Util.number import *
p = getPrime(512)
q = getPrime(512)
e = 65537print(p) # 6853495238262155391975011057929314523706159020478084061020122347902601182448091015650787022962180599741651597328364289413042032923330906135304995252477571
print(q) # 11727544912613560398705401423145382428897876620077115390278679983274961030035884083100580422155496261311510530671232666801444557695190734596546855494472819with open("flag.txt","r") as fs:flag = fs.read().strip()m = bytes_to_long(flag.encode())
c = pow(m,e,p*q)
print(c) # 63388263723813143290256836284084914544524440253054612802424934400854921660916379284754467427040180660945667733359330988361620691457570947823206385692232584893511398038141442606303536260023122774682805630913037113541880875125504376791939861734613177272270414287306054553288162010873808058776206524782351475805

n已经分解好了

flag = long_to_bytes(pow(c,invert(e,(p-1)*(q-1)),p*q))

factor_signin

from Crypto.Util.number import getPrime
from math import prodwith open("flag.txt","rb") as f:flag = f.read().strip()
assert len(flag) == 72m1 = int.from_bytes(flag[:36],"big")
m2 = int.from_bytes(flag[36:],"big")e = 65537p,q = getPrime(2048),getPrime(2048)
n1 = p*q
c1 = pow(m1,e,n1)
print("c1 = ",c1)
print("n1 = ",n1)primes = [getPrime(64) for _ in range(32)]
n2 = prod(primes)
c2 = pow(m2,e,n2)
print("c2 = ",c2)
print("n2 = ",n2)

第1部分，n1可以查到分解，第2部分都是小素数，可以很容易分解

c1 =  10004937130983861141937782436252502991050957330184611684406783226971057978666503675149401388381995491152372622456604317681236160071166819028679754762162125904637599991943368450200313304999566592294442696755822585022667008378021280392976010576970877334159755332946926433635584313137140987588847077645814987268595739733550220882135750267567373532603503399428451548677091911410732474324157868011686641243202218731844256789044721309478991918322850448456919991540932206923861653518190974620161055008847475600980152660468279765607319838003177639654115075183493029803981527882155542925959658123816315099271123470754815045214896642428657264709805029840253303446203030294879166242867850331945166255924821406218090304893024711068773287842075208409312312188560675094244318565148284432361706108491327014254387317744284876018328591380705408407853404828189643214087638328376675071962141118973835178054884474523241911240926274907256651801384433652425740230755811160476356172444327762497910600719286629420662696949923799255603628210458906831175806791599965316549386396788014703044837917283461862338269599464440202019922379625071512100821922879623930069349084917919100015782270736808388388006084027673781004085620817521378823838335749279055639005125
n1 =  343504538870081878757729748260620800783581983635281373321527119223374418103340873199654926888439040391545101913132680017655039577253974802351999985470115474655124168592386965001556620077117966153475518658881140827499124290142523464795351995478153288872749817655925271395693435582010998996210909883510311066017237567799370371513462802547313382594409676803895262837061350017911885033133654781876923251129406855067993830824618637981136966134029212516871210627954762147349788788999116702635535406398258621926040887099782494271000823401788337120154104692934583729065189687995570122890809807661370008740283447636580308161498808092269041815719148127168137018600113465985504975054319601741498799761500526467431533990903047624407330243357514588557352746347337683868781554819821575385685459666842162355673947984514687068626166144076257334426612302554448774082488600083569900006274897032242821388126274957846236552373226099112200392102883351088570736254707966329366625911183721875374731791052229266503696334310835323523568132399330263642353927504971311717117370721838701629885670598853025212521537158141447625623337563164790788106598854822686494249848796441153496412236527242235888308435573209980270776407776277489669763803746640746378181948641
p1 = 18055722101348711626577381571859114850735298658417345663254295930584841136416234624852520581982069555948490061840244710773146585295336094872892685938420880462305333393436098181186277450475949236132458958671804132443554885896037342335902958516394876382378829317303693655605215373555988755516058130500801822723195474873517960624159417903134580987202400855946137101429970119186394052011747475879598126195607938106163892658285305921071673588966184054026228745012993740035399652049777986535759039077634555909031397541116025395236871778797949216479130412500655359057128438928721459688727543057760739527720641179290282309741
q1 = 19024691283015651666032297670418553586155390575928421823630922553034857624430114628839720683172187406577114034710093054198921843669645736474448836706112221787749688565566635453151716934583685087745112614898780150391513798368931496744574075511968933800467288441832780919514199410584786925010518564670786685241724643282580795568609339268652910564215887176803735675069372979560024792322029911970574914829712553975379661212645059271137916107885326625543090473004683836665262304916304580076748336858662108554591235698235221618061328251985929904075811056422186525179189846420226944944513865790999242309352900287977666792901
m1 = long_to_bytes(pow(c1,inverse(e, (p1-1)*(q1-1)),n1))
print(m1)c2 =  4948422459907576438725352912593232312182623872749480015295307088166392790756090961680588458629287353136729331282506869598853654959933189916541367579979613191505226006688017103736659670745715837820780269669982614187726024837483992949073998289744910800139692315475427811724840888983757813069849711652177078415791290894737059610056340691753379065563574279210755232749774749757141836708161854072798697882671844015773796030086898649043727563289757423417931359190238689436180953442515869613672008678717039516723747808793079592658069533269662834322438864456440701995249381880745586708718334052938634931936240736457181295
n2 =  8582505375542551134698364096640878629785534004976071646505285128223700755811329156276289439920192196962008222418309136528180402357612976316670896973298407081310073283979903409463559102445223030866575563539261326076167685019121804961393115251287057504682389257841337573435085535013992761172452417731887700665115563173984357419855481847035192853387338980937451843809282267888616833734087813693242841580644645315837196205981207827105545437201799441352173638172133698491126291396194764373021523547130703629001683366722885529834956411976212381935354905525700646776572036418453784898084635925476199878640087165680193737ps = [
15211380502610462057,
11853704782834170959,
14397830993057803133,
12404642343676224637,
16408421615173973083,
10049235158029375571,
13645878578452317313,
10596280721192026229,
10864078180916418691,
15332916111580607077,
13062839684118954553,
15751974537676958401,
14813953870710226847,
12034779627328165471,
9949603102225364603 ,
17289161209347211817,
16123604149048919099,
14678737767649343977,
17673334943789572513,
11092420583960163379,
18345408081492711641,
14745811312384518031,
10547615587767500213,
16870346804576162551,
17093292308638969889,
18390046459144888243,
18106525049998616747,
15175734709842430433,
14619040595108594017,
17543713628803023199,
12448177342966243757,
17265001711647542137]phi = 1
for v in ps:phi*=v - 1d = inverse(e,phi)
m2 = long_to_bytes(pow(c2,d,n2)) 
#moectf{fACtord6_And_YAfu_Are_6oth_good_utils_to_fACtorize_num6ers_ff90S}

feistel

寻找中。。。。看最后一题吧，是同一个题，一开始作的那个，那个没给key这个给了，比那个简单。

n&n

共模攻击

from Crypto.Util.number import *p = getPrime(1024)
q = getPrime(1024)with open("flag.txt","r") as f:flag = f.read().strip().encode()m = bytes_to_long(flag)
n = p * q
e1 = 0x114514
e2 = 19198101c1 = pow(m,e1,n)
c2 = pow(m,e2,n)
print(c1) 
print(c2)
print(n)c1 =  5776799746376051463605370130675046329799612910435315968508603116759552095183027263116443417343895252766060748671845650457077393391989018107887540639775168897954484319381180406512474784571389477212123123540984850033695748142755414954158933345476509573211496722528388574841686164433315356667366007165419697987147258498693175698918104120849579763098045116744389310549687579302444264316133642674648294049526615350011916160649448726069001139749604430982881450187865197137222762758538645387391379108182515717949428258503254717940765994927802512049427407583200118969062778415073135339774546277230281966880715506688898978925
c2 = 4664955020023583143415931782261983177552050757537222070347847639906354901601382630034645762990079537901659753823666851165175187728532569040809797389706253282757017586285211791297567893874606446000074515260509831946210526182765808878824360460569061258723122198792244018463880052389205906620425625708718545628429086424549277715280217165880900037900983008637302744555649467104208348070638137050458275362152816916837534704113775562356277110844168173111385779258263874552283927767924979691542028126412133709129601685315027689094437957165812994784648540588277901241854031439324974562449032290219652206466731675967045633360
n =13612969130810965900902742090064423006385890357159609755971027204203418808937093492927060428980020085273603754747223030702684866992231913349067578014240319426522039068836171388168087260774376277346092066880984406890296520951318296354893551565670293486797637522297989653182109744864444697818991039473180752980752117041574628063002176339235126861152739066489620021077091941250365101779354009854706729448088217051728432010328667839532327286559570597994183126402340332924370812383312664419874352306052467284992411543921858024469098268800500500651896608097346389396273293747664441553194179933758992070398387066135330851531

e1 = 0x114514
e2 = 19198101
g, x1, x2 = gmpy2.gcdext(e1,e2)   #g!=1, e有公因子需要再开根号
m = pow(c1,x1,n)*pow(c2,x2,n) % n
print(long_to_bytes(int(gmpy2.iroot(m,g)[0])))#moectf{dO_nOt_u53_5AM3_MOdulu5_tO_3ncrYPt_dIFF3r3nt_dAtA!_JY63x33iiA0Ji}

|p-q|

费马分解，p,q距离很近。不过很多软件都会，也可以不必自己用费马分解。

with open("flag.txt","rb") as fs:flag = fs.read().strip()
assert len(flag) == 72m = int.from_bytes(flag,"big")from Crypto.Util.number import getPrime, isPrimedef next_prime(p):while True:p += 2if isPrime(p):return pp = getPrime(2048)
q = next_prime(p)
n = p * q
e = 65537
c = pow(m,e,n)
print("n =",n)
print("c =",c)e = 65537
n = 329960318345010350458589325571454799968957932130539403944044204698872359769449414256378111233592533561892402020955736786563103586897940757198920737583107357264433730515123570697570757034221232010688796344257587359198400915567115397034901247038275403825404094129637119512164953012131445747740645183682571690806238508035172474685818036517880994658466362305677430221344381425792427288500814551334928982040579744048907401043058567486871621293983772331951723963911377839286050368715384227640638031857101612517441295926821712605955984000617738833973829140899288164786111118033301974794123637285172303688427806450817155786233788027512244397952849209700013205803489334055814513866650854230478124920442832221946442593769555237909177172933634236392800414176981780444770542047378630756636857018730168151824307814244094763132088236333995807013617801783919113541391133267230410179444855465611792191833319172887852945902960736744468250550722314565805440432977225703650102517531531476188269635151281661081058374242768608270563131619806585194608795817118466680430500830137335634289617464844004904410907221482919453859885955054140320857757297655475489972268282336250384384926216818756762307686391740965586168590784252524275489515352125321398406426217
c = 307746143297103281117512771170735061509547958991947416701685589829711285274762039205145422734327595082350457374530975854337055433998982493020603245187129916580627539476324521854057990929173492940833073106540441902619425074887573232779899379436737429823569006431370954961865581168635086246592539153824456681688944066925973182272443586463636373955966146029489121226571408532284480270826510961605206483011204059402338926815599691009406841471142048842308786000059979977645988396524814553253493672729395573658564825709547262230219183672493306100392069182994445509803952976016630731417479238769736432223194249245020320183199001774879893442186017555682902409661647546547835345461056900610391514595370600575845979413984555709077635397717741521573798309855584473259503981955303774208127361309229536010653615696850725905168242705387575720694946072789441481191449772933265705810128547553027708513478130258801233619669699177901566688737559102165508239876805822898509541232565766265491283807922473440397456701500524925191214292669986798631732639221198138026031561329502985577205314190565609214349344303324429408234237832110076900414483795318189628198913032900272406887003325858236057373096880675754802725017537119549989304878960436575670784578550

from math import isqrt,is_square
def factorize(N):"""Recovers the prime factors from a modulus using Fermat's factorization method.:param N: the modulus:return: a tuple containing the prime factors, or None if the factors were not found"""a = isqrt(N)b = a * a - Nwhile b < 0 or not is_square(b):a += 1b = a * a - Np = a - isqrt(b)q = N // pif p * q == N:return p, qp,q = factorize(n)>>> from Crypto.Util.number import *
>>> d = invert(e,(p-1)*(q-1))
>>> m = pow(c,d,n)
>>> long_to_bytes(m)
b'moectf{it_iS_vUlnErablE_iF_p_iS_aboUt_thE_SaME_SiZE_aS_Q_MVoAYArrlG3uco}'

rsa_signin

给了一堆n,c这里边有一对有公因子

with open("flag.txt","rb") as f:flag = f.read().strip()m = int.from_bytes(flag, "big")
e = 65537from Crypto.Util.number import getPrimefor x in range(10):p = getPrime(1024)q = getPrime(1024)n = p * qc = pow(m, e, n)print("n =", n)print("c =", c)n1 = 17524722204224696445172535263975543817720644608816706978363749891469511686943372362091928951563219068859089058278944528021615923888948698587206920445508493551162845371086030869059282352535451058203615402089133135136481314666971507135484450966505425514285114192275051972496161810571035753943880190780759479521486741046704043699838021850105638224212696697865987677760179564370167062037563913329993433080123575434871852732981112883423565015771421868680113407260917902892944119552200927337996135278491046562185003012971570532979090484837684759828977460570826320870379601193678304983534424368152743368343335213808684523217
c1 = 6870605439714128574950893771863182370595667973241984289208050776870220326525943524507319708560433091378319367164606150977103661770065561661544375425887970907060665421562712515902428061727268441585629591525591001533188276465911918724808701356962871139957343861919730086334623932624184172272488406793955068827527130338853980609365042071290967556159598511667974987218999253443575482949258292953639729393456515185185102248985930422080581185292420347510600574229080211050520146551505605537486989306457793451086767402197128573781597156939709237045132856159368959981648969874765462190363842275826077556314448408825308218451
n2 = 24974121071274650888046048586598797033399902532613815354986756278905133499432183463847175542164798764762683121930786715931063152122056911933710481566265603626437742951648885379847799327315791800670175616973945640322985175516271373004547752061826574576722667907302681961850865961386200909397231865804894418194711076667760169256682834206788730947602211228930301853348503098156592000286467190760378847541148772869356389938999094673945092387627113807899212568399028514283219850734634544982646070106811651490010946670117927664594365986238107951837041859682547029079035013475238052160645871718246031144694712586073789250183
c2 = 10324627733161143472233272675096997859064721978612320424254305978486200326061730105384511258706433940176741256952824288120499229240005823611541292676234913505775165761543820764046537413943393325463602612485849366939102550336256797820440347815027443410399157963547486098366749815425187247171697678576246606105486928212486117878157055321965270364583625270716186820068538749425299073309429589410882809098930213978117176627031795312102177342499674234163614021182116065492884880492891668658240362567156235958605768725892407536211503981819707919444725863397622629226309480836486427388484176463279384813974310500625102568341
n3 = 14215826065753265334521416948225868542990756976323308408298887797364519400310818641526401662106853573185085731682502059761982246604277475488691297554851873224516934619888327644352138127883043558424300092247604877819821625587944308487310522092440517150600171819145803937177931473336108429889165189521078678397694303305705260759351843006130968234071638035667854938070597400634242396852782331461576526836227336952718230741560369621645218729592233657856104560425642219241082727756696967324334634822771842625681505869025740662258929200756109704988223034840699133778958569054445520305361142302393767439478256174414187983763
c3 = 415916446053083522663299405080903121619846594209033663622616979372099135281363175464579440520262612010099820951944229484417996994283898028928384268216113118778734726335389504987546718739928112684600918108591759061734340607527889972020273454098314620790710425294297542021830654957828983606433731988998097351888879368160881316237557097381718444193741788664735559392675419489952796677690968481917700683813252460912749931286739585465657312416977086336732056497161860235343155953578618273940135486362350057858779130960380833359506761436212727289297656191243565734621757889931250689354508999144817518599291078968866323093
n4 = 12221355905532691305226996552124162033756814028292708728711809229588190407700199452617060657420166395065565154239801465361510672853972152857415394695376825120759202857555325904640144375262531345320714166285999668052224661520834318497234299585219832943519644095197479639328120838919035625832361810964127485907587199925564724081163804724975965691571850962714258888527902920462746795712011579424322515292865504642938090200503979483095345893697972170153990274670257331483858538617460680462369680572833191232126527727222302641204529110948993583190295067970240051042000918629138767209918572311469915774910003970381965123241
c4 = 2248834602646305164283014556051672824689884721514190813323189875541899566338153534858709617544459297836048770439230174669883719627734394673012731609952869246171300132019334542245094425654362711870373095782083791160029789553806741967408922001051006100049326921742208757147339981269528740944842177729701945606827918253016001436218891580980192743564642120923356793292885805519110411357830040053435569937296612987581482128241218218550319154933831743819546558930918761162723110000328532730751591375727881221199739397698390594797621758011191224528339478784930214820615602510460640307707682865125229937141010351138099874025
n5 = 18152103454920389919231636321286527841833809319334215885641536161086810144890443857211776387914779781628740172079478910188540146498426564211851629962338413488555121865779016981727229209606498886170396500155102635962395243364899026418106378234307821492609778555173516000309435730752571818439328803899462791834490025768785383592935046996428331508608555503567191807692523852530836008436655164751054189301721070209363416058642811329040202582026786024825518381761299547703962502636888833428457116986351812252188468878701301184044948733274488264320930936362549028124581962244201377136969591119942276742760215403738913067567
c5 = 2797812094994121597295362327809389195134238119144547570610194659000554967367804835006774413888965325870488368112707535584687083342412367127561646136089638402907513075405746055834487062923240856950047936297155455745928810738711368950139327254040579266046642851362228893522740216519732851152162928545416236075387903789535000820423985522550638100049857678600662008021574841083416323980817348573062083159710189689337626277009675683473560325178417766400002763719953723259300977655801234386662217462862844994462505601804422871991694828697337752697234180117437785537788728412520613916334045368736691714704501962513954509705
n6 = 22877887459293720334652698748191453972019668578065068224653972884599636421200068659750242304040301306798039254241668648594556654589309801728248683586229288074709849246660525799452637187132633064172425677552176203292787732404537215347782229753837476655088638984496409603054524994383358547132112778403912563916886533181616856401929346567686400616307916690806467019665390260267596320840786982457521423178851498130935577260638269429250197050326097193841333205073650802709022947551398142692735680419453533128176592587955634333425401930362881423044363132586170013458300714163531162544301477356808388416864173949089028317961
c6 = 12271947322974809255127222556723394446467844330408506340843897575503534175121932185624776713618037572593449207329510171212097269297133492090526270770286000839978630002819714376964416081198925899119135271459404333829811516667576167576916805217016117373027245648473458331936273975110163065432285322832123169216976420362833557809289561705091817949915218278430834098156335989014645979633658818904753942786129126233956314517292746008579152368541316795082120147520597254020266752859205131887527661767589367756335766220841483940854397440079467053684289006956034944336788288196391829411432383541473132962783883758561108297747
n7 = 19844333358004073542783728196775487079202832688982038135532362073659058674903791697765527614270399097276261983744620537925712167578187109058145015032736796457938148615396547198728652435169126585595701228287449135664667959433491335769206692390262797325133960778920452511673878233190120432257482339068405290918739453464061987163074129048150451046315248186376609350095502130018696275764450248681787926130463463923862832714969425813770847493135627599129546112143050369344208092649256659330284904392961574494907186727388685504929586018639846040474616307662546605623294842316524163106100888851228858194942825157286544846177
c7 = 9531264751315473345056673937611382755236533664089452852716992791452558274873158812669513178040971923528201631609089069182049526587423864397527252061341857426422965190913745048414029690931254119437249218321954899956104589066479231204536856131403590472063496956452030342299863907499976917750846369802185896519725837163530049157920978007252920334447236842959033879772444475877613295594785710745889554296655932909212643500877218304116451889820444820534937901427158918411546484157737612926382420354101675658160847653151539420222526999426483473829341628599881460824765758346670633385844187252696874025582747177333702736465
n8 = 16956880944655068255446705024149899655327230949463546092744762226005904114738078692036960935391303255804754787864713189658290361949509917704853428701870609882427423574672772606814823959758208695540116440342488334213300943604780971422918744381486937517952553797134323570131582724393100092308466968491068503301604506186521656059375518680612292667310641047190088814753025794048591445267711939066523165042651430468971452726568222388482323097260496415484997546126185688914792795834046855221759289007609518312601640548469651358391745947588643697900883634533872314566389446271647587564348026861264979727062157272541149018781
c8 = 16110326928338602237561005337578085623028116490564329920738844771341250444164294693848130674347672763073995755532723894042946521372321947507527854966013459795492930736187058535665041545095683801386814190612817128504426590828954205050425979880047802547011117626354405687170961272200066258220699329112978151044633994329352673342582175349200008181837211288847301836681860817044391028992501763375849046751094019224570802498414368189170656992427042010362385494565216988561215657424755648213390551881450141899860811844684546992754530755092358644968088017107313907435586729574798046187046145596726569637758312033849476689378
n9 = 16472195897077185060734002588086375750797253422014472876266294484788862733424113898147596402056889527985731623940969291811284437034420929030659419753779530635563455664549165618528767491631867637613948406196511848103083967995689432928779805192695209899686072900265108597626632371718430059561807147486376536203800038054012500244392964187780217667805308512187849789773573138494622201856638931435423778275004491853486855300574479177472267767506041000072575623287557610576406578525902565241580838652860552046216587141709709405062150243990097835181557208274750462554811004137033087430556692966525170882625891516050207318491
c9 = 11867731823522211833301190385669833752050387304375114576570892885641949969365352586215693183003550684262313893105989683214739695968039039944442567581277252581988489020834299896625977474857889570528169919064941042132119301236852358823696947330423679033138054012027878783478922023431469564210485180679933264749281963405243082505688901662659030897104957499953192201440290084373968716271056483463909282407034181891901928790601973222643210525000717355062752079302291729448234374709852429885984987094307177760741403086538949190424454337896501402430653783597070178968921411867485584517214777073301007918941216316241784521708
n10 = 13890749889361612188368868998653029697326614782260719535555306236512452110708495623964530174188871342332417484996749651846510646453983388637377706674890018646246874688969342600780781646175634455109757266442675502522791531161284420286435654971819525519296719668701529481662071464145515727217108362496784024871976015116522898184301395037566514980846499856316532479656908169681719288258287756566886281183699239684997698487409138330229321935477734921670373632304542254938831218652340699024011371979519574576890581492623709896310465567043899767342676912434857372520308852745792360420376574037705943820090308501053778144141
c10 = 6250115196713939477947942995075509357173312813431601073354390451609559579925704891503987992181988654989477525811826607070378476102616752398280691012244301950194800995432882828020405062344160270290542566163969692748126314259624623341922057435728127596172871894887055305291345372720594481096374310285437492746765510292863238933163142677773310305789984897974266961231555124787205980411992251387207335655129551950825339766848166539671565212408741432649813058363660321480995187545006718837863674527475323414266732366507905974800565463011676462244368010182725161416783875646259625352308599198614681446394427674340328493047
n11 = 21457499145521259498911107987303777576783467581104197687610588208126845121702391694574491025398113729462454256070437978257494064504146718372095872819969887408622112906108590961892923178192792218161103488204912792358327748493857104191029765218471874759376809136402361582721860433355338373725980783308091544879562698835405262108188595630215081260699112737457564998798692048522706388318528370551365364702529068656665853097899157141017378975007689790000067275142731212069030175682911154288533716549782283859340452266837760560153014200605378914071410125895494331253564598702942990036163269043699029806343766286247742865671
c11 = 6269656777204332618433779865483197625538144405832409880710764183039800286008967127279281167109250083159801218370191973055663058165456565194979210256278526713608759141588082614531352489547674696723140599892318118960648862531538435596775798128845789504910467783731144808685373807716609662688064728614003904579841055786083326311313295311152563668422289435606771091246147867715987583149743032723028324394173498623642539175178996531881058274717907066845565199058931743481410454382746158558886667761300257488769795092777021292335562818583719708133179974425584610403335487082478848975656282384575767178925517257692365828720

ns = [n1,n2,n3,n4,n5,n6,n7,n8,n9,n10,n11]
cs = [c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11]
for i in range(len(ns)-1):for j in range(i+1,len(ns)):if gcd(ns[i],ns[j]) != 1:print(i,j,gcd(ns[i],ns[j]))#2 10 147352146484643764031622970604294889624856525072751495442791038251325198568446104214691837421831622655415627526708110986526177662910836604556867226815780490826061784656230373978115117669691022691171484914452586975269776325816859478861737379536769555626991492537714713353640978988383143423169600280639641367257
p = gcd(n3,n11)
q = n3//p
d = invert(e, (p-1)*(q-1))
m = pow(c3,d,n3)
long_to_bytes(m)
#moectf{it_is_re@lly_@_signin_level_cryPto_ch@ll@nge_ng92WPIBung92WPIBun}

xorrrrr

单字节异或加密，key不清楚，爆破呗

flag = open('flag.txt','rb').read()
assert flag.startswith(b'moectf{') and flag.endswith(b'}')
article = open('article.txt','rb').read()import randomstrxor = lambda x,y: bytes([a^b for a,b in zip(x,y)])result = []for i in range(100):range_start = random.randint(0, len(article) - len(flag))mask = article[range_start:range_start + len(flag)]result.append(strxor(flag,mask))with open("result.log","w") as fs:fs.writelines([str(i)+"\n" for i in result])

msg = open('result.log').readlines()
msg = [eval(v) for v in msg]strxor = lambda x,y: bytes([a^b for a,b in zip(x,y)])msg.pop(93)flag = b'moectf{W0W_y0U_HaVe_mastered_tHe_x0r_0Peart0r!_0iYlJf!M3rux9G9Vf!JoxiMl}'for i in range(99):k = strxor(msg[i],flag)print(i,k, msg[i][len(flag): len(flag)+4])

ez_chain

from Crypto.Util.number import *with open("key.txt", "r") as fs:key = int(fs.read().strip())
with open("flag.txt", "rb") as fs:flag = fs.read().strip()
assert len(flag) == 72key = random.randint(base)
flag = b'moectf{1234567890}'
m = bytes_to_long(flag)base = bytes_to_long(b"koito")
iv = 3735927943def blockize(long):out = []while long > 0:out.append(long % base)long //= basereturn list(reversed(out))blocks = blockize(m)def encrypt_block_cbc(blocks, iv, key):encrypted = [iv]for i in range(len(blocks)):encrypted.append(blocks[i] ^ encrypted[i] ^ key)return encrypted[1:]print(encrypt_block_cbc(blocks, iv, key))

CBC的异或加密

from Crypto.Util.number import *def get_base(v,key):k = 0for i in v:k*=base k+=i^keyreturn long_to_bytes(k)enc = [8490961288, 122685644196, 349851982069, 319462619019, 74697733110, 43107579733, 465430019828, 178715374673, 425695308534, 164022852989, 435966065649, 222907886694, 420391941825, 173833246025, 329708930734]base = bytes_to_long(b"koito")
iv = 3735927943enc = [iv]+enc
enc_no_cbc = [enc[i-1]^enc[i] for i in range(1,len(enc))]
print(enc_no_cbc)
#[432674690023, 316083479432, 352306305703, 371107977111, 290734220940, 297123248011, 319994912423, 299600071333, 439506635169, 117796865187, 390928024701, 116328574846, 334545012049, 126344729644, 4910773519]#先猜长度
for kl in range(60,70):tkey = (bytes_to_long(b'moectf{')<<kl*8)//base**(len(enc_no_cbc)-1)tkey ^=enc_no_cbc[0]for i in range(-1000,1000):key = tkey + iv = get_base(enc_no_cbc, key)if b'moectf{' in v:print(kl, v)break#b'moectf{thE_c6c_Is_not_so_hard_9ifxi9i!JGofMJ36D9cPMxroif6!M6oSMuliPPcA3}'

flag_exchange

通过7次幂的加密，7太小了

from Crypto.Util.number import isPrime
from random import getrandbitswith open("flag.txt","rb") as fs:flag = fs.read().strip()def diffie_hellman(p, flag):alice_privKey = getrandbits(1024)alice_pubKey = pow(7, alice_privKey, p)bob_privKey = getrandbits(1024)bob_pubKey = pow(7, bob_privKey, p)superkey = pow(bob_pubKey, alice_privKey, p)m = int.from_bytes(flag, 'big')return (m * superkey) % p, alice_pubKey, bob_pubKeyfrom typing import Callabledef chall(input:Callable[[str],None], print:Callable[[str],None]):p = int(input("P = "))if isPrime(p) and p.bit_length() >= 1024:c, alice_pubKey, bob_pubKey = diffie_hellman(p, flag)print("Alice's public key: {}".format(alice_pubKey))print("Bob's public key: {}".format(bob_pubKey))print("Ciphertext: {}".format(c))else:print("Invalid P")

p = 148489452939627293978440608759173442996844898460634522907853247036287190215343795547617202268308624753445214064773770913426160349040708130179091977708205626736036279968938890838225633390629273742668246518422214765060312463614874340097452229306723297896927521825468282346196425145184245667794004328269609137340417ak = 13506505257902994926795380249835905035332235135211590669651308742167829046269285891449598193037355963934752767648404113487207650100033109025478128962303857858447936638923060635597426544104185868673581919643713670014001896204436868960342513827314899205480094036790812749085955676625407571768335193974649726494695
bk = 59201325930301080831020707685410323615662991813563685602352712666092170206124564190043221611539340845561303528216487138415532082769687060195426542753971585990425051581542903924039946519721877000739041825359986436864770793802041542615070727007409297662567507378880622382458757946880200666631006526627977012754315
cipher = 113859159624765890256820636097278078757726957717820539253273545045734749731324609285395064129161531586821631272409416097549974696104116207732168692060239798339988828548845153764394213384370110210010127665521461773892895483778273116595550989394557731721950223900029326813602085382207407781759070210822358775058078#c = (m * superkey) % p
a = discrete_log(ak,mod(7,p))
a = 64668307636287699049178361204443104904947965453137320623869437362374876996215394346912445893643403561894212148309122505028572486721984798507289505281507627944598519908420891989408013250242428623664747266752871230816411372152512197777858955459437623237541142998761716048619580286646790406108437435522991034889
#superkey = pow(bob_pubKey, alice_privKey, p)
s = pow(bk,a,p)
m = c*inverse_mod(s,p)%p#moectf{diffie_he11man_key_exChange_is_not_so_hard_2WPIBung92WPIBung9?WP}

giant_e

猜测是e非常d非常小的情况，用winner分解

from Crypto.Util.number import getPrimewith open("flag.txt","rb") as fs:flag = fs.read().strip()p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 0x609778981bfbb26bb93398cb6d96984616a6ab08ade090c1c0d4fedb00f44f0552a1555efec5cc66e7960b61e94e80e7483b9f906a6c8155a91cdc3e4917fa5347c58a2bc85bb160fcf7fe98e3645cfea8458ea209e565e4eb72ee7cbb232331a862d8a84d91a0ff6d74aa3c779b2b129c3d8148b090c4193234764f2e5d9b2170a9b4859501d07c0601cdd18616a0ab2cf713a7c785fd06f27d68dff24446d884644e08f31bd37ecf48750e4324f959a8d37c5bef25e1580851646d57b3d4f525bc04c7ddafdf146539a84703df2161a0da7a368675f473065d2cb661907d990ba4a8451b15e054bfc4dd73e134f3bf7d8fa4716125d8e21f946d16b7b0fc43
m = int.from_bytes(flag,"big")
c = pow(m,e,n)n = 0xbaa70ba4c29eb1e6bb3458827540fce84d40e1c966db73c0a39e4f9f40e975c42e02971dab385be27bd2b0687e2476894845cc46e55d9747a5be5ca9d925931ca82b0489e39724ea814800eb3c0ea40d89ebe7fe377f8d3f431a68d209e7a149851c06a4e67db7c99fcfd9ec19496f29d59bb186feb44a36fe344f11d047b9435a1c47fa2f8ed72f59403ebb0e439738fd550a7684247ab7da64311690f461e6dce03bf2fcd55345948a3b537087f07cd680d7461d326690bf21e39dff30268cb33f86eeceff412cd63a38f7110805d337dcad25e6f7e3728b53ca722b695b0d9db37361b5b63213af50dd69ee8b3cf2085f845d7932c08b27bf638e98497239
c = 0x45a9ce4297c8afee693d3cce2525d3399c5251061ddd2462513a57f0fd69bdc74b71b519d3a2c23209d74fcfbcb6b196b5943838c2441cb34496c96e0f9fc9f0f80a2f6d5b49f220cb3e78e36a4a66595aa2dbe3ff6e814d84f07cb5442e2d5d08d08aa9ccde0294b39bfde79a6c6dcd2329e9820744c4deb34a039da7933ddf00b0a0469afb89cba87490a39783a9b2f8f0274f646ca242e78a326dda886c213bc8d03ac1a9150de4ba08c5936c3fe924c8646652ef85aa7ac0103485f472413427a0e9d9a4d416b99e24861ca8499500c693d7a07360158ffffa543480758cafff2a09a9f6628f92767764fa026d48a9dd899838505ae16e38910697f9de14
e = 0x609778981bfbb26bb93398cb6d96984616a6ab08ade090c1c0d4fedb00f44f0552a1555efec5cc66e7960b61e94e80e7483b9f906a6c8155a91cdc3e4917fa5347c58a2bc85bb160fcf7fe98e3645cfea8458ea209e565e4eb72ee7cbb232331a862d8a84d91a0ff6d74aa3c779b2b129c3d8148b090c4193234764f2e5d9b2170a9b4859501d07c0601cdd18616a0ab2cf713a7c785fd06f27d68dff24446d884644e08f31bd37ecf48750e4324f959a8d37c5bef25e1580851646d57b3d4f525bc04c7ddafdf146539a84703df2161a0da7a368675f473065d2cb661907d990ba4a8451b15e054bfc4dd73e134f3bf7d8fa4716125d8e21f946d16b7b0fc43

from Crypto.Util.number import long_to_bytes,bytes_to_long
def transform(x,y):res = []while y:res.append(x//y)x,y = y,x%yreturn resdef continued_fraction(res):numerator,denominator = 1,0for i in res[::-1]:denominator,numerator = numerator,i*numerator+denominatorreturn numerator,denominatordef wiener_attack(c,res,n):print("Attack start...")for i in range(1,len(res)):ress = res[:i]d = continued_fraction(ress)[1]m = long_to_bytes(pow(c,d,n))print(m)if all(0x20<=k<=0x7f for k in m):#if b'flag{' in m:print(m)breakres = transform(e,n)
wiener_attack(c,res,n)
#moectf{too_larGe_exponent_is_not_a_iDea_too!_Bung92WPIBung92WPIBung9?WP}

minipack

远看是背包加密，但是没取模

import randomwith open("flag.txt", "rb") as fs:flag = fs.read().strip()assert len(flag) == 72
m = int.from_bytes(b"\xff" + flag + b"\xff", "big")def long2bits(long):bits = []while long > 0:bits.append(long & 1)long >>= 1return list(reversed(bits))def genkey(len):sum = 0out = []for i in range(len):delta = random.randint(1, 10000)x = sum + deltaout.append(x)sum += xreturn outkey = genkey(74 * 8)with open("key.txt", "w") as fs:fs.write(str(key))def encrypt(m, keys):data = long2bits(m)assert len(data) == len(keys)return sum((k if (p == 1) else 1) for p, k in zip(data, keys))with open("ciphertext.txt", "w") as fs:fs.write(str(encrypt(m, key)))

直接一个个减就行，不够就是0，够就是1

from key import key
from Crypto.Util.number import *c = 44096612931024003148407895164090667174657344536623354666642108463093659898867859567157728084018394988840266329206836985537987081415020571845239234014695335928717091578810470705259929
m = ''
for k in key[::-1]:if c>=k:c-=k m+='1'else:m+='0'flag = int(m[::-1],2)
print(long_to_bytes(flag))
#moectf{superiNcreasiNg_sequeNce_is_useful_tO_cONstruct_a_KNapsacK_MAxSM}

bad_random

LCG加密，先用grobner基求参数，再解

import randomwith open("flag.txt", "r") as f:flag = f.read().strip()class LCG:def set_params(self):self.m = random.randint(10000, 20000)self.a = random.randint(10000, 20000)self.c = random.randint(1, self.a-1)self.x = random.randint(0, self.m-1)def get_all_output(self):x0 = self.xs = set()while (t := self()) not in s:s.add(t)self.x = x0return sdef __init__(self):self.set_params()while len(self.get_all_output()) < 10:self.set_params()def __call__(self):self.x = (self.a * self.x + self.c) % self.mreturn self.xfrom typing import Callabledef chall(input:Callable[[str],None], print:Callable[[str],None]):from hashlib import md5from string import ascii_letterss = "".join(random.choices(ascii_letters, k=16))h = md5(s.encode()).hexdigest()print(f"<!> md5(XXXXXXXX+{s[8:]}) == {h}")i = input("Give me XXXXXXXX: ")if md5((i + s[8:]).encode()).hexdigest() != h:print("<!> ACCESS DENIED <!>")returninst = LCG()print("Let's play a simple game! If you can guess the right number, I will give your the flag! You have 10 tries")for tries in range(10):i = input(f"Give me a number, you have failed for {tries} times: ")if int(i) == (right := inst()):print(f"Congurations! You win the game! Your flag is here: {flag}")else:print(f"Oh, you are wrong! The right number is {right}")

from pwn import *
from hashlib import md5 
import string 
from math import gcd 
from gmpy2 import invert io = remote('127.0.0.1', 11027)
context.log_level = 'debug'io.recvuntil(b'md5(XXXX+')
tail = io.recvuntil(b') == ', drop = True)
hash = io.recvline().strip().decode()#proof
found = iters.bruteforce(lambda x: md5(x.encode() + tail).hexdigest() == hash, string.ascii_letters, 4)
io.sendlineafter(b"XXXX: ", found.encode())xs = []
for _ in range(9):io.sendlineafter(b"times: ", b'88')io.recvuntil(b'The right number is ')xs.append(int(io.recvline()))print(f"{xs = }")
#'''
P.<a,c> = PolynomialRing(ZZ)
F = []
for i in range(1, 9):f = xs[i-1]*a + c - xs[i]F.append(f)I = Ideal(F).groebner_basis()
print(I)
# 求解参数a c m  : x = (ax+c) %m
res=[x.constant_coefficient() for x in I]
m = res[2]
a = -res[0]%m
c = -res[1]%m
for a in range(10000,20000):if xs[-1] == (xs[-2]*a+c)%m:print((xs[-1]*a+c)%m)break
'''x10 = input('x10:')
#print(b's'+x10.encode())
io.sendlineafter(b"times: ", x10.encode())
io.recvline()
io.interactive()
#moectf{u5e_5ingle_lcg_a5_a_RanDoM_nuMbeR_geneRaToR_i5_noT_a_gooD_iDea!_}\n'

broken_hash

自制的hash，换个顺序还能得到相同值。

def F(x, y, z):return ((x & ~y) ^ (y & ~z) ^ (z & ~x)) ^ (((x + y) * (y + z) + (x + z)) & 0xFFFF_FFFF_FFFF_FFFF_FFFF_FFFF_FFFF_FFFF)def _block_hash(a, b, c, d):x, y, z, w = F(a, b, c), F(b, c, d), F(c, d, a), F(d, a, b)return (a ^ b ^ c ^ d ^ x ^ y ^ z ^ w) ^ 0xFFFF_FFFF_FFFF_FFFF_FFFF_FFFF_FFFF_FFFFdef _hash(blocks: list[int]):length = len(blocks)if length % 4 != 0:padding = 4 - length % 4blocks += [0] * paddinglength += paddingif length == 4:return _block_hash(*blocks)else:block_size = length // 4h1 = _hash(blocks[:block_size])h2 = _hash(blocks[block_size : block_size * 2])h3 = _hash(blocks[block_size * 2 : block_size * 3])h4 = _hash(blocks[block_size * 3 :])return _block_hash(h1, h2, h3, h4)def bytes2blocks(data: bytes, block_size=16):if len(data) % block_size != 0:data += b"\x00" * (block_size - len(data) % block_size)return [int.from_bytes(data[i : i + block_size], "little")for i in range(0, len(data), block_size)]def hash(*data: list[bytes]):return _hash(bytes2blocks(b"".join(data)))from typing import Callable
from random import randbytes
from base64 import b64decode,b64encode
from hashlib import md5
from string import ascii_letters
from random import choiceswith open("flag.txt", "r") as f:flag = f.read().strip()def chall(input: Callable[[str], None], print: Callable[[str], None]):def proof_of_work():s = "".join(choices(ascii_letters, k=16))h = md5(s.encode()).hexdigest()print(f"<!> md5(XXXXXXXX+{s[8:]}) == {h}")i = input("Give me XXXXXXXX: ")return md5((i + s[8:]).encode()).hexdigest() == hif not proof_of_work():print("<!> ACCESS DENIED <!>")returnb = randbytes(256)print(f"this is a random bytes: {b64encode(b).decode()}")i = input("give me another bytes with the same hash: ")try:d = b64decode(i)except:print("invaild input")if hash(b) == hash(d) and d!=b:print(f"congurations! and your flag is {flag}")

from pwn import *
from base64 import * 
from hashlib import md5 io = remote('127.0.0.1', 10946)
context.log_level = 'debug'io.recvuntil(b'md5(XXXX+')
tail = io.recvuntil(b') == ', drop = True)
hash = io.recvline().strip().decode()#proof
found = iters.bruteforce(lambda x: md5(x.encode() + tail).hexdigest() == hash, string.ascii_letters, 4)
io.sendlineafter(b": ", found.encode())io.recvuntil(b"this is a random bytes: ")
b = b64decode(io.recvline().strip())a = b[16:64] + b[:16] + b[64:]
a64 = b64encode(a)io.sendlineafter("give me another bytes with the same hash: ", a64)print(io.recvline())
io.interactive()
#moectf{a_hash_FUNCtioN_With_sYMMEtRY_is_vERY_vUlNERa6lE_3iiA0JiuP0DxuuP}

factorize_me!

给了9个因子的N和对应的phi，从中选3个作n加密，先用多因子分解得到因子，再找出是哪个

from Crypto.Util.number import getPrime
from math import prod
from sympy import nextprime
from random import choiceswith open('flag.txt', 'rb') as fs:flag = fs.read().strip()primes = [getPrime(512) for _ in range(9)]
print(f"{prod(primes) = }")
print(f"{prod(p - 1 for p in primes) = }")primes2 = [nextprime(p) for p in choices(primes, k=3)]
n = prod(primes2)
e = 65537
c = pow(int.from_bytes(flag, 'big'), e, n)print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')

from Crypto.Util.number import *
from gmpy2 import *N =  363364907814244019888662301376841344262476227242899756862391470731421569394957444030214887114615748277199649349781524749919652160244484352285668794188836866602305788131186220057989320357344904731322223310531945208433910803617954798258382169132907508787682006064930747033681966462568715421005454243255297306718356766130469885581576362173340673516476386201173298433892314145854649884922769732583885904512624543994675379894718657682146178638074984373206937523380103438050549181568015985546172618830480078894445808092527561363650503540062128543705172678754195578429520889784813733491180748361345720247750720179608752244490362713103319685024237941527268458213442611663415417005556439749055222361212059968254748751273361732365487788593341859760309778894350385339764442343374673786357175846291309425081492959910254127778240522152676060766139057453197528944251599979227271074508795482632471242983094008619339488744362509349734218480932255216087706001484182136783834973304870508270118505737767002256270427907341952256516206663258530300791364944105025764611810001781971638030661367630116818647252727909489405550104641122269772492252464714694507693447974171377200402508765841829763548525530878309985480248379655169722567051495205792089930014228403456098065971372039443284193603395249634283366194562380309469628114581468645669390610963076340643757972439104287127375438663839421605531570285615180251
phi =  363364907814244019888662301376841344262476227242899756862391470731421569394957444030214887114615748277199649349781524749919652160244484352285668794188836492373364350673588273863828369502073826782362255108313852264064760467561392054178047091483873483255491431451728274259516789065331176728192953741805933100379191778599394515981288225535175013258094287912195847642598436035132783919453991516358280321085873745330313812205910011387125778714795906023110368957596998222544234082487264006696812862179916726781327290284827659294751262185328816323311831349296593013038823107653943652771448719760448938995150646738377177532550757319539185878535087009904848382493668686831331474113789651777885239747000076063679062106375348803749466079052774597412239427050432901553466002731972993029311850718200685157193170716432600165476733200831046297530470544781309612128231925681374239849452623513538498417735984094919756374577623486416462101457492789215144166273775249387638107644634704270216130852885082174564648445147377239033930079759024399532146184753110240154062693457622208373371290126810856885343328090305620627668495081760346853701632815149478447405718664667978825807101325764916405446176183238866136433205933785973568759281210319422288153910340542098573782006262190181726245838857185687242960093445000287347616796984610291664809895901301187179157382169999966124177588884152267266994164841066291200
n = 899081756851564072995842371038848265712822308942406479625157544735473115850983700580364485532298999127834142923262920189902691972009898741820291331257478170998867183390650298055916005944577877856728843264502218692432679062445730259562784479410120575777748292393321588239071577384218317338474855507210816917917699500763270490789679076190405915250953860114858086078092945282693720016414837231157788381144668395364877545151382171251673050910143023561541226464220441
e = 65537
c = 841335863342518623856757469220437045493934999201203757845757404101093751603513457430254875658199946020695655428637035628085973393246970440054477600379027466651143466332405520374224855994531411584946074861018245519106776529260649700756908093025092104292223745612991818151040610497258923925952531383407297026038305824754456660932812929344928080812670596607694776017112795053283695891798940700646874515366341575417161087304105309794441077774052357656529143940010140from math import gcd
from random import randrange
def factorize_multi_prime(N, phi):"""Recovers the prime factors from a modulus if Euler's totient is known.This method works for a modulus consisting of any number of primes, but is considerably be slower than factorize.More information: Hinek M. J., Low M. K., Teske E., "On Some Attacks on Multi-prime RSA" (Section 3):param N: the modulus:param phi: Euler's totient, the order of the multiplicative group modulo N:return: a tuple containing the prime factors"""prime_factors = set()factors = [N]while len(factors) > 0:# Element to factorize.N = factors[0]w = randrange(2, N - 1)i = 1while phi % (2 ** i) == 0:sqrt_1 = pow(w, phi // (2 ** i), N)if sqrt_1 > 1 and sqrt_1 != N - 1:# We can remove the element to factorize now, because we have a factorization.factors = factors[1:]p = gcd(N, sqrt_1 + 1)q = N // pprint(p)if is_prime(p):prime_factors.add(p)elif p > 1:factors.append(p)if is_prime(q):prime_factors.add(q)elif q > 1:factors.append(q)# Continue in the outer loopbreaki += 1return list(prime_factors)n_factors = factorize_multi_prime(N,phi)
n_factors = sorted(n_factors)#[6811480804433459752827714558479851837166061762294131563310130325846430072816177165149613687307165209577130630311477665591141650399740741396784593477667511,6991223361118904775931217829045348785013077549030883418924453538830605687999480005714979700653172534877541317997174968789510984315425270755055110913347281, 7592439908930473591169395506464664967460880934907692099467559610659035874008829133810341129161864445676397227262130671224157308868678442281617413952593477, 7661276973316857207751367277881032536449069939447322837508906694964933673171693624171780997296797446643574508184011878230465391879808258241752897792891323, 8752762682421281693932454897190422008900505775990831144558827755415243453970083322530846132571648469860763497724505255094464743633789884168771246977571539, 9987009117206906203158749743824168660291275882852229158070368815160479543708376165641735042845357978292384303332559592302507789120810447986634662721490507, 10022455487144667211701100343824680124338467215246658405697280466931561838565228778624923751405642974058833143888323468902504576610147119708725877528011439, 11627877395179828773706504422918933052041685770731872812302758181943244472706231518350716590168708806854971155512042158777017234038219076771501368374236727, 12876877424944854147075816504195994138450356002779004886384584287813869165469217718717854027672044903401715370348223932937626725119320180795716270261309139]for t in n_factors:for i in range(2000):if gcd(t+i, n) != 1:print(t+i)p = [6991223361118904775931217829045348785013077549030883418924453538830605687999480005714979700653172534877541317997174968789510984315425270755055110913347349,
9987009117206906203158749743824168660291275882852229158070368815160479543708376165641735042845357978292384303332559592302507789120810447986634662721490849,
12876877424944854147075816504195994138450356002779004886384584287813869165469217718717854027672044903401715370348223932937626725119320180795716270261309141]phi = (p[0]-1)*(p[1]-1)*(p[2]-1)
d = inverse_mod(e,phi)
m = pow(c,d,n)
long_to_bytes(int(m))#moectf{you_KNow_how_to_faCtorize_N_right?_9?WPIBung6?WPIBung6?WPIBund6?}

feistel_promax

from Crypto.Util.number import *
from os import urandomround = 2
flag = open("./secret", "rb").read().strip()def f(m, key):m = m ^ (m >> 4)m = m ^ (m << 5)m = m ^ (m >> 8)m ^= keym = (m * 1145 + 14) % 2**64m = (m * 1919 + 810) % 2**64m = (m * key) % 2**64return mdef enc(m, key, round):key = bytes_to_long(key)left = bytes_to_long(m[:8])right = bytes_to_long(m[8:])for i in range(round):left, right = right, f(right, key) ^ leftleft, right = right, leftreturn long_to_bytes(left).rjust(8, b"\x00") + long_to_bytes(right).rjust(8, b"\x00")def padding(m):mlen = len(m)pad = 16 - mlen % 16return m + pad * bytes([pad])def ecb_enc(m, key):m = padding(m)mlen = len(m)c = b""for i in range(mlen // 16):c += enc(m[i * 16 : i * 16 + 16], key, round)return ckey = urandom(8)print(ecb_enc(padding(flag), key))
# b'B\xf5\xd8gy\x0f\xaf\xc7\xdf\xabn9\xbb\xd0\xe3\x1e0\x9eR\xa9\x1c\xb7\xad\xe5H\x8cC\x07\xd5w9Ms\x03\x06\xec\xb4\x8d\x80\xcb}\xa9\x8a\xcc\xd1W\x82[\xd3\xdc\xb4\x83P\xda5\xac\x9e\xb0)\x98R\x1c\xb3h'

很麻烦

from Crypto.Util.number import long_to_bytes as l2b, bytes_to_long as b2ldef f(m, key):m = m ^ (m >> 4)m = m ^ (m << 5)m = m ^ (m >> 8)m ^= keym = (m * 1145 + 14) % 2**64m = (m * 1919 + 810) % 2**64m = (m * key) % 2**64return mdef enc(m, key, round):key = b2l(key)left = b2l(m[:8])right = b2l(m[8:])for i in range(round):left, right = right, f(right, key) ^ leftleft, right = right, leftreturn l2b(left).rjust(8, b"\x00") + l2b(right).rjust(8, b"\x00")'''
key = b'\xcdU\x19\xb4\x04\x9f\xaaE'
flag = b'0123456789abcdef}'
for i in range(1,17):tmp = flag + bytes([i])*i tmp = tmp[-16:]c = enc(tmp,key,2)print(c)b'\xa0\x8b\x9b\xce\xe4\xc8\xc2l<^\xfc\xe1\x8b\xb8\xbe\xd1'
b'\x82Z\x13o\x92!\xf7V\xa7\n\x03!\x8b\xe2\x0f\x1e'
b'\x1f<\xb8\x15c\xce\x84\x87\xb5\x91\xea\xb3\xc6\xe0S\x97'
b'\x82nW\x12\xb8I\xe1\x81^Z\xdc\xc0\xba\xde\xdd\xb0'
b'!\xd3\x84Vh~\xa7\x01\x1b\xb7u\xad\x92\xeb\xb6\xfd'
b'Un\x1d\xf2\nzg\xc0F|*\xa7\xadX\xf0"'
b',\x83\x91\xacs@V\x13\x08\x17\xc6\xdb81\xcfk'
b'\x80_-S\xa3\xd1S\xa7\xad\xc2\xb8W\xb5\xaeju'
b'\r\xc7Z\xcbh}\x14\xf7\xa4\xc23s8\x83\\\xc7'
b'1u\xb4\x90\x8c\t\x16\xb0P\xc9\x8a\n\xdf\xeb\xeav'
b'\r\xad\xfd\xe1\x8a.P\xac\xb4\xc3\x0148\xbb\xfdI'
b'\xce3\xeb\t\x82\xc3K[<\xf0\xd7\xc2\x0e?o,'
b'\xa7+\x88.K\xee\x8be\xec\xf4Z\xac\x83@u\xeb'
b';8q}\x07\x069\xfeh\xe1\xcb\xf7\xe7\xf19\x9a'
b'\xa2\xf1r\x90\xf9\xd4k\x8c\xce\x964\xd3y\x16BU'
b'\x81\xb9\xa1d\xac\xac\x81:Q\x12\xcb\xe4S1n\x91'
'''
'''
l         r                  plain
r         f(r)^l             round 1
f(r)^l    f(f(r)^l)^r        round 2
f(f(r)^l)^r   f(r)^l         c
''''''
#test
l = b2l(b'\x10'*8)
r = b2l(b'\x10'*8)
key = b2l(b'\xcdU\x19\xb4\x04\x9f\xaaE')
fr = f(r,key)^l
ffr = f(fr,key)^r
print(l2b(fr),l2b(ffr))
'''
enc = b'B\xf5\xd8gy\x0f\xaf\xc7\xdf\xabn9\xbb\xd0\xe3\x1e0\x9eR\xa9\x1c\xb7\xad\xe5H\x8cC\x07\xd5w9Ms\x03\x06\xec\xb4\x8d\x80\xcb}\xa9\x8a\xcc\xd1W\x82[\xd3\xdc\xb4\x83P\xda5\xac\x9e\xb0)\x98R\x1c\xb3h'#c = b'\x81\xb9\xa1d\xac\xac\x81:Q\x12\xcb\xe4S1n\x91'
c = enc[-16:]
cl,cr = b2l(c[8:]), b2l(c[:8])   #cl和r取3字节，l取2字节
#print(l2b(cl),l2b(cr))
'''
for pad in range(1,17):l = bytes([pad])*2r = bytes([pad])*3l,r = b2l(l),b2l(r)for key8 in range(256):for key7 in range(256):key = (key7<<8) |key8fr  = (f(r,  key)^l) &0xffffffr = (f(cl, key)^r) &0xffffif fr == cl&0xffff and ffr == cr&0xffff:print(pad, hex(key7), hex(key8) )
'''
#pad 16  key = b'\xac\xb4'
pad = 16
key_tail = b'4t*zFD\xac\xb4'
'''
mod = 1<<(8*(len(key_tail)+1))
l = bytes([pad])*8
r = bytes([pad])*8
l,r = b2l(l),b2l(r)
for k in range(256):key = (k<<(8*len(key_tail)))|b2l(key_tail)fr  = (f(r,  key)^l) %modffr = (f(cl, key)^r) %modif fr == cl%mod and ffr == cr%mod:print(l2b(key) )
'''
key = b2l(key_tail )
#从明文 
c = enc[32:48]
cl,cr = b2l(c[8:]),b2l(c[:8])
r = f(cl,key)^cr
l = f(r,key)^cl
print(l2b(l)+l2b(r))#moectf{F_func_1s_n1t_Ve5y_$EcU%e}