目录
1.B树
2.B+树和B树的不同
3.B*树
B树较于哈希红黑树的优势:外查找:读取磁盘数据 ; B树的高度更低,对磁盘的进行I/O操作的次数更少(磁盘的性能比内存差得多);
1.B树
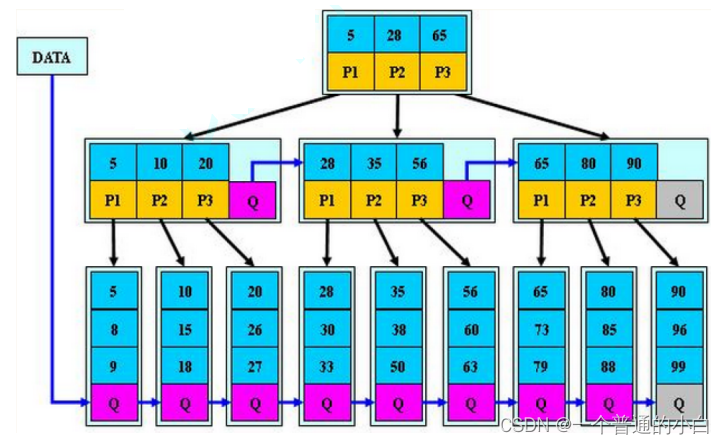
1.1.B树的概念:
- 根节点至少有两个孩子 (空树除外)
- 每个分支节点都包含k-1个关键字和k个孩子,其中 ceil(m/2) ≤ k ≤ m ceil是向上取整函数 (分支节点都是依靠叶节点分裂得到,孩子依靠分裂得到)
- 每个叶子节点都包含k-1个关键字,其中 ceil(m/2) ≤ k ≤ m (叶子节点没有孩子)
- 所有的叶子节点都在同一层 (因为分裂向上插入)
- 每个节点中的关键字从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分 ( 所有左孩子 < 关键字 < 所有右孩子 )
- 每个结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)其中,Ki(1≤i≤n)为关键子,且Ki < Ki+1(1<= i <= n-1) Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。
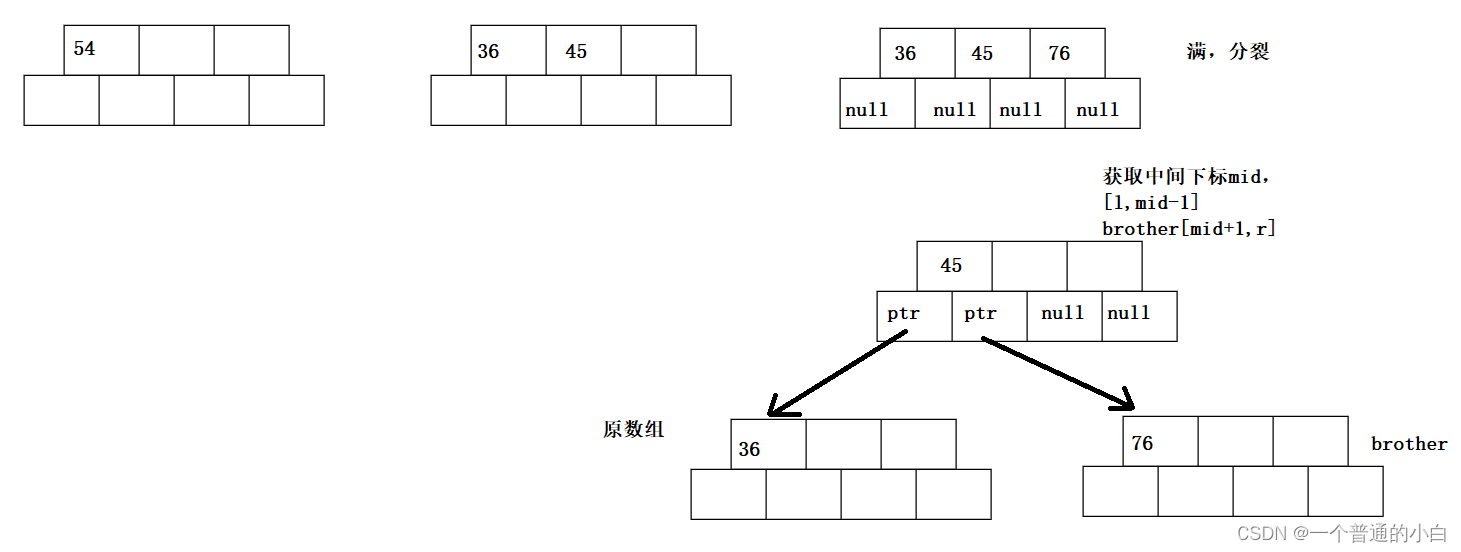
分裂:所有元素都是插入关键字,孩子是指向的节点指针;数组满了,分裂出brother(new出来)节点将【mid+1,r】拷贝给brother,如果父节点为空就,创建新的父节点,父节点的左边为原数组,有孩子为brother;
#pragma once
#include<iostream>
#include<vector>using namespace std;template<class T, size_t N>
class Node {public:Node(){//孩子最多为N个,关键字比孩子少一个//需要多开辟一个,来判断数组元素满_key.resize(N);_children.resize(N+1, nullptr);_parent = nullptr;_size = 0;}~Node(){}
public://关键字vector<T> _key;//孩子数据vector<Node<T, N>*> _children;//父亲节点Node<T, N>* _parent;//有效个数size_t _size;
};
template<class T, size_t N>
class BTree {
public:typedef Node<T, N> Node;//返回节点和下标pair<Node*, int> Find(T val){Node* parent = nullptr;Node* cur = _root;//找到合适位置,从左向右找 比当前元素大,判断是否有左孩子while (cur){size_t i = 0;while (i < cur->_size){//找到比我大的了if ( val < cur->_key[i] )break;else if ( val > cur->_key[i] )i++;else//元素存在了,退出return make_pair(cur, i);}//保存父亲parent = cur;cur = cur->_children[i];}//不存在,返回父亲和-1return make_pair(parent, -1);}void _Insert(T val, Node* parent, Node* child){int end = parent->_size - 1;//从最后一个元素挪数据while (end >= 0){//目标元素更小,挪if (val < parent->_key[end]){parent->_key[end + 1] = parent->_key[end];parent->_children[end + 2] = parent->_children[end + 1];//挪右孩子end--;}elsebreak;}//合适的插入位置parent->_key[end + 1] = val;parent->_children[end + 2] = child;//右孩子if (child)//指向父亲child->_parent = parent;parent->_size++;}bool Insert(T val){//第一个插入的元素if (_root == nullptr){_root = new Node;_root->_key[0] = val;_root->_size++;}else{//查找是否存在pair<Node*, int> pr = Find(val);if (pr.second >= 0)//元素已存在,不用在插入return false;//该插入的位置Node* parent = pr.first;Node* child = nullptr;_Insert(val, parent, child);while (true){if (parent->_size < N)return true;else//数组满,分离{//分裂 [l, mid-1] [mid+1, r]int mid = N / 2;size_t i = 0;size_t j = mid + 1;//分离兄弟节点Node* brother = new Node;for (; j < N; j++, i++){brother->_key[i] = parent->_key[j];brother->_children[i] = parent->_children[j];//有孩子节点,brother做新父亲if (parent->_children[j])parent->_children[j]->_parent = brother;//分裂给兄弟的关键字和孩子置空parent->_children[j] = nullptr;parent->_key[j] = T();}//还有一个右孩子给brotherbrother->_children[i] = parent->_children[j];if (parent->_children[j])parent->_children[j]->_parent = brother;parent->_children[j] = nullptr;//分裂完处理个数;brother->_size = i;parent->_size -= (i + 1);//减去兄弟和中间//中间值向上插入T midKey = parent->_key[mid];parent->_key[mid] = T();//头节点if (parent->_parent == nullptr){_root = new Node;_root->_key[0] = midKey;_root->_children[0] = parent;_root->_children[1] = brother;_root->_size = 1;//孩子的父亲为头parent->_parent = _root;brother->_parent = _root;break;}else{//非头重新插入_Insert(midKey, parent->_parent, brother);//继续循环,看上一层是否满了parent = parent->_parent;}}}}}
public:
private:Node* _root = nullptr;
};测试代码:
#include"BTree.h"
void TestBtree()
{int a[] = { 53, 139, 75, 49, 145, 36, 101 };BTree<int, 3> t;for (auto e : a){t.Insert(e);}
}
int main()
{TestBtree();
}2.B+树和B树的不同
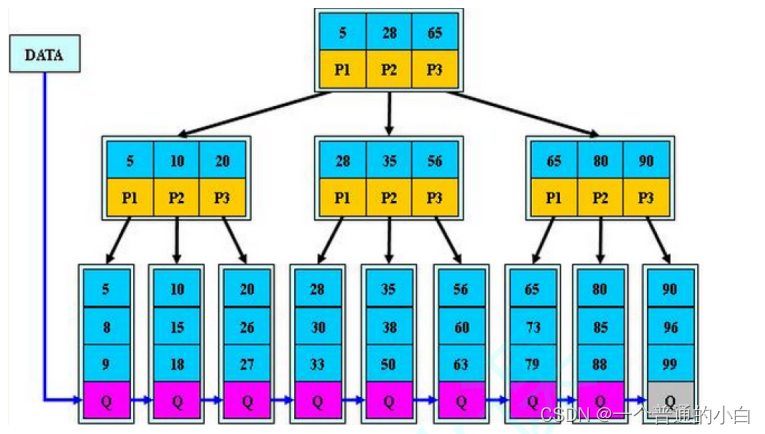
- 分支节点的子树指针与关键字个数相同
- 分支节点的子树指针p[i]指向关键字值大小在[k[i],k[i+1])区间之间
- 所有叶子节点增加一个链接指针链接在一起
- 所有关键字及其映射数据都在叶子节点出现
B+树的特性:
- 所有关键字都出现在叶子节点的链表中,且链表中的节点都是有序的。
- 不可能在分支节点中命中。
- 分支节点相当于是叶子节点的索引,叶子节点才是存储数据的数据层。
3.B*树
B*树是B+树的变形,在B+树的非根和非叶子节点再增加指向兄弟节点的指针。
区别就是分裂方式不同:不同当前节点和下一个兄弟节点都满才分裂,都区1/3构成一个new节点,提高利用率, 最多3/1被浪费;