1、常见的泰勒展开公式
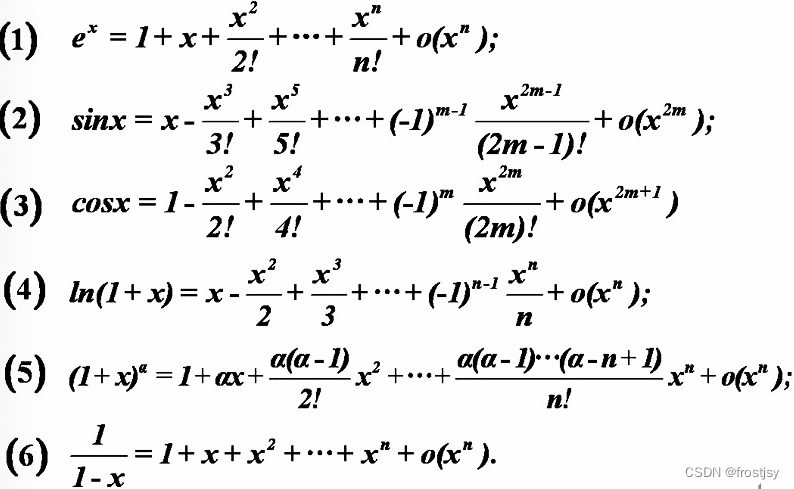
2、polyloss引入动机
2.1、polyloss定义
polyloss通过泰勒展开来逼近损失函数的简单框架,将损失函数设计为多项式函数的线性组合
2.2、polyloss主要贡献
提出了一个新的框架来理解和设计损失函数
PolyLoss可以让多项式基根据目标任务和数据集进行调整
3、polyloss具体内容
3.1、cross-entory、focal-loss的泰勒展开式
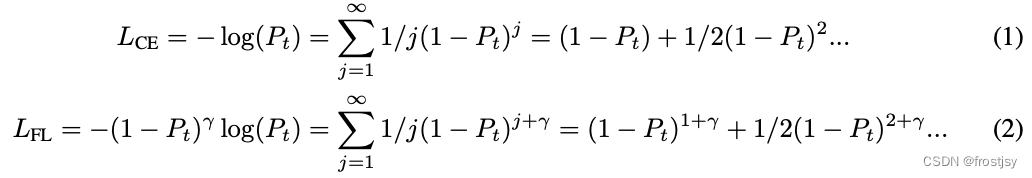
3.2、cross-entropy、focal loss和polyloss的统一视图
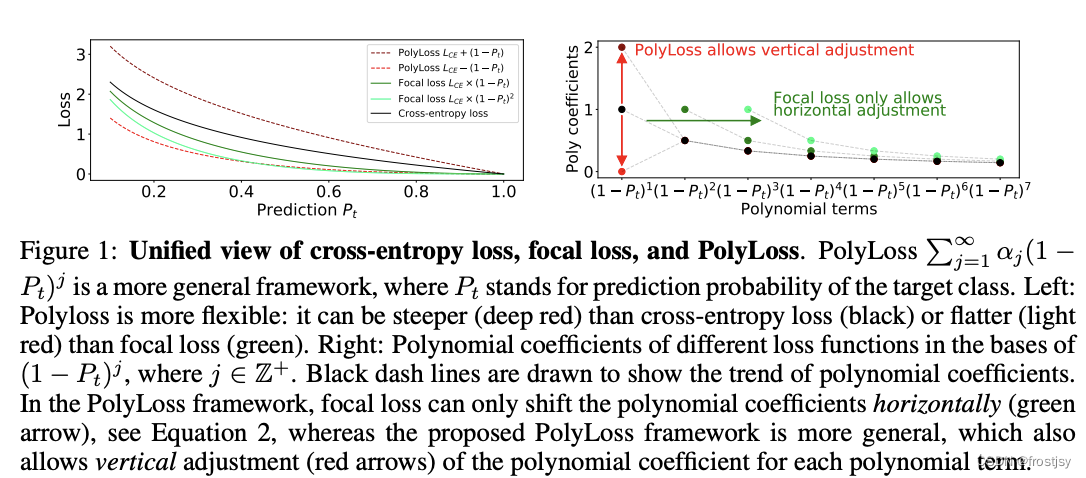
cross-entropy、foacl loss以及polyloss的统一视图主要讨论了,polyloss的灵活性。
polyloss可以比cross-entropy更加陡峭或比focal loss更加平滑 。focal loss泰勒展开式,多项式因子只能水平移动(右图绿色箭头),新框架下的polyloss支持垂直移动(右图红色箭头)。
3.3、不同loss通过polyloss框架展开

以cross-entropy为例,在polyloss框架下,cross-entropy有4种展开形式。1、原始的泰勒展开式;2、去掉泰勒展开式的高阶项;3、引入超参的polyloss-n框架;4、polyloss-n特例,n=1时的polyloss-1 。
3.4、基于交叉熵对比N值的选择对loss的影响

(a)图显示,cross-entropy的泰勒展开式,只有在n取得较大的情况下,才能达到和cross-entory等效的效果。(b)图显示,调整学习率对并未提升
的分类效果,在lr=0.1时,获得了最好的效果。
3.5、poly-n
3.5.1、poly-n结构
为了能灵活调整多项式的权重,变更多项式为如下结构:


3.5.2、poly-n效果对比

图(a)讨论了准确率随变化的情况,当
=1时,准确率越来越平缓。图(b)讨论了polyloss展开式第一项对梯度的贡献,其贡献至少占了65%。
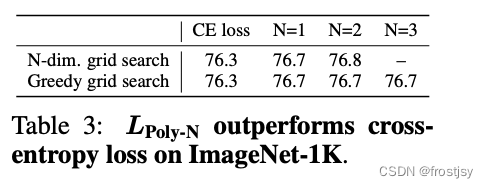

n阶网格搜索,探索n对polyloss结构的影响。
4、polyloss效果对比
4.1、提速
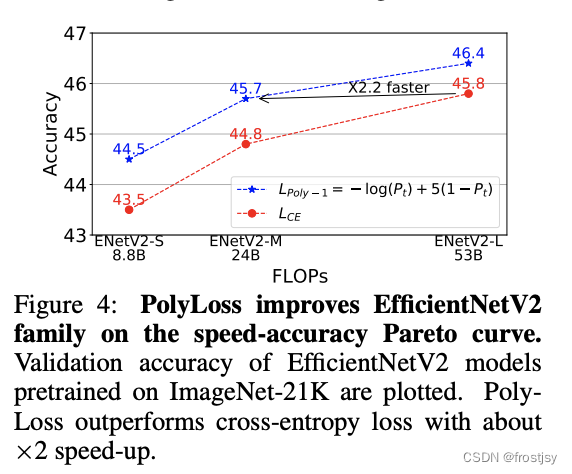
达到相同的效果,polyloss比cross-entropy快了2倍。
4.2、2d-图像分类任务上效果对比
4.2.1、多项式中 对准确率的影响
对准确率的影响
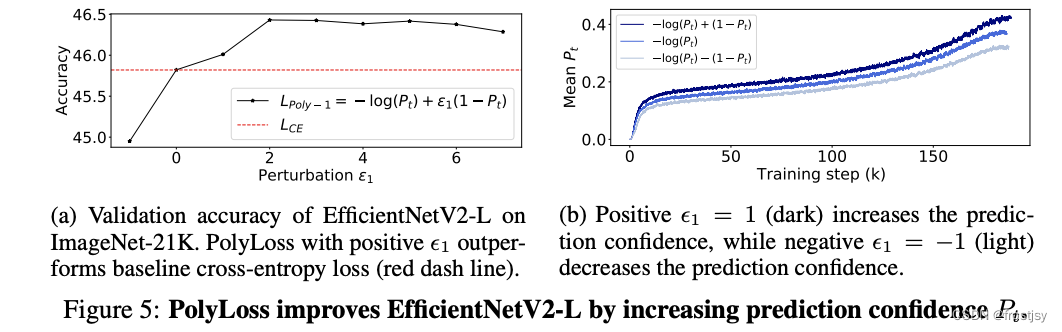
=2时趋于平缓,
为负时,会出现负项的效果。
4.2.2、提升效果对比
accurcy

4.3、COCO 上的 2D 实例分割和目标检测
4.3.1、AP/AR指标对比
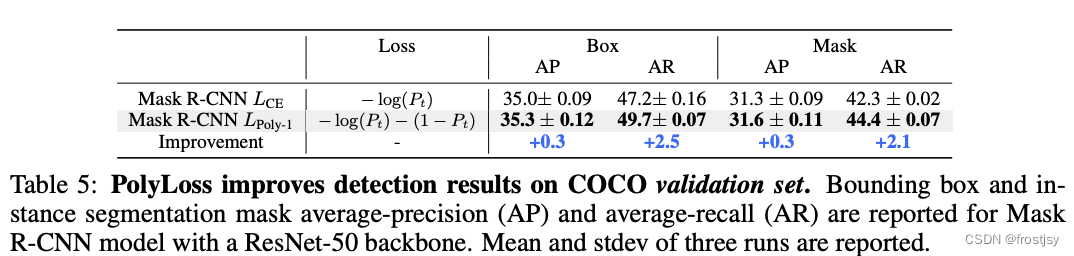
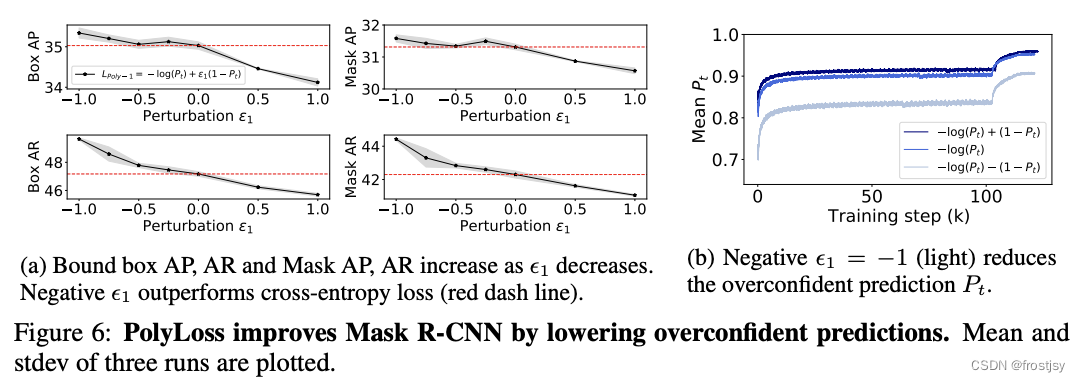
=-1时,效果提升显著
4.3.2、AP/AR指标对比
r-cnn通过降低来提高效果,
取负数时,效果优于正常的cross-entropy
4.4、3-d目标检查中,polyloss的设计及效果
4.4.1、loss设计

4.4.2、效果比较
车辆检测和行人检测效果不同polyloss效果对比
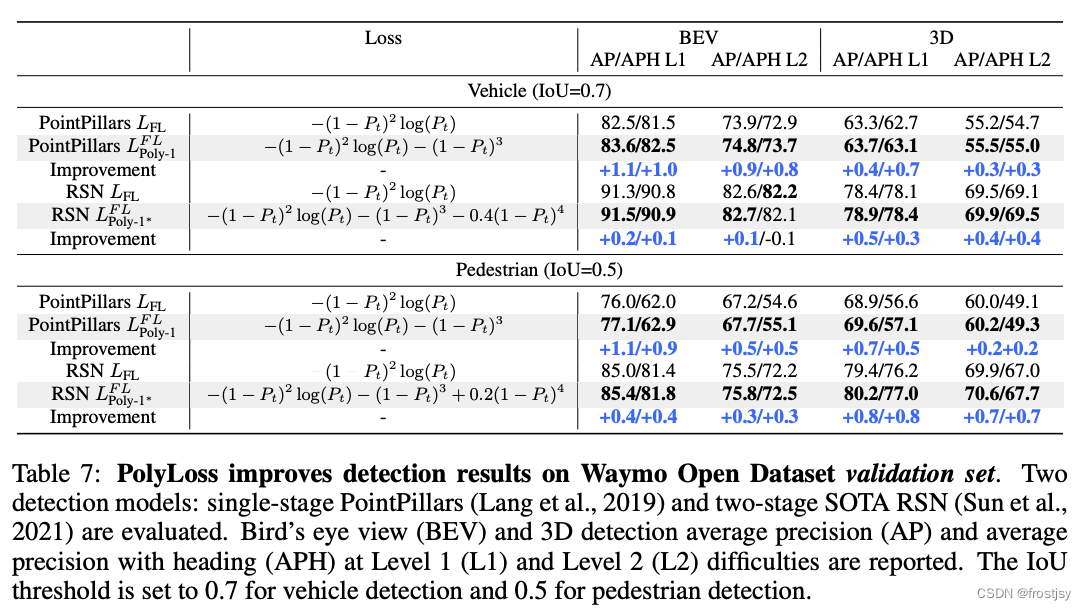
4.4.3、focal loss polyloss框架表示可视化如下
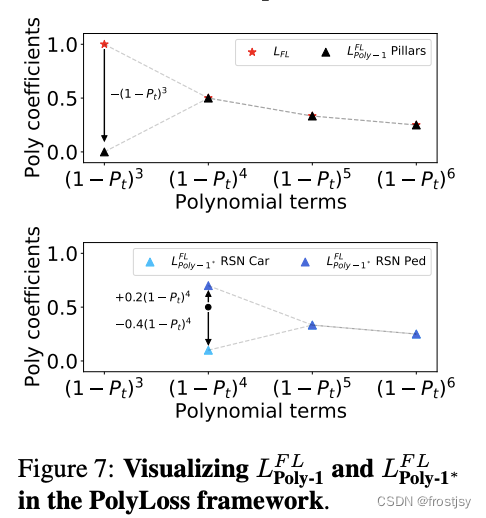
5、polyloss实现
def cross_entropy_tf(logits, labels, class_number):"""TF交叉熵损失函数"""labels = tf.one_hot(labels, class_number)ce_loss = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits)return ce_lossdef poly1_cross_entropy_tf(logits, labels, class_number, epsilon=1.0):"""poly_loss针对交叉熵损失函数优化,使用增加第一个多项式系数"""labels = tf.one_hot(labels, class_number)ce_loss = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits)poly1 = tf.reduce_sum(labels * tf.nn.softmax(logits), axis=-1)poly1_loss = ce_loss + epsilon * (1 - poly1)return poly1_lossdef focal_loss_tf(logits, labels, class_number, alpha=0.25, gamma=2.0, epsilon=1.e-7):"""TF focal_loss函数"""alpha = tf.constant(alpha, dtype=tf.float32)y_true = tf.one_hot(0, class_number)alpha = y_true * alpha + (tf.ones_like(y_true) - y_true) * (1 - alpha)labels = tf.cast(labels, dtype=tf.int32)logits = tf.cast(logits, tf.float32)softmax = tf.reshape(tf.nn.softmax(logits), [-1])labels_shift = tf.range(0, logits.shape[0]) * logits.shape[1] + labelsprob = tf.gather(softmax, labels_shift)prob = tf.clip_by_value(prob, epsilon, 1. - epsilon)alpha_choice = tf.gather(alpha, labels)weight = tf.pow(tf.subtract(1., prob), gamma)weight = tf.multiply(alpha_choice, weight)fc_loss = -tf.multiply(weight, tf.log(prob))return fc_lossdef poly1_focal_loss_tf(logits, labels, class_number=3, alpha=0.25, gamma=2.0, epsilon=1.0):fc_loss = focal_loss_tf(logits, labels, class_number, alpha, gamma)p = tf.math.sigmoid(logits)labels = tf.one_hot(labels, class_number)poly1 = labels * p + (1 - labels) * (1 - p)poly1_loss = fc_loss + tf.reduce_mean(epsilon * tf.math.pow(1 - poly1, 2 + 1), axis=-1)return poly1_loss6、polyone_cross_entory 拆解看
cross_entory计算调用tf.nn.softmax_cross_entropy_with_logits_v2,具体步骤如下:
- 首先,对
logits进行 softmax 归一化,得到预测的概率分布softmax_logits。- softmax 函数的计算公式:
softmax(x) = exp(x) / reduce_sum(exp(x), axis) - 其中,
exp(x)是指数函数,reduce_sum是对指数函数结果按指定轴求和。 - 归一化后的结果
softmax_logits的形状与logits相同,都是(N, C)。
- softmax 函数的计算公式:
- 接下来,根据
labels和softmax_logits计算交叉熵损失。- 交叉熵损失的计算公式:
loss = -reduce_sum(labels * log(softmax_logits), axis) - 其中,
log是自然对数函数,reduce_sum是对元素按指定轴求和。 - 最终的损失
loss的形状是(N,),其中每个元素表示对应样本的损失。
- 交叉熵损失的计算公式:
cross entory的poly-one展开项计算如下:
pt = tf.reduce_sum(labels_for_softmax * tf.nn.softmax(logits_for_softmax), axis=-1)
ce = tf.compat.v1.nn.softmax_cross_entropy_with_logits_v2(labels_for_softmax,logits_for_softmax)
losses = ce + self._epsilon * (1 - pt)pt与ce分别计算结果
labels = tf.constant([[0.0, 0.0, 1.0], [1.0, 0.0, 0.0]])
logits = tf.constant([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
loss1 = tf.compat.v1.nn.softmax_cross_entropy_with_logits_v2(labels, logits)
softmax_logits = tf.nn.softmax(logits)
loss2 = tf.reduce_sum(labels * softmax_logits, axis=-1)
loss1与loss2分别输出
#loss1输出
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([0.40760595, 2.407606 ], dtype=float32)>
#loss2输出
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([0.66524094, 0.09003057], dtype=float32)>参考网址
https://zhuanlan.zhihu.com/p/510626670
【Python-Tensorflow】tf.nn.softmax_cross_entropy_with_logits_v2()解析与使用-CSDN博客
高等数学(九)泰勒展开式 - 知乎
lnx的泰勒展开式该怎么写? - 知乎
https://blog.csdn.net/dawnyi_yang/article/details/124634171
Focal loss论文详解 - 知乎
https://arxiv.org/pdf/2204.12511.pdf
物体检测评估指标简介(AP和AR) - 简书