---

前言

本文讲解了基于 OFDM 的通信系统模拟实现。

---

一、OFDM 基本知识

1、OFDM 理论知识及仿真

有关 OFDM 相关理论知识及仿真参考我之前写过的博客：OFDM原理及MATLAB仿真

2、OFDM 调制

IDFT、IFFT

3、OFDM 解调

DFT、FFT

二、2ASK（二进制振幅键控）

因后面 OFDM 载波调制时每个子载波使用 2ASK 调制，因此这里对 2ASK 进行一个理论的讲解

1、2ASK 基本原理

振幅键控是利用载波的幅度变化来传递数字信息，而其频率和初始相位保持不变。在 2ASK 中，载波的幅只有两种变化状态，分别对应二进制信息 “0” 或 “1”。

①、OOK

一种常用的、也是最简单的二进制振幅键控方式称为通一断键控（OOK），其表达式为：
$$e_{OOK}(t)=\{\begin{array}{ll}Acos{\omega }_{c}t& \text{以概率 P 发送 “1” 时}\\ 0& \text{以概率 1-P 发送 “0” 时}\end{array}$$

典型波形如下图所示：

2ASK/OOK信号时间波形

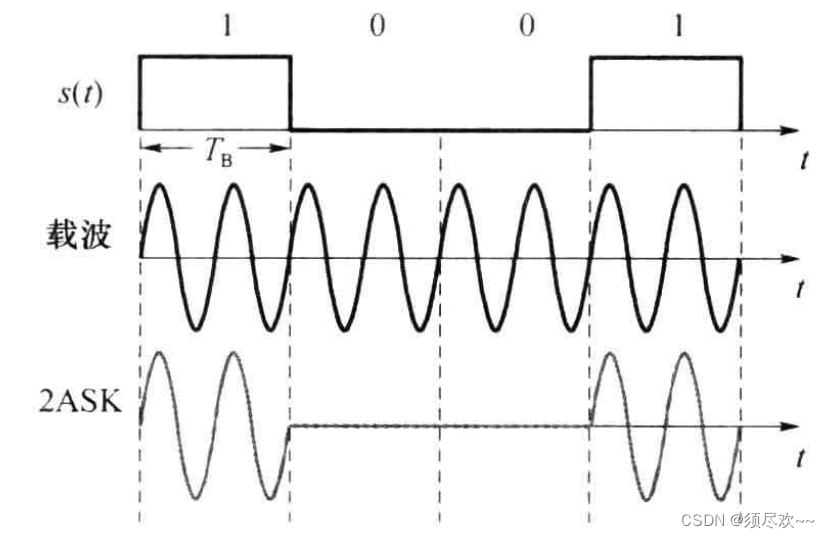
可见，载波在二进制基带信号 $s(t)$ 控制下通一断变化，所以这种键控又称为通一断键控。在 OOK 中，某一种符号（“0” 或 “1”）用有没有电压来表示

②、2ASK

2ASK 信号的一般表达式为：
$$e_{2ASK}(t)=s(t)cos{\omega }_{c}t$$
其中
$$s(t)=\sum _n{a}_{n}g(t-n{T}_B)$$
式中：$T_B$ 为码元持续时间；$g(t)$ 为持续时间为 $T_B$ 的基带脉冲波形。为简便起见，通常假设 $g(t)$ 是高度为 1、宽度等于 $T_B$ 的矩形脉冲；$a_n$ 是第 $n$ 个符号的电平取值。若取
$$a_n=\{\begin{array}{ll}1& \text{概率为 P}\\ 0& \text{概率为 1-P}\end{array}$$
则相应的 2ASK 信号就是 OOK 信号

2、2ASK/OOK 信号产生方法

2ASK/OOK 信号的产生方法通常有两种：模拟调制法（相乘器法）和键控法，相应的调制器如下图所示。图（a）就是一般的模拟幅度调制的方法，用乘法器（multiplier）实现；图（b）是一种数字键控法，其中的开关电路 $s(t)$控制

2ASK/OOK信号调制器原理框图

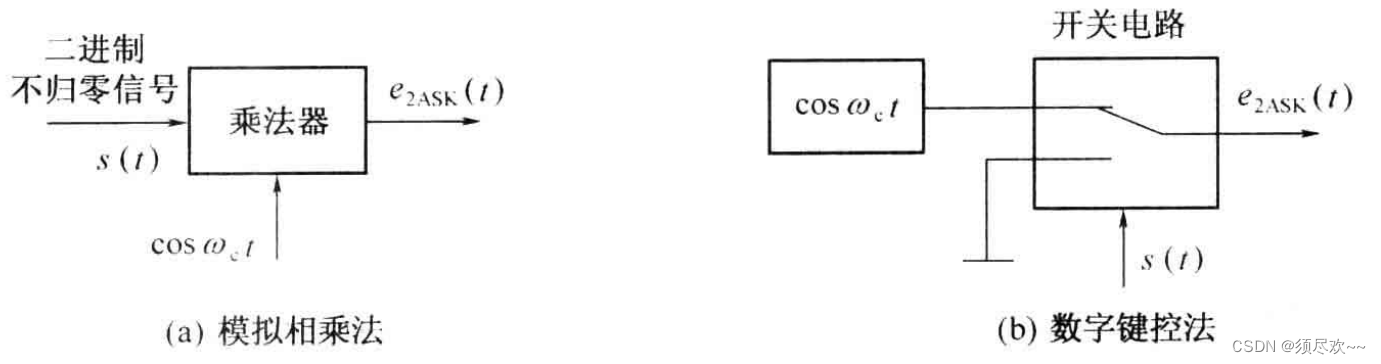
3、2ASK/OOK 信号解调方法

与 AM 信号的解调方法翌阳。2ASK/OOK 信号也有两种基本的解调方法：非相干解调（包络检波法） 和 相干解调（同步检测法），相应的接收系统组成方框图如下图所示：

2ASK/OOK信号的接收系统组成方框图

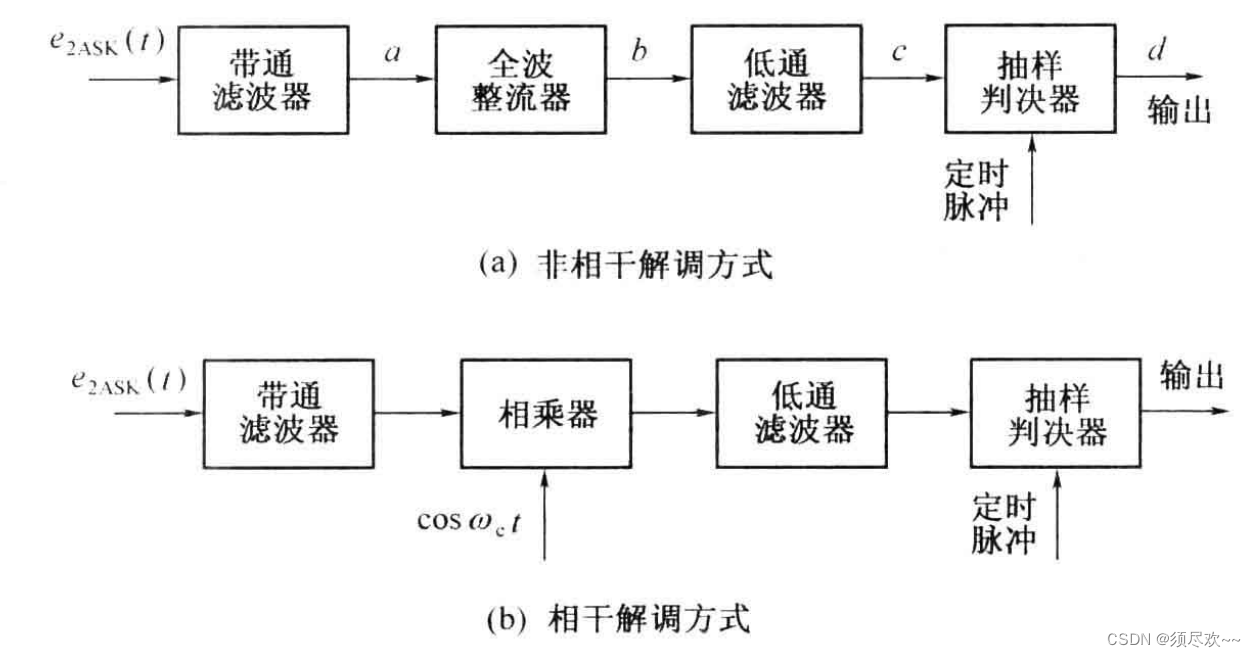
与模拟信号的接收系统相比，这里增加了一个“抽样判决器”方框，这对于提高数字信号的接收性能是必要的。

下图给出了 2ASK/OOK 信号非相干解调过程的时间波形

2ASK/OOK信号非相干解调过程的时间波形

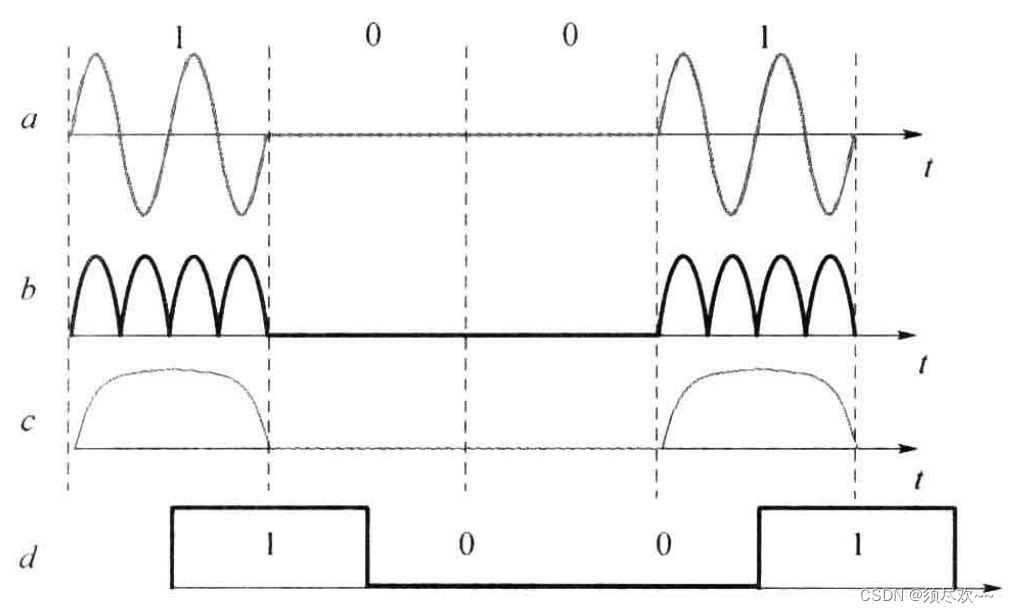
2ASK 是 20 世纪初最早运用于无线电报中的数字调制方式之一。但是，ASK 传输技术受噪声影响很大。噪声电压和信号一起改变了振幅。在这种情况下，“0” 可能变为 “1”，“1” 可能变为“0”。可以想象，对于主要依赖振幅来识别比特的 ASK 调制方法，噪声是一个很大的问题。由于 ASK 是受噪声影响最大的调制技术，现已较少应用，不过，2ASK 常常作为研究其他数字调制的基础，还是有必要了解它。

三、基于 OFDM 的通信系统模拟实现

1、整体流程

基于 OFDM 的通信系统模拟实现的整体流程图大致如下图所示：

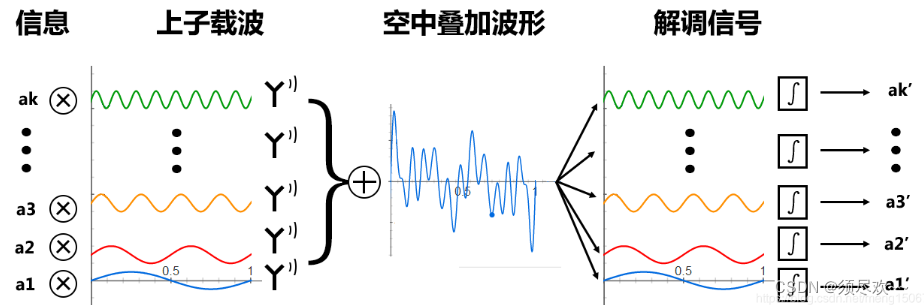
2、MATLAB 源码

% 这段代码是一个基于正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）
% 的通信系统的模拟实现。下面是对代码进行详细分析的解释：% 这些命令用于清除命令窗口、清除工作区变量和关闭所有打开的图形窗口
clc;            % 清除命令窗口
clear;          % 清除工作区变量
close all;      % 关闭所有打开的图形窗口% ===============================变量参数定义=============================================% 接下来的几行代码定义了一些变量和参数
M  = 8;			% 子载波数，指定了OFDM系统中的子载波数量
fc   = 1e6;		% 主载波频率/Hz，表示OFDM系统中的主载波频率
fsub = 1e3;		% 子载波频率间隔，表示相邻子载波之间的频率间隔
fsig = fc:fsub:fc+(M-1)*fsub; % 频率序列，计算出每个子载波的频率% 下面的几行代码定义了一些与时间和采样相关的参数
T  = 0.001;		% 子载波持续时间，表示每个子载波的时间长度
fs = 10e6;		% 采样频率/Hz，表示对信号进行采样的频率
ts = 1/fs;		% 采样时间间隔，表示相邻采样点之间的时间间隔
t  = 0:ts:T-ts;	% 一个符号周期的时间矢量，生成了一个从0到T的时间向量，用于表示一个符号周期内的时间% =============================== OFDM 频谱分析=============================================% 接下来的代码段生成了子载波信号，并进行了频谱分析
c  = zeros(M,length(t));% c 是一个大小为 M×length(t)(目前这里是8*10000) 的矩阵，用于存储 M 个子载波的信号
NN = length(t)*16;      % 计算了扩展后的采样点数，乘以 16 是为了提高频谱计算的分辨率，NN=10000*16
XN = zeros(M,NN);       % XN 是一个大小为 M×NN （目前这里是8*160000）的矩阵，用于存储每个子载波信号的频域表示
f0 = fs/NN;             % 采样间隔 = 采样率 / 采样点数
f  = (0:NN-1)*f0;       % 采样间隔序列，计算出每个采样间隔的开始频率
for k = 1:Mc(k,:)  = exp(1j*2*pi*fsig(k)*t);   % 生成一个复指数形式的子载波信号，通过循环遍历每个复指数形式的子载波，将复指数形式的子载波信号存储在矩阵 c 中XN(k,:) = fft(c(k,:),NN);           % 并对每个子载波的信号进行快速傅里叶变换（FFT）得到其频域表示，并将结果存储在矩阵 XN 中
end% 最后，使用 plot 函数将每个子载波的频谱绘制在一张图上，并设置图像的标题、坐标轴标签和图例。
figure;
plot(f,abs(XN(1,:)), f,abs(XN(2,:)), f,abs(XN(3,:)), f,abs(XN(4,:)), f,abs(XN(5,:)), f,abs(XN(6,:)), f,abs(XN(7,:)), f,abs(XN(8,:)));
legend('1000kHz子载波', '1001kHz子载波', '1002kHz子载波', '1003kHz子载波', '1004kHz子载波', '1005kHz子载波', '1006kHz子载波', '1007kHz子载波');
axis([995e3 1012e3 -inf inf]);  % x 轴范围设置成[995000，1012000]，y 轴范围最小值和最大值都为无穷
title('频域中 子载波分布图');
ylabel('幅度');
xlabel('频率/Hz');% =============================== OFDM 载波调制=============================================% OFDM载波调制（这里每个子载波使用 2-ASK 调制，实际上每个子载波使用PSK、QAM调制也可以）
symbol = M;                         % 定义了发送的符号数，这里与子载波数相等
msg  = randi([0 1],1,symbol);       % 并行发送 8bit 数据
% msg  = [1 1 0 1 1 1 0 1];         % 并行发送 8bit 数据
tx = zeros(1,length(t));            % tx 的大小是 1*10000，用来存储发射信号
for k = 1:length(msg)               % 通过循环遍历每个子载波，将每个子载波信号乘以对应的数据位（0或1），并将它们叠加得到最终的发送信号tx = tx + msg(k)*c(k,:);        % 子载波叠加
end
XN_tx = fft(tx,NN);                 % 使用FFT对发送信号 tx 进行频谱分析，并将结果存储在 XN_tx 中
disp(['发送数据： ' num2str(msg)]);  % 显示发送的数据 msg% =============================== OFDM 空中信道传输=============================================% 空中信道传输
sigma = sum(abs(tx))/length(tx) * 0.9;  % sigma 是根据发送信号 tx 的幅度计算得到的噪声标准差
rx    = tx + sigma*rand(1,length(tx));  % rx 是将发送信号 tx 加上高斯白噪声（AWGN）后得到的接收信号，加入AWGN（实际上只影响直流分量）
XN_rx = fft(rx,NN);                     % 使用FFT对接收信号 rx 进行频谱分析，并将结果存储在 XN_rx 中% =============================== OFDM 解调=============================================% OFDM解调
msg_demodulation = zeros(1,symbol);         % msg_demodulation 是一个大小为 1×symbol 的向量，用于存储解调后的数据
for k = 1:symbol                            % 通过循环遍历每个符号，利用FFT结果进行解调。如果接收到的信号在对应子载波的频谱中的幅度大于阈值（5e3），则将解调后的数据位设置为1，否则为0。if(abs(XN_rx(16001 + 16*(k-1))) > 5e3)  % 使用FFT结果来解调msg_demodulation(1,k) = 1;end
end
disp(['收到数据： ' num2str(msg_demodulation)]);bit_error_cnt = 0;                              % bit_error_cnt 用于存储比特错误的数量，初始值为0。
for k = 1:symbolif(msg_demodulation(k) ~= msg(k))           % 如果解调后的数据位与发送的数据位不一致% 当判定的接收比特与发送比特不一致时，认为判定错误bit_error_cnt = bit_error_cnt + 1;end
end
bit_error_percent = bit_error_cnt/symbol;       % 计算误码率 bit_error_percent，即比特错误的数量除以总的符号数。
disp(['误码率： ' num2str(bit_error_percent)]);figure;
subplot(2,1,1);plot(t,real(tx));axis([-inf inf -inf inf]);title('OFDM发送信号 时域图');
ylabel('幅度');
xlabel('时间/s');
subplot(2,1,2);plot(t,real(rx));axis([-inf inf -inf inf]);title('OFDM接收信号 时域图');
ylabel('幅度');
xlabel('时间/s');figure;
subplot(2,1,1);plot(f,abs(XN_tx));axis([995e3 1012e3 -inf inf]);title('OFDM发送信号 频谱');
ylabel('幅度');
xlabel('频率/Hz');
subplot(2,1,2);plot(f,abs(XN_rx));axis([995e3 1012e3 -inf inf]);title('OFDM接收信号 频谱');
ylabel('幅度');
xlabel('频率/Hz');

3、仿真结果

①、OFDM 频谱分析

OFDM 频谱分析

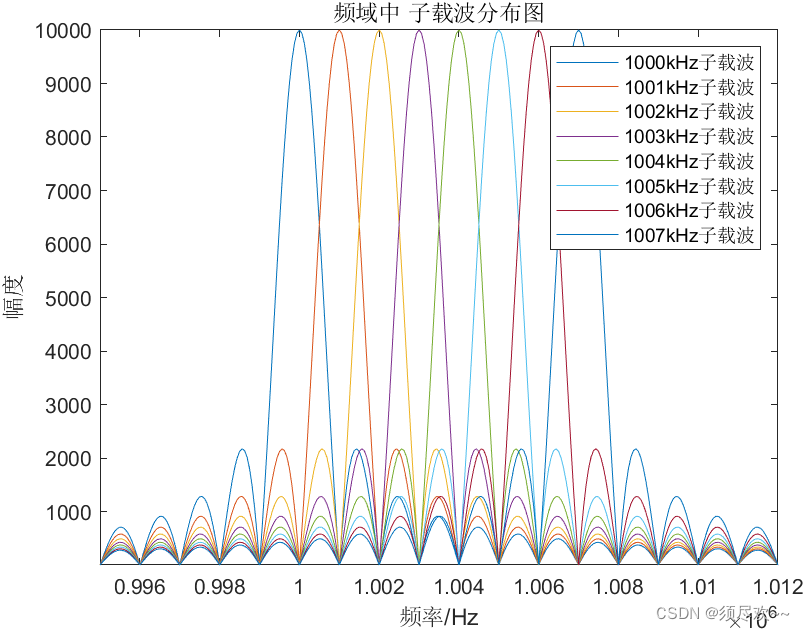
②、OFDM 发送及接收信号时域图

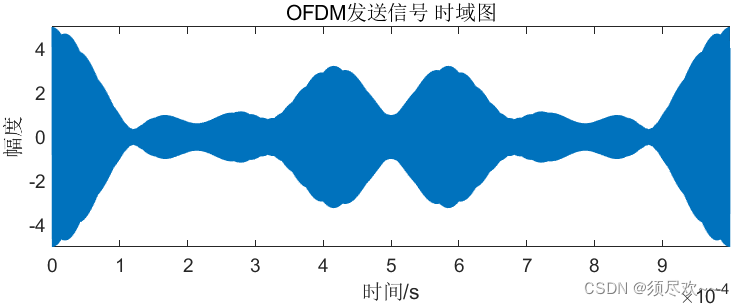
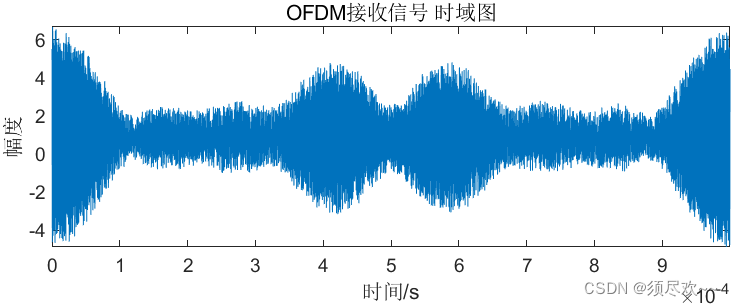
③、OFDM 发送及接收信号频谱图

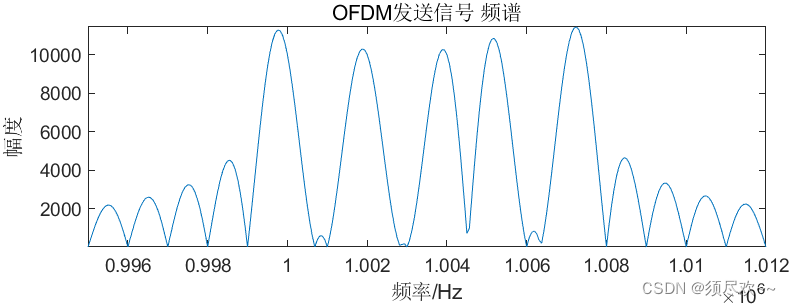
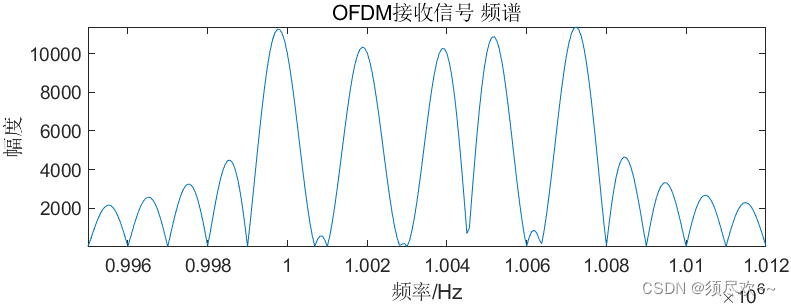
④、OFDM 误码率

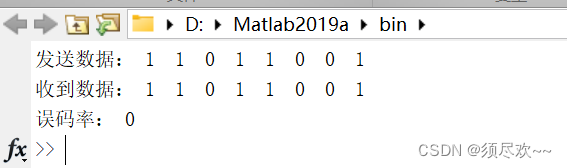
四、资源自取

基于OFDM的通信系统模拟实现

---

我的qq：2442391036，欢迎交流！

---