Leetcode 542. 01 矩阵

542. 01 矩阵-中等

问题描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：
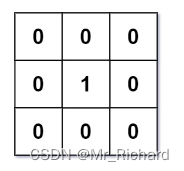
在这里插入图片描述

输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

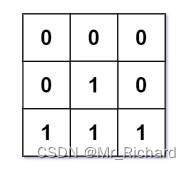
在这里插入图片描述

输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0

解题思路与代码实现一

采用BFS搜索解题：

创建标记数组visited用于标记已访问过的元素，初始化均为Integer.MAX_VALUE（不小于可能的最大步长m+n-1），因为在BFS的过程中，先被访问的元素的步长一定小于等于后被访问的元素；创建队列queue用于实现BFS，初始化均为false；
扫描mat数组，需要把所有mat[i][j]为0的元素加入队列并标记为已访问；
接着扫描队列，当队列不为空时，队头元素出队，依次访问其上下左右的周围点，如果未发生数组越界且该周围点没被访问过，则将其入队并标记为已访问（true），同时更新周围点的步长 = 出队元素的步长 +1；

public int[][] updateMatrix2(int[][] mat) {// m、n分别表示矩阵的行数和列数int m = mat.length, n = mat[0].length;// 依次表示 上、左、下、右周围四个点的偏移量int[][] dirs = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};// BFS用的队列Queue<int[]> queue = new LinkedList<>();// 标记数组boolean[][] visited = new boolean[m][n];for (int i = 0; i < m; i++) {// 标记数组初始化全为false，mat[i][j]为0的元素会被标记为trueArrays.fill(visited[i], false);for (int j = 0; j < n; j++) {if (mat[i][j] == 0) {// mat[j][j]为0的元素标记为true并优先入队visited[i][j] = true;queue.offer(new int[]{i, j});} else {mat[i][j] = Integer.MAX_VALUE;}}}while (!queue.isEmpty()) {// 从队列中取出访问过的一个元素作为当前点，访问其周围点int[] current = queue.poll();int currentX = current[0];int currentY = current[1];for (int[] dir : dirs) {// 依次表示 上、左、下、右周围四个点的x、y坐标int x = currentX + dir[0];int y = currentY + dir[1];// 如果坐标未越界，且该周围点mat[x][y]未被访问过（由BFS概念可知，先被访问的的mat[i][j]一定不会超过后访问的）// 也可以不使用标记数组，替换为判断 不越界 且 当前点的距离小于周围点(mat[currentX][currentY] < mat[x][y])，但效率却更低些if (x >= 0 && x < m && y >= 0 && y < n && !visited[x][y]) {// 标记访问过，并入队visited[x][y] = true;queue.offer(new int[]{x, y});// 更新值mat[x][y] = mat[currentX][currentY] + 1;}}}return mat;
}

解题思路与代码实现二

采用动态规划：

先找最优子结构，很明显，一个点的最短距离应该是它周围上下左右四个点（如果存在的话）的最短距离+1，即：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

dp[i][j]表示（i，j)到0的最短距离，但由于0所在位置不固定，所以先将dp数组初始化：mat[i][j]为0，则dp[i][j]取0，否则dp[i][j]取20000（最长距离：m+n-1=19999<20000）。然后为分两轮进行比较：

第一轮从左到右从上到下扫描mat数组，dp[i][j]取mat[i-1][j]+1、mat[i][j-1]+1和dp[i][j]的最小值，需要注意下标越界；
第二轮从右到左从下到上扫描mat数组，dp[i][j]取mat[i][j+1]+1、mat[i+1][j]+1和dp[i][j]的最小值，需要注意下标越界；

两轮扫描结束后，dp[i][j]表示（i，j)到0的最短距离，即为所求

		public int[][] updateMatrix(int[][] mat) {// m、n分别表示矩阵的行数和列数int m = mat.length, n = mat[0].length;// dp数组int[][] dp = new int[m][n];// dp数组初始化for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 19999为1 <= m, n <= 104条件下，可能出现的最大长度 m + n -1dp[i][j] = mat[i][j] == 0 ? 0 : 20000;}}// 先更新左边和上边的最小值for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 判断上边是否越界if (i - 1 >= 0) {dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j]);}// 判断左边是否越界if (j - 1 >= 0) {dp[i][j] = Math.min(dp[i][j - 1] + 1, dp[i][j]);}}}// 再更新右边和下边的最小值for (int i = m - 1; i >= 0; i--) {for (int j = n - 1; j >= 0; j--) {if (i + 1 < m) {dp[i][j] = Math.min(dp[i + 1][j] + 1, dp[i][j]);}if (j + 1 < n) {dp[i][j] = Math.min(dp[i][j + 1] + 1, dp[i][j]);}}}return dp;}