一、双链表

（一）双链表的定义

双链表是在单链表结点上增添了一个指针域prior，指针域prior指向当前结点的前驱结点，即此时链表的每个结点中都有两个指针域prior和next，从而可以很容易通过后继结点找到前驱结点，故访问前驱和后继结点的时间复杂度都为O(1)。

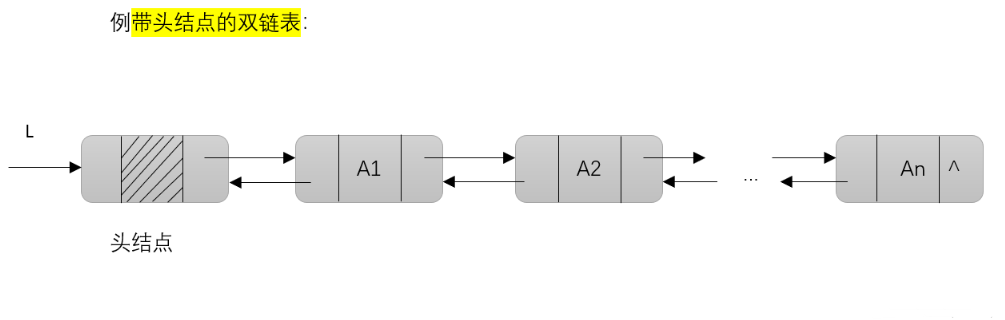
（二）双链表的判空

一个带头结点L的双链表，若L->next==NULL时，则该双链表为空；一个不带头结点的双链表，若L==NULL时，则该双链表为空。

双链表	判空条件
带头结点	L->next==NULL
不带头结点	L==NULL

（三）双链表的插入操作

• 由于双链表可以很快地找到前驱结点，所以双链表的插入、删除操作的时间复杂度都为O(1)。

双链表的插入操作可以概括为【先连后，后连前】，若在指针 *p 指向的结点之后插入结点 *q，首先，新结点q与原本 *p的指针域相连，即下一个结点，然后将结点q插入到结点p之后，再将其prior和next域相连，代码如下：

q->next=p->next;
p->next->prior=q;
q->prior=p;
p->next=q;

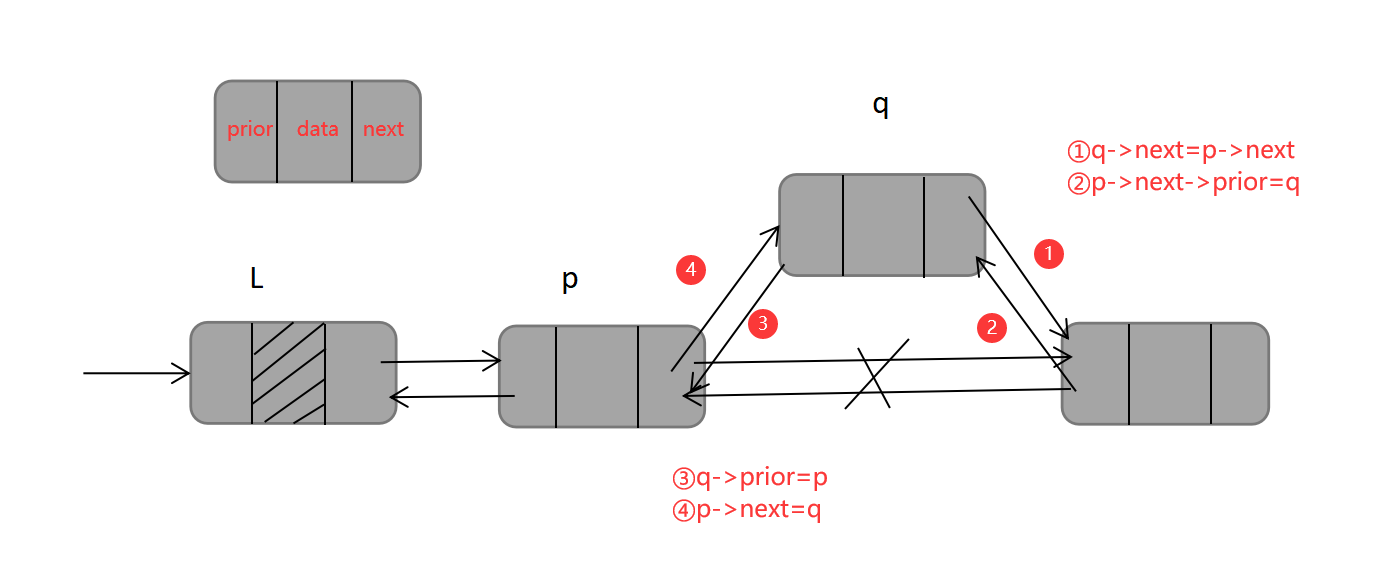
这里的代码插入不唯一，插入操作必须保证的是不能断链，即不能导致*p的后继结点的指针丢掉。

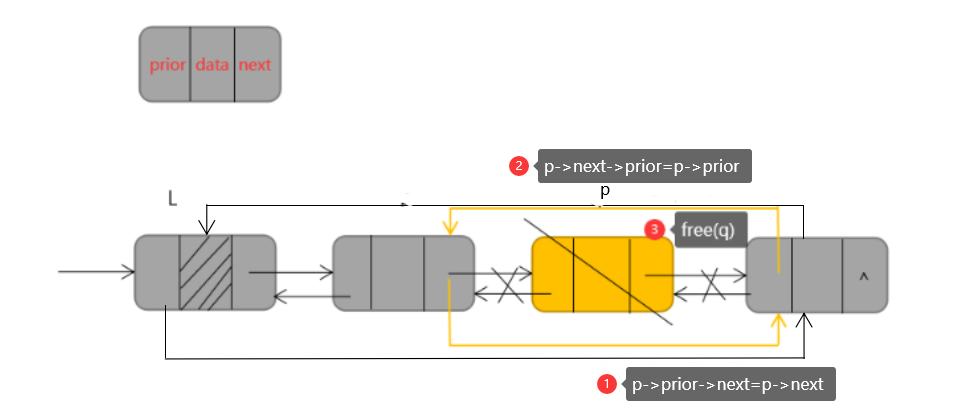
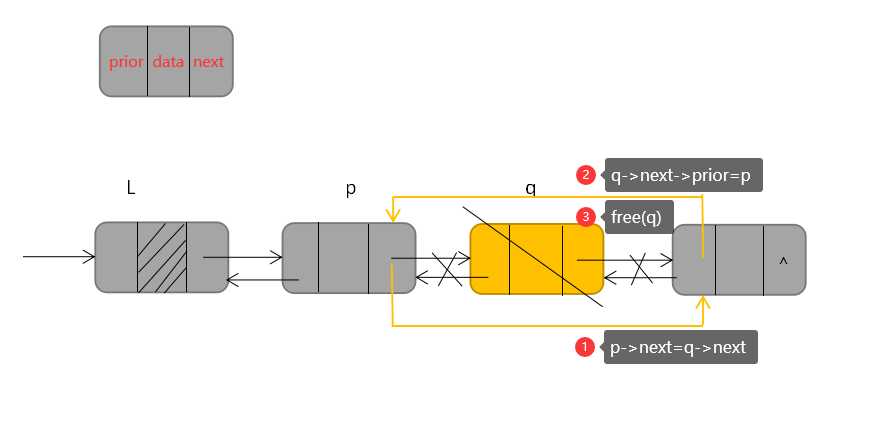
（四）双链表的删除操作

双链表的删除操作的代码如下：

p->next=q->next;
q->next->prior=p;
free(q);

二、循环单链表

（一）循环单链表的定义

循环单链表可以实现从任一个结点访问链表中的任何结点（遍历整个链表。

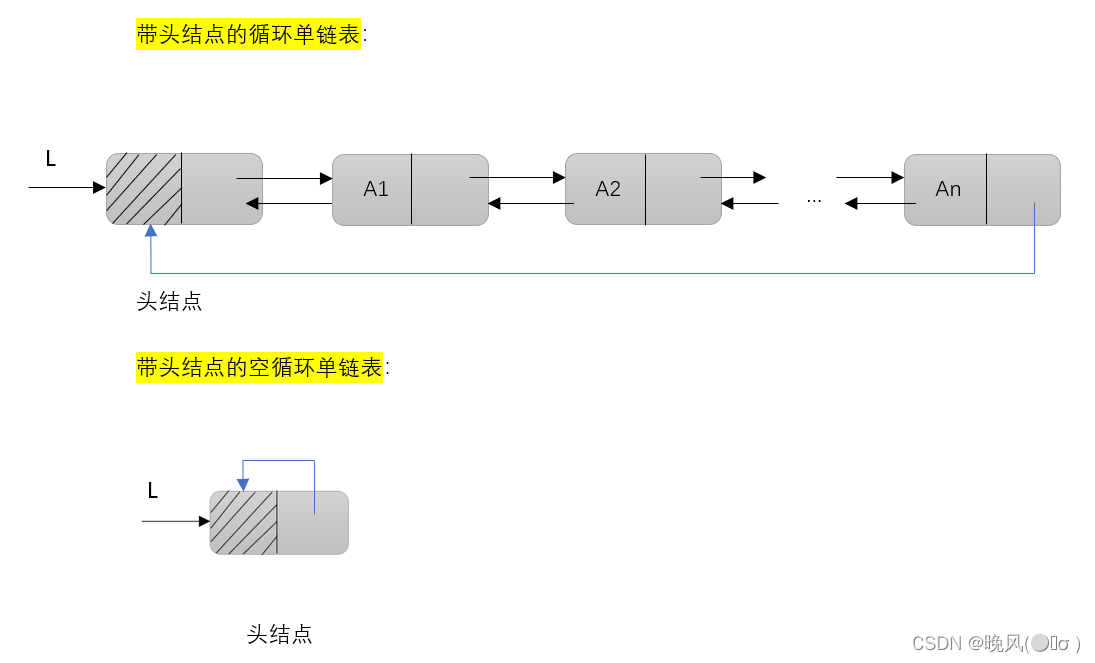
（二）循环单链表的判空

在带头结点L的循环单链表中，若L==head->next时，循环单链表为空；在不带头结点的循环单链表中，若L==NULL时，循环单链表为空。

循环单链表	判空条件
带头结点	L==head->next
不带头结点	L==NULL

（三）循环单链表的查找

在一个带头结点的循环单链表中：
1、若只设置头指针L，则查找表头结点的时间复杂度为O(1)，查找表尾结点需要依次遍历整个链表，即时间复杂度为O(n)，而查找一个结点的前驱结点时的时间复杂度为O(n)。
2、若只设置尾指针R，这样的好处是可以使查找链表的开始结点和终端结点很方便，其查找时间都为O(1)，而查找一个结点的前驱结点时的时间复杂度为O(n)。

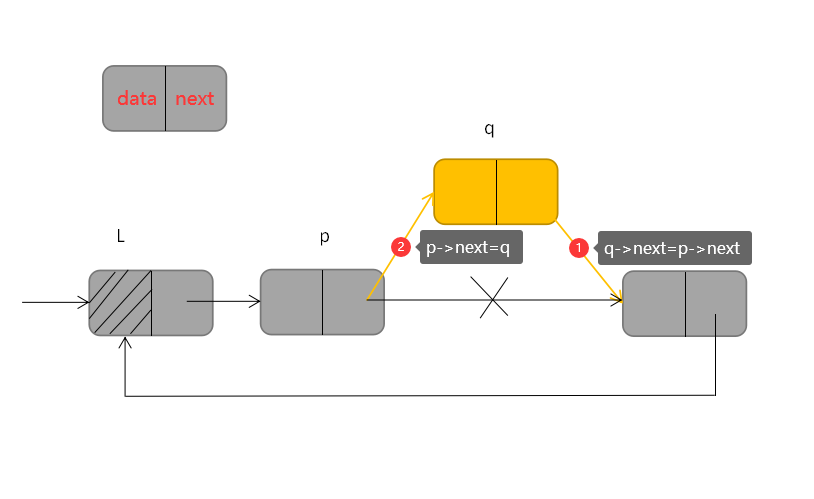
（四）循环单链表的插入操作

循环单链表的插入操作与单链表类似，也是【先连后，再连前】，若在指针 *p 指向的结点后插入结点 *p ，步骤是：首先将q的指针域与p结点原本的指向下一个结点的指针域相连，即q->next=p->next，然后再将q结点与p结点相连，即p->next=q，如下：

q->next=p->next;	//先连后
p->next=q;		//再连前

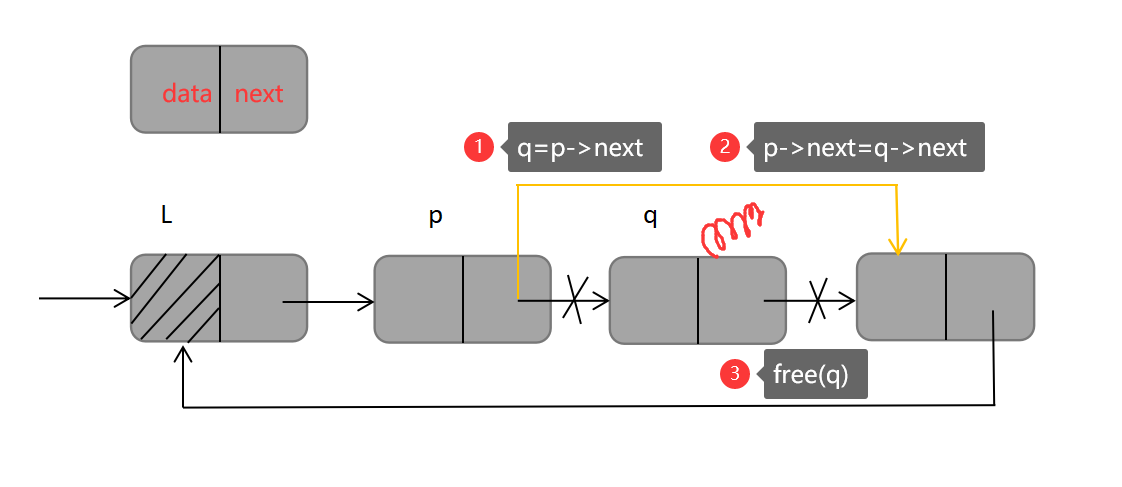
（五）循环单链表的删除操作

循环单链表的删除操作也与单链表类似，删除的步骤可概括为【先定位，后断开释放】，将*q指针指向要删除的结点，p为其前驱结点，如下代码：

q=p->next;	//先定位，定位删除位置
p->next=q->next;	//断开q与p的连接，p与下一个结点连接
free(q);	//free()函数释放结点

三、循环双链表

（一）循环双链表的定义

循环双链表基于双链表，头结点L的prior域指向表尾结点，查找表头结点和表尾结点的时间复杂度均为O(1)，查找一个结点的前驱结点时的时间复杂度也为O(1)。

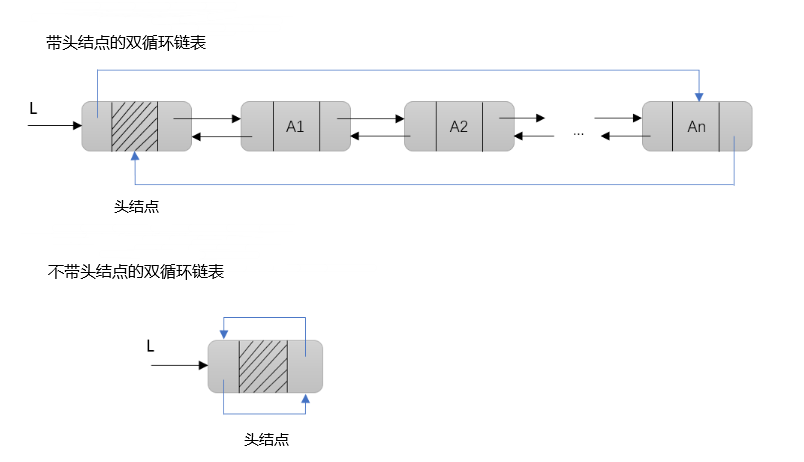
（二）循环双链表的判空

一个带头结点L的循环双链表，若L->prior==L&&L->next==L时，则该双链表为空。（头结点的prior和next域都指向其本身时为空）

循环双链表	判空条件
带头结点	L->prior == L && L->next == L
不带头结点	L==NULL

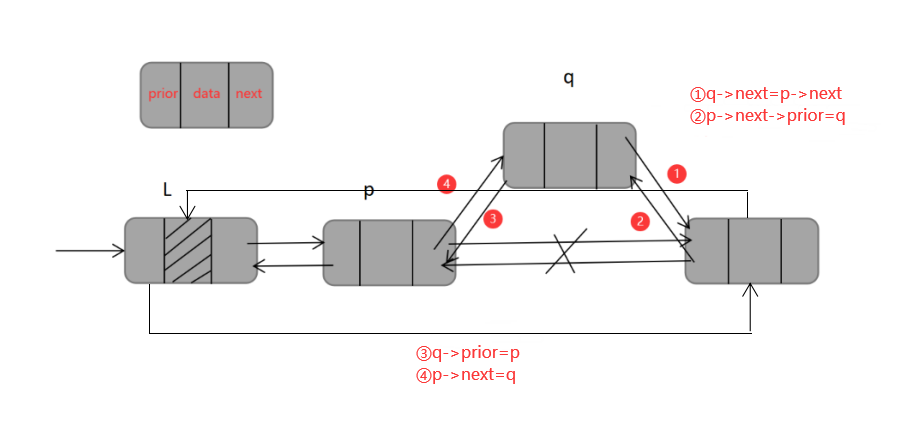
（三）循环双链表的插入操作

若要在指针 *p 指向的结点后插入结点 *p，其代码如下：

q->next=p->next;
p->next->prior=q;
q->prior=p;
p->next=q;

（四）循环双链表的删除操作

将*p指针指向要删除的结点，其代码如下：

p->next->prior=p->prior;
p->prior->next=p->next;
free(p);