堆排序是一种基于堆数据结构的排序算法,它的基本思想是将待排序序列构造成一个最大堆,然后将堆顶元素和堆底元素交换,再把堆的大小减一,使堆顶元素下沉到合适的位置,重复以上操作,直到整个序列有序。
堆排序分为两个基本操作:建堆和排序。建堆的过程是把无序序列构建成一个堆,这个过程从最后一个非叶子节点开始,依次将每个节点和其子节点构成一个小堆或大堆。排序的过程是将堆顶元素和堆底元素交换,然后把堆的大小减一,使堆顶元素下沉到合适的位置,重复直到堆的大小变为1为止,最终得到一个从小到大排序的序列。
堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)。它是一种不稳定的排序算法,但由于它的时间复杂度比较稳定,因此在大规模数据排序时表现优秀。
交换排序:堆排序(不稳定的排序)
堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆是一个完全二叉树,可以分为最大堆和最小堆两种。最大堆的每个父节点都比它的子节点大,而最小堆的每个父节点都比它的子节点小。
堆排序的基本思路是将待排序的元素构造成一个最大堆,此时整个序列的最大值就是堆顶的根节点。将它移走(其实就是将其与堆数组的末尾元素交换位置),然后将剩余的n-1个元素重新构造成一个堆,这样就会得到n个元素中的次小值。如此反复执行,便能得到一个有序的序列了。
堆排序的时间复杂度为O(nlogn),最坏情况下也是O(nlogn),空间复杂度为O(1)。但它的常数因子较大,实际使用时可能不如快速排序和归并排序。
大根堆 87,45,78,32,17,65,53,9 可以看成
87
45 78
32 17 65 53
9
也就相当于是完全二叉树



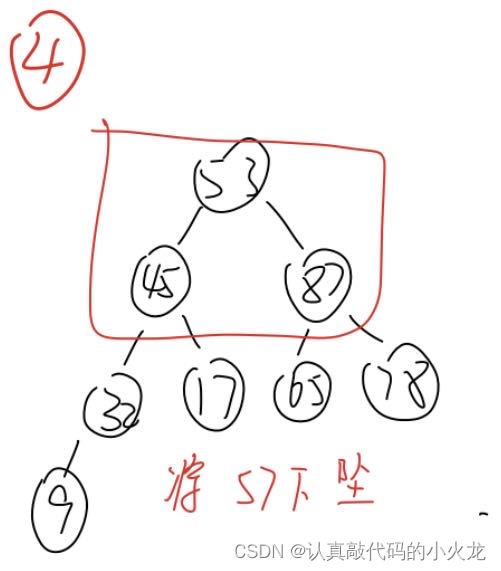
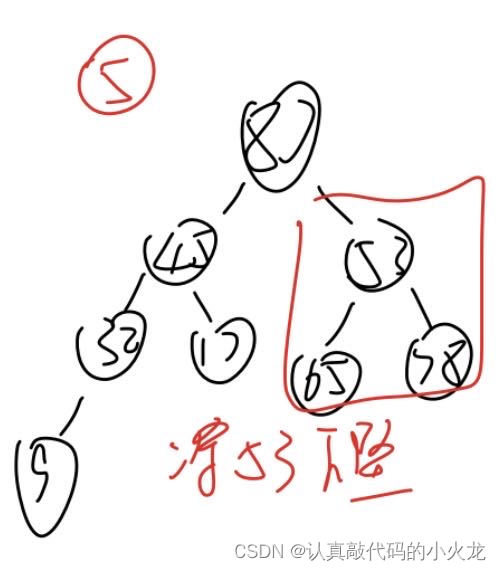
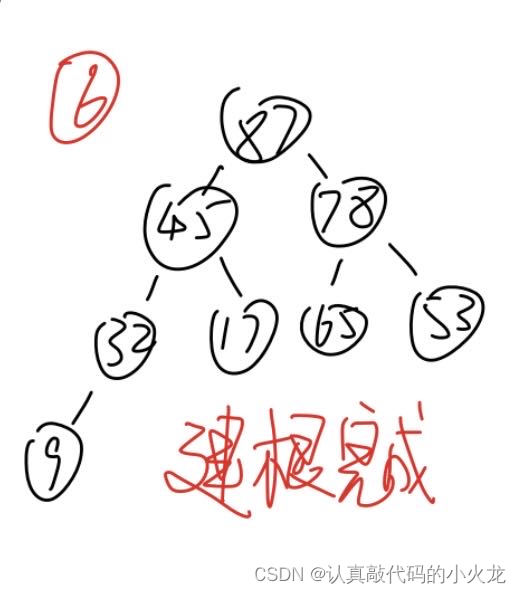
下面来看一下代码该如何实现
首先是主要思路
void heapsort(int a[], int sz)
{buildmaxheap(a, sz);//初始建堆int i = 0;int temp = 0;for (i = sz-1; i > 1; i--)//n-1趟的交换和建堆过程{temp = a[i];a[i] = a[1];a[1] = temp;headajust(a, 1, i - 1);//把剩余的i-1个元素调整成堆}
}建大根堆的代码是这样的👇
void buildmaxheap(int a[], int sz)
{int i = 0;for (i = sz / 2; i > 0; i--)//从i=a[sz/2]~1,反复调整堆headajust(a, i, sz);
}将元素传入以元素k为根的子树进行调整👇
void headajust(int a[], int k, int sz)
{int i = 0;a[0] = a[k];//暂存子树的根结点for (i = k * 2; i <= sz; i *= 2)//沿较大的子结点向下筛选{if (i < sz && a[i] < a[i + 1])//指向最大的孩子结点i++;if (a[0] >= a[i])break;else{a[k] = a[i];//将a[i]调整到双亲结点上k = i;//修改k的值,以便继续向下筛选}}a[k] = a[0];//被筛选的结点的值放入最终位置
}完整测试代码
#include<stdio.h>
void headajust(int a[], int k, int sz)
{int i = 0;a[0] = a[k];//暂存子树的根结点for (i = k * 2; i <= sz; i *= 2)//沿较大的子结点向下筛选{if (i < sz && a[i] < a[i + 1])//指向最大的孩子结点i++;if (a[0] >= a[i])break;else{a[k] = a[i];//将a[i]调整到双亲结点上k = i;//修改k的值,以便继续向下筛选}}a[k] = a[0];//被筛选的结点的值放入最终位置
}
void buildmaxheap(int a[], int sz)
{int i = 0;for (i = sz / 2; i > 0; i--)//从i=a[sz/2]~1,反复调整堆headajust(a, i, sz);
}
void heapsort(int a[], int sz)
{buildmaxheap(a, sz);//初始建堆int i = 0;int temp = 0;for (i = sz-1; i > 1; i--)//n-1趟的交换和建堆过程{temp = a[i];a[i] = a[1];a[1] = temp;headajust(a, 1, i - 1);//把剩余的i-1个元素调整成堆}
}
int main()
{int a[] = { 0,49,38,65,97,76,13,27 };int sz = sizeof(a) / sizeof(a[0]);int j = 0;printf("原始待排序的数组为:");for(j = 1; j < sz; j++)printf("%d ", a[j]);heapsort(a,sz);printf("\n堆排序后的数组为:");for (j = 1; j < sz; j++)printf("%d ", a[j]);return 0;
}