本文学习总结自：How to use the ACM SIGGRAPH / TOG LaTeX template
相关文件：百度网盘

---

首先解压 “my paper” 中的文件，并用Latex打开mypaper.tex.

多行连等公式

\begin{equation}表示编号公式，\[ \]表示无编号公式

1. 无编号

   \begin{align*}\Delta\left(v\right) &= \sum_{p\in planes(v)}{\left(v^Tp\right)\left(p^Tv\right)} \\&= \sum_{p\in planes(v)}{v^T\left(p^Tp\right)v} \\&= v^T\left(\sum_{p\in planes(v)}{K_p}\right)v
   \end{align*}
   

   实现结果：
   $$\begin{array}{rl}\Delta \left(v\right)& =\sum _{p\in planes(v)}\left(v^{T}p\right)\left(p^{T}v\right)\\ & =\sum _{p\in planes(v)}{v}^T\left(p^{T}p\right)v\\ & =v^T\left(\sum _{p\in planes(v)}{K}_p\right)v\end{array}$$
2. 有编号
   • 共同编号

     \begin{equation}\begin{aligned} %也可使用\begin{split}\Delta\left(v\right) &= \sum_{p\in planes(v)}{\left(v^Tp\right)\left(p^Tv\right)} \\&= \sum_{p\in planes(v)}{v^T\left(p^Tp\right)v} \\&= v^T\left(\sum_{p\in planes(v)}{K_p}\right)v\end{aligned} %\end{split}
     \end{equation}
     

     实现结果（其中aligned表示为多行公式，split表示整体为一个公式）：
     $$\begin{array}{c}\begin{array}{rl}\Delta \left(v\right)& =\sum _{p\in planes(v)}\left(v^{T}p\right)\left(p^{T}v\right)\\ & =\sum _{p\in planes(v)}{v}^T\left(p^{T}p\right)v\\ & =v^T\left(\sum _{p\in planes(v)}{K}_p\right)v\end{array}\end{array}$$
   • 单独编号

     \begin{align}\Delta\left(v\right) &= \sum_{p\in planes(v)}{\left(v^Tp\right)\left(p^Tv\right)} \\&= \sum_{p\in planes(v)}{v^T\left(p^Tp\right)v} \\&= v^T\left(\sum_{p\in planes(v)}{K_p}\right)v
     \end{align}
     

     实现结果（其中加入\nonumber会使本行不编号）：
     $$\begin{array}{rl}\Delta \left(v\right)& =\sum _{p\in planes(v)}\left(v^{T}p\right)\left(p^{T}v\right)\\ & =\sum _{p\in planes(v)}{v}^T\left(p^{T}p\right)v\\ & =v^T\left(\sum _{p\in planes(v)}{K}_p\right)v\end{array}$$

矩阵

\cdots表示横向多点$\cdots$，\vdots表示竖向多点 $⋮$，\ddots表示斜向多点$\ddots$

1. 矩阵表示

   \[K_p=pp^T=\left[\begin{array}{cccc}a^2 & ab & ac & ad \\ab & b^2 & bc & bd \\ac & bc & c^2 & cd \\ad & db & dc & d^2 \\\end{array}\right]
   \]
   

   实现结果（其中{cccc}代表有4列，若为方阵可直接使用\begin{matrix}）：
   $$K_p=p{p}^T=\left[\begin{array}{cccc}{a}^2& ab& ac& ad\\ ab& b^2& bc& bd\\ ac& bc& c^2& cd\\ ad& db& dc& d^2\end{array}\right]$$
2. 矩阵连乘

   \begin{equation}\left[\begin{array}{c}\varphi \\\theta \\\psi\end{array}\right]=\left[\begin{array}{ccc}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right]\left[\begin{array}{c}b_{1} \\ b_{2} \\b_{3}\end{array}\right]
   \end{equation}
   

   实现结果：
   $$\begin{array}{c}\left[\begin{array}{c}\phi \\ \theta \\ \psi \end{array}\right]=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]\end{array}$$

列表

1. 有序列表

   \begin{enumerate}\item $(v_1, v_2)$ is an edge, or\item $\lVert v_1 - v_2 \rVert < t$, where $t$ is a threshold parameter
   \end{enumerate}
   

   实现效果（默认为()，通过\item[1.]修改格式）：
   

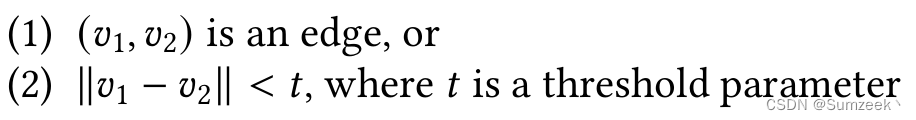
2. 无序列表

   \begin{itemize}\item $(v_1, v_2)$ is an edge, or\item $\lVert v_1 - v_2 \rVert < t$, where $t$ is a threshold parameter
   \end{itemize}
   

   实现效果（默认为·，通过\item[-]修改格式）：
   

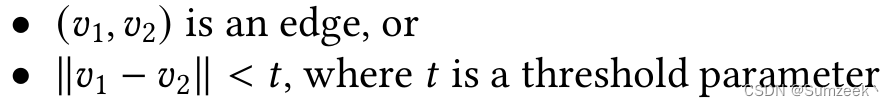
引用公式

需要在某个公式后添加\label{}标签

\ref{eq1}