一、题目解析
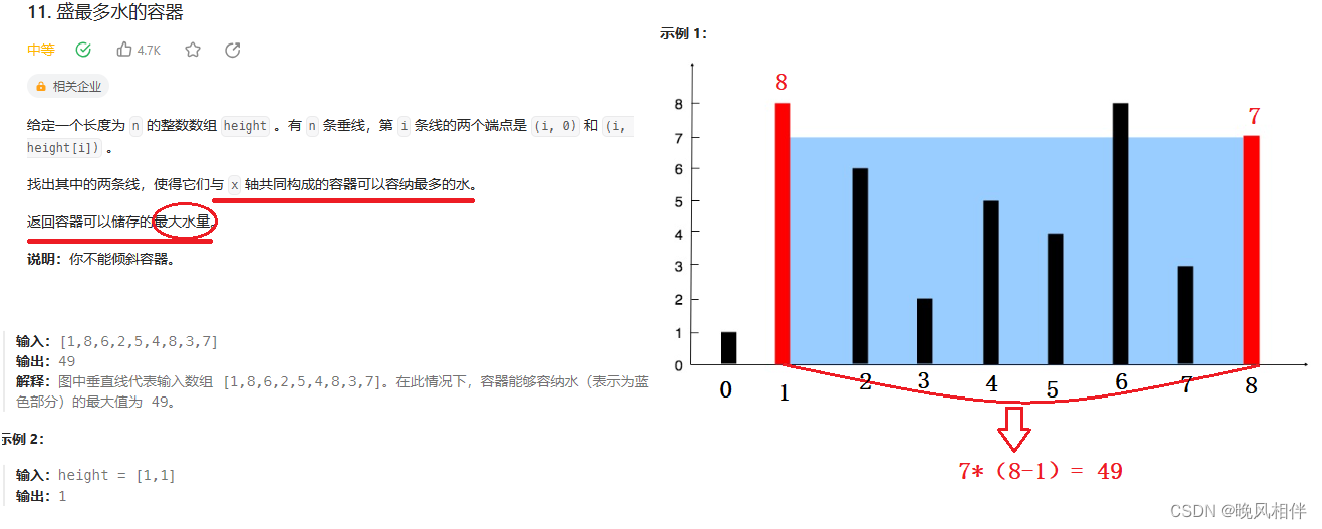
分析这个题目不难得出一个容积公式

二、算法原理
解法一:暴力枚举(超时)
套用上述的容积公式,使用两个for循环来枚举出所有可能的情况,再挑出最大值即可,但是这种写法会超时,导致不通过。时间复杂度是O(n^2)
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int ret = 0; for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {ret = max(ret, min(height[i], height[j]) * (j - i));}}return ret;}
};可以自己去尝试一下。
解法二:双指针
设两个指针left,right分别为这个容器的左边界和右边界,根据容积公式可得
v = min( height[right], height[left]) * (right - left)从题目中的测试用例中选取一段进行分析如下: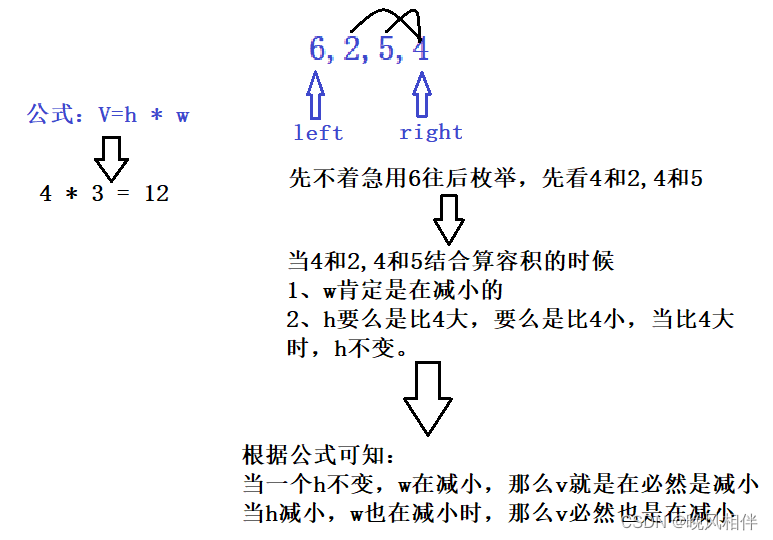
所以我们可以得出结论:用较小的数向内枚举的话容积肯定是在减小的,所以较小的数我们就可以不用向后枚举了直接跳过,用较大的数向后枚举就行。
最后选出容积最大值就行了。 时间复杂度是O(n)。
三、代码编写
class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, ret = 0;while(left < right){int v = min(height[left],height[right]) * (right - left);ret = max(ret, v);if(height[left] < height[right]){left++;}else {right--;}}return ret;}
};