343. 整数拆分
力扣题目链接
题目描述:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
思路:
- 思路就是把整数拆分成两数之和,三数以上可以不用管,因为三数以上其实就是两数拆分的,我们就用两个数来做题,分别取第一个数和第一个数的dp之间的最大值,以及第二个数和第二个数dp之间的最值,然后相乘就是当前组的最大值,最后不断循环和dp[i]比较取最值即可。
- 动态规划五部曲:
- 分析dp数组含义:dp[ i ]数组代表下标为i的整数拆分后元素乘积的的最大值
- 分析递推公式:
dp[i] = max(dp[i], max(dp[i - j], i - j) * max(dp[j], j)); - dp数组初始化:因为我们拆分是从1开始拆分的那么下标0可以不用管,把下标1赋值为1,2也赋值为1,因为2只能拆分为1+1.
- 遍历顺序:显然是从前往后遍历,我们遍历的时候从下标i = 3开始,内层循环是去拆分i,比如3从1开始拆分为1和2,但是这里上界其实到 i / 2就可以了,多了就重复了。
- 推导数组结果:
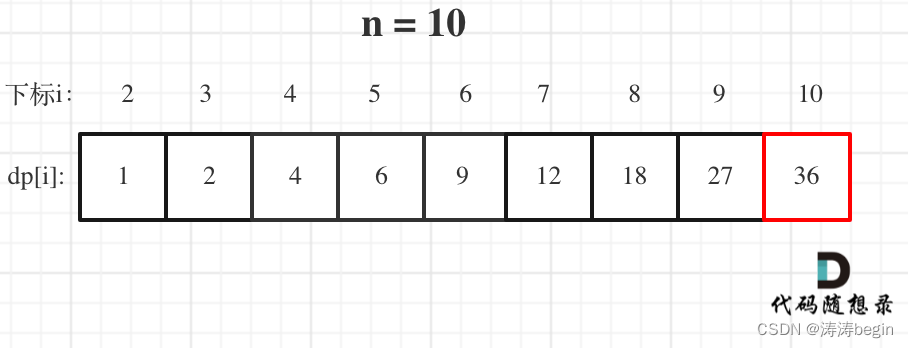
代码实现:
int integerBreak(int n) {/*dp[n] = max(dp[1]dp[n - 1],dp[2]dp[n - 2]..., dp[n / 2]dp[n - n / 2]);即:dp[i] = max(dp[i], max(dp[i - j], i - j) * max(dp[j], j));*/vector<int>dp(n + 1, 0);dp[1] = 1, dp[2] = 1;int left = 0, right = 0;for (int i = 3; i <= n; ++i) {for (int j = 1; j <= i / 2; ++j) {left = max(j, dp[j]);right = max(i - j, dp[i - j]);dp[i] = max(left * right, dp[i]);}}return dp[n];}
- 这里left取最值那一步是可以省略的,为什么?
- 因为代码实现方法是对j和i- j同时判断是否需要拆分,但是就算 j 它再怎么拆也是拆分成1 - i之间的某个元素再加上另外一个数或一组数(省去left取最值写法其实把这一个数或一组数包到dp[i - j]里了),所以,取到最值的时候,j 一定是1- i之间的某个值,然后dp序列是递增的,那么最值一定不在后 i / 2 里(随着基数增大),所以 j 的上界可以是 i / 2。
- 数学证明如下(节选自力扣题解的某位同学回答):
- 因为j * dp[i - j]包含了dp[j] * dp[i - j],这是可以证明的: 对j最优拆分:j = a1 + a2 +…+an; 对i - j 最优拆分:i - j = b1 + b2 +…+bn; 所以有 dp[j] = a1 * a2 … an; dp[i - j] = b1 * b2 *… bn; dp[i] * dp[i - j] = (a1 *a2 *…an) * (b1 * b2 … bn) = a1 * (a2 * … * an * b1 * b2 … bn) 令 k = a1,必有i - k = a2 + … + an + b1 + b2 +…+ bn(这就是对 i - k 的一种拆分) 也就是说如果以上这种对i - k的一种拆分是最优的,那么必有dp[j] * dp[i - j] = k * dp[i - k] 所以此时j * dp[i - j]包含dp[j] * dp[i - j]; 如果以上这种对i - k的拆分不是最优的,那这种拆分方案虽不会被j * dp[i - j]包含但也不会是答案;
96.不同的二叉搜索树
力扣题目链接
题目描述:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
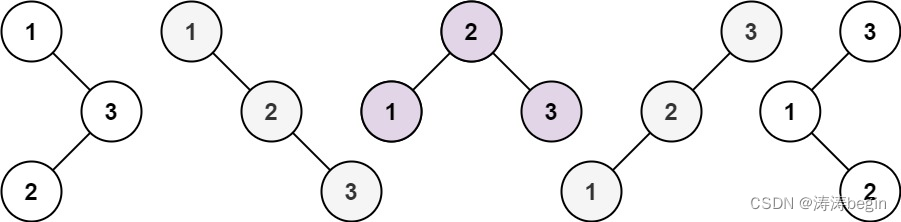
输入:n = 3
输出:5
思路:
- 我的思路是这样的,1到n的每个数字都可以作为根节点,那么外层for循环还是老套度去求dp数组,内层for循环去决定哪个数子作为根节点,然后将左右节点的dp值乘起来,然后不断加到dp[i]上。
- 动态规划五部曲:
- 分析dp数组含义:dp[ i ]数组代表下标为i的整数的二叉树种类
- 分析递推公式:
dp[n] = dp[n - 1] * dp[0] + dp[n - 2] * dp[1] + ... + dp[1]*dp[n - 2] + dp[0]* dp[n - 1] - dp数组初始化:因为我们左子树可以是0个节点,而且我们要做乘法,所以下标0赋值为1,把下标1也赋值为1,遍历的时候下标从2开始
- 遍历顺序:显然是从前往后遍历,我们遍历的时候从下标 i = 2开始,那么外层for循环还是老套度去求dp数组,内层for循环去决定哪个数子作为根节点,然后将左右子树节点数的dp值乘起来,然后不断加到dp[i]上。
- 推导数组结果:1 1 2 5 14…
代码实现
int numTrees(int n) {if (n < 2) return 1;//dp[n] = dp[n - 1] * dp[0] + dp[n - 2] * dp[1] + ... + dp[1]*dp[n - 2] + dp[0]* dp[n - 1]vector<int> dp(n + 1);dp[0] = 1, dp[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 1; j <= i; ++j) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}