课上

前序，根左右

中序，左根右

若前序中序相同，则树都没有左节点

求树的高度

表达式树

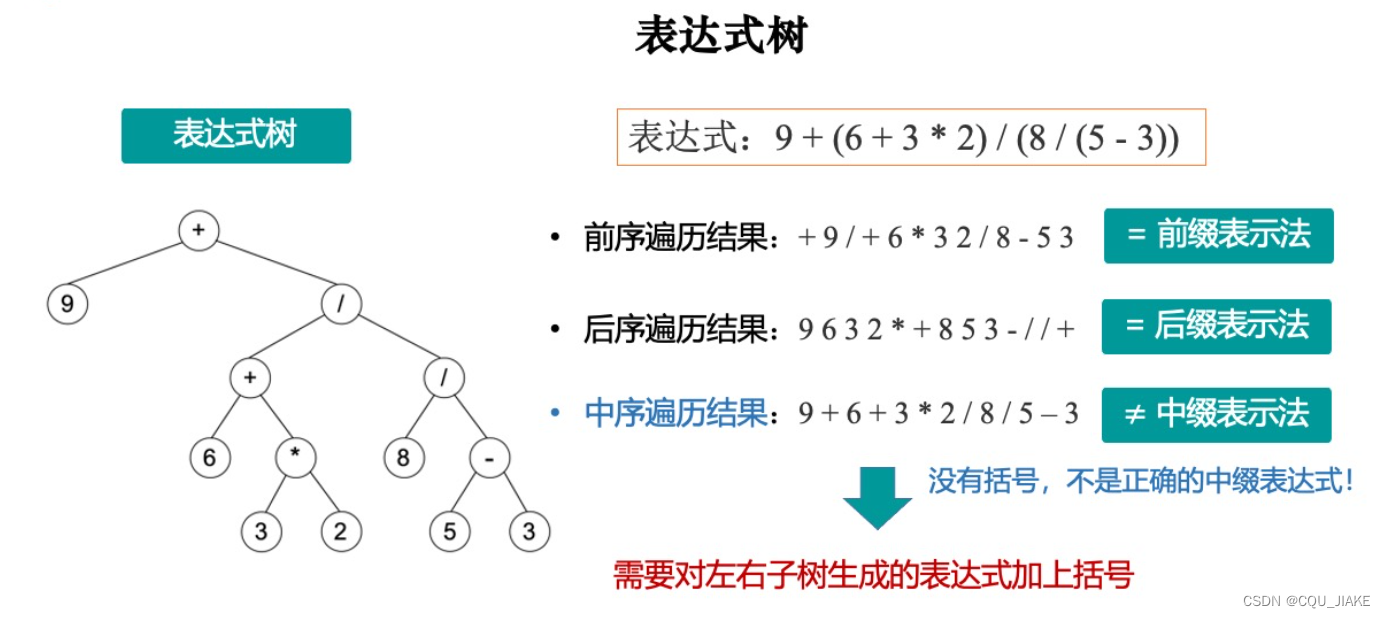
中缀表达式树

主要考虑括号问题

这个就是考虑递归底层，要结束时的情形；以及根节点的情形；

由于表达式树是满树，不会出现度为1的结点，所以要么是叶子结点，即递归的终点；

要么是有两个孩子的父节点，递归输出左右子树

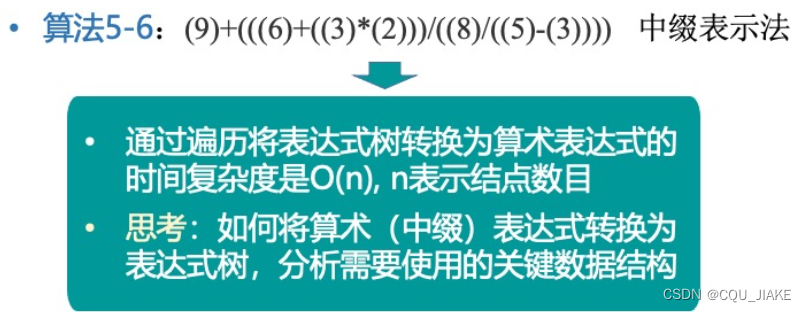
非递归实现前序遍历

非递归，就是用栈结构模拟，先进后出

每次循环都干了两件事，第一件事是先沿左分支一直往下走，直到走不下去，并且把沿途的结点都记录到栈中；第二件事就是左不下去了，然后重新赋值为最后一个左节点，并且把其从栈里取出来，然后尝试得到它的右节点，得到右结点后，不在本层迭代中用，而是在下次迭代中用。

第一件事的终止条件说的是该结点为空，即遍历到的为叶子结点，它结束的时候，指针结点一定是空结点，即一定访问到了最底层，所以第二件事的if里，第一步就是重新把栈的顶部元素赋值给结点，但是一定不要让栈里元素再次回到循环里，否则就会形成死循环，所以无论有没有右孩子，都要把那个栈顶结点的右孩子赋值给树结点，如果有右孩子，那么就是接着先序遍历其右孩子，如果没有，在下次循环里就不会继续进行，而是得到下一个栈顶元素，即开始往回遍历找右孩子了

后续的非递归

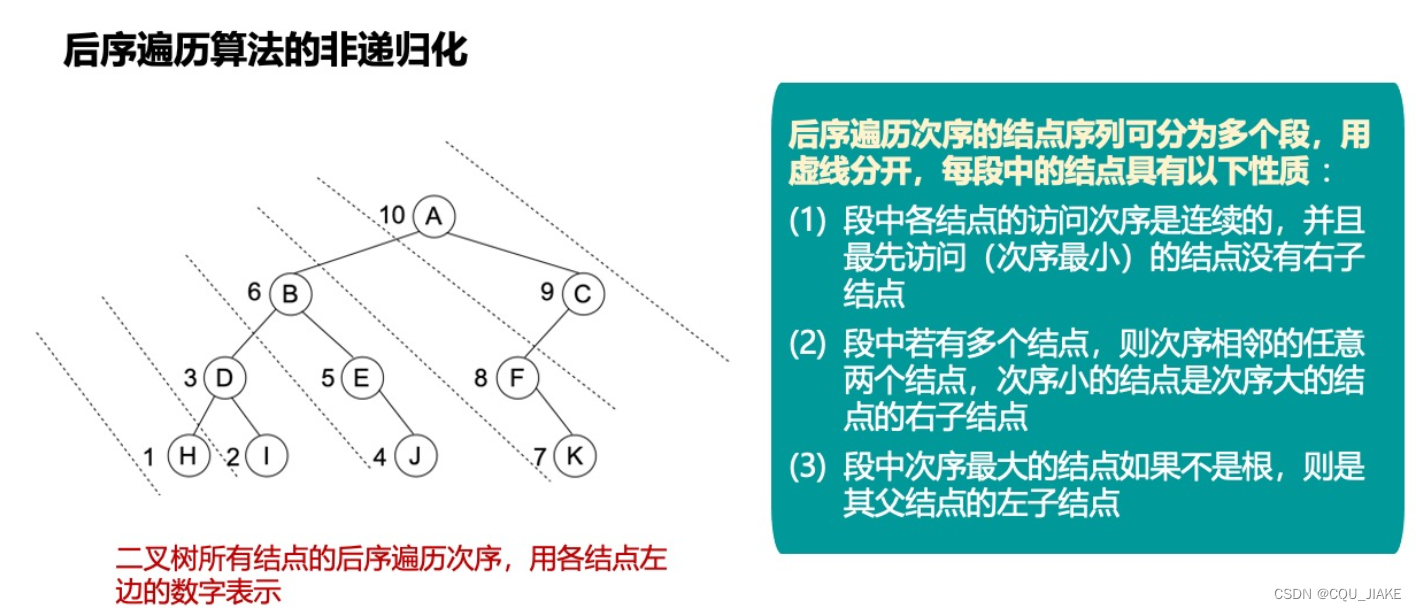
第二种思想就是根据非递归的前序得到非递归的后序

前序：根左右  后续：左右根

后序的反转为，根右转左转。

右转就是说它右子树里面也都反转了，就是递归进行反转，向下多层都进行了反转，而不是只在最外层进行了一次反转。

所以用非递归前序就是非递归进行前序遍历时，先遍历右子树，再遍历左子树，就是位置交换了一下，这样就得到了后序的反转序列，再反转一次，就得到了通过非递归前序实现的非递归后序序列

层序遍历树

检验奇偶树

1.层序

就是建立两个队列，两个队列中的元素一一对应，其实可以用一个结构体（即树结点与其深度组成）队列

2.深度

用且的关系，即左右必须都得是奇偶树才行

额外要求

1.层序

2.dfs

层序遍历对每一层的结点是从左到右，深度优先也是从左到右，不过不一定连续，层序遍历一定连续。

由于不连续，所以就用一个数组来记录上一个访问到的该层数的结点的值，类似于数组计数思想