回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测

效果一览

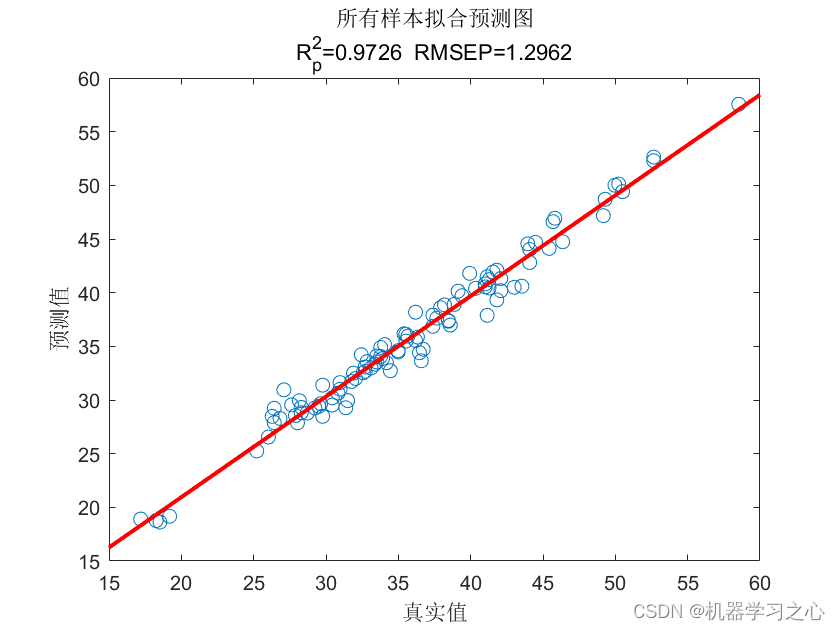
基本介绍

1.RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测 可直接运行Matlab;
2.评价指标包括: R2、MAE、RMSE和MAPE等，代码质量极高，方便学习和替换数据。要求2021版本及以上。
3.2023年新算法霜冰优化算法RIME优化的参数为:CNN的批处理大小、学习率、正则化系数，能够避免人工选取参数的盲目性，有效提高其预测精度。
4.main.m为主程序，其他为函数文件，无需运行，data为数据，多输入单输出，数据回归预测，输入7个特征，输出1个变量，直接替换Excel数据即可用!注释清晰，适合新手小白~

程序设计

• 完整程序和数据获取方式：私信博主回复Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测；

while it <= Max_iteritRimeFactor = (rand-0.5)*2*cos((pi*it/(Max_iter/10)))*(1-round(it*W/Max_iter)/W);%Parameters of Eq.(3),(4),(5)E =(it/Max_iter)^0.5;%Eq.(6)newRimepop = Rimepop;%Recording new populationsnormalized_rime_rates=normr(Rime_rates);%Parameters of Eq.(7)for i=1:Nfor j=1:dim%Soft-rime search strategyr1=rand();if r1< EnewRimepop(i,j)=Best_rime(1,j)+RimeFactor*((Ub(j)-Lb(j))*rand+Lb(j));%Eq.(3)end%Hard-rime puncture mechanismr2=rand();if r2<normalized_rime_rates(i)newRimepop(i,j)=Best_rime(1,j);%Eq.(7)endendendfor i=1:N%Boundary absorptionFlag4ub=newRimepop(i,:)>ub;Flag4lb=newRimepop(i,:)<lb;newRimepop(i,:)=(newRimepop(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;newRime_rates(1,i)=fobj(newRimepop(i,:));%Positive greedy selection mechanismif newRime_rates(1,i)<Rime_rates(1,i)Rime_rates(1,i) = newRime_rates(1,i);Rimepop(i,:) = newRimepop(i,:);if newRime_rates(1,i)< Best_rime_rateBest_rime_rate=Rime_rates(1,i);Best_rime=Rimepop(i,:);endendend

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229