【机器学习】四、计算学习理论

1 基础知识

计算学习理论（computational learning theory）：关于通过“计算”来进行“学习”的理论，即关于机器学习的理论基础，其目的是分析学习任务的困难本质，为学习算法体统理论保证，并根据结果指导算法设计。

对于二分类问题，给定样本集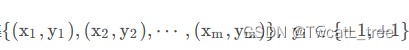在这里插入图片描述
假设所有样本服从一个隐含未知的分布D DD，所有样本均独立同分布（independent and identically distributed）。

令h为样本到{ − 1 , + 1 } 上的一个映射，其泛化误差为
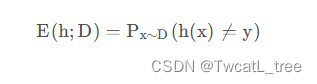
$E ( h ; D ) = P x ∼ D ( h ( x ) ≠ y ) E(h;D)=P_{x\sim D}(h(x)\neq y) E(h;D)=P x∼D (h(x)  =y)$

h在D 的经验误差为
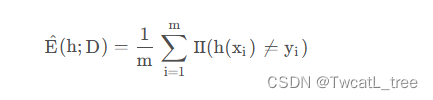
在这里插入图片描述

由于D是D的独立同分布采样，因此h hh的经验误差的期望等于其泛化误差。在上下文明确时，我们将E ( h ; D ) 和E ^ ( h ; D ) 分别简记为E ( h )和E ^ ( h ) 。令ϵ为E ( h ) 的上限，即E ( h ) ≤ ϵ E(h)；我们通常用ϵ表示预先设定的学得模型所应满足的误差要求，亦称“误差参数”。

我们将研究经验误差和泛化误差之间的逼近程度；若h在数据集上的经验误差为0，则称h与D一致，否则称其不一致。对于任意两个映射h 1 , h 2 ∈ X → Y h_1,h_2，用不合（disagreement）来度量他们之间的差别：
d ( h 1 , h 2 ) = P x ∼ D ( h 1 ( x ) ≠ h 2 ( x ) )
我们将会用到几个常见的不等式：

Jensen不等式：对任意凸函数，有
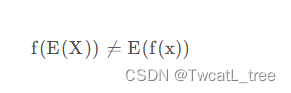
$f ( E ( X ) ) ≠ E ( f ( x ) ) f(E(X))\neq E(f(x)) f(E(X))  =E(f(x))$

Hoeffding不等式：若x 1 , x 2 , … , x m
为m 个独立随机变量，且满足0 ≤ x i ≤ 1，对任意ϵ > 0，有
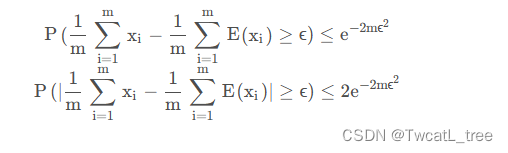
在这里插入图片描述

McDiarmid不等式：
在这里插入图片描述

2 PAC学习

概率近似正确理论（Probably Approximately Correct，PAC）：

首先介绍两个概念：

C：概念类。表示从样本空间到标记空间的映射，对任意样例，都能使得c ( x ) = y 。
H ：假设类。学习算法会把认为可能的目标概念集中起来构成H。
若c ∈ H ，则说明假设能将所有示例按真实标记一致的方式完全分开，称为该问题对学习算法而言是”可分的“；否则，称为”不可分的“
对于训练集，我们希望学习算法学习到的模型所对应的假设h hh尽可能接近目标概念c。我们是希望以比较大的把握学得比较好的模型，也就是说，以较大的概率学得误差满足预设上限的模型，这就是"概率近似正确"的含义。形式化地说，令δ 表示置信度，可定义:

PAC辨识：对0 ≤ ϵ , δ < 1 ，所有的c ∈ C 和分布D ，若存在学习算法，其输出假设h ∈ H 满足：
$P ( E ( h ) ≤ ϵ ) ≥ 1 − δ P(E(h)\le \epsilon)\ge 1- \delta P(E(h)≤ϵ)≥1−δ$

在这里插入图片描述

$PAC学习中一个关键因素是假设空间H的复杂度。H包含了学习算法所有可能输出的假设，若在PAC学习中假设空间与概念类完全相同，即H=C，这称为"恰PAC可学习" (properly PAC learnable)。直观地看，这意味着学习算法的能力与学习任务”恰好匹配“。然而，这种让所有候选假设都来自概念类的要求看似合理，但却并不实际，因为在现实应用中我们对概念类C CC通常一无所知，更别说获得一个假设空间与概念类恰好相同的学习算法。显然，更重要的是研究假设空间与概念类不同的情形，即H ≠ C H\neq CH  =C。一般而言，H HH越大，其包含任意目标概念的可能性越大，但从中找到某个具体目标概念的难度也越大。∣ H ∣ |H|∣H∣有限时，我们称究为"有限假设空间"，否则称为"无限假设空间"。$