时间复杂度的计算技巧-算法模型中的时间复杂度如何计算，有哪些技巧呢

大家好，我是微学AI，今天给大家介绍一下时间复杂度的计算技巧-算法模型中的时间复杂度如何计算，有哪些技巧呢，算法的时间复杂度是评估算法性能和效率的一种方式，它表示算法需要执行多少次基本操作才能完成其任务，这个数量随着输入规模的增加而增加。
时间复杂度通常用大O符号表示，例如O(n)、O(n²)等。其中，n表示输入规模，也就是算法需要处理的数据的大小。
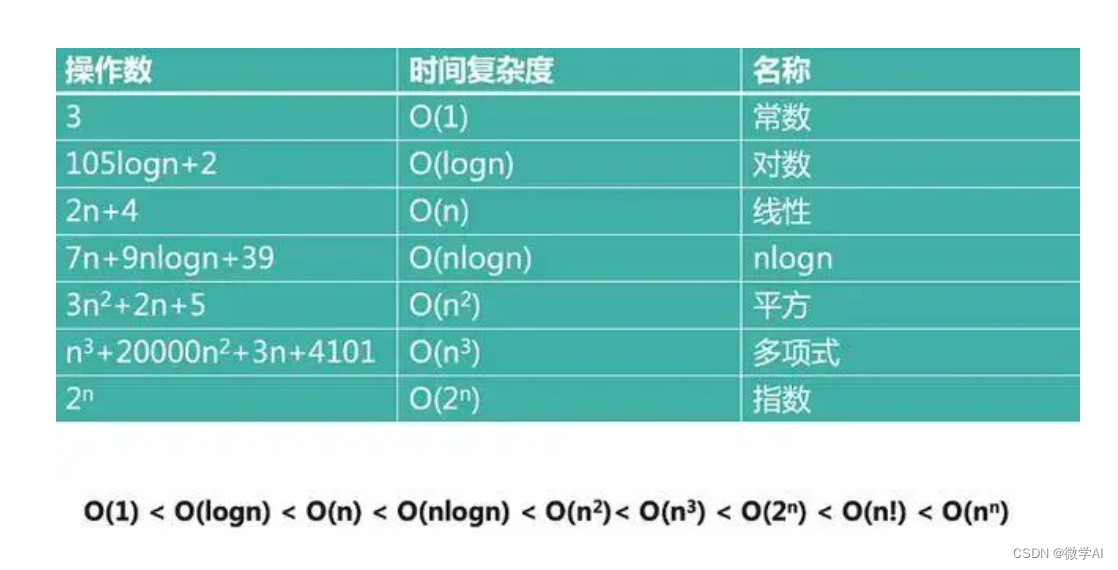
在这里插入图片描述

一、常见的时间复杂度有：

O(1)：常数时间复杂度，表示算法的执行时间不随输入规模的增加而增加，例如数组的索引访问。
O(log n)：对数时间复杂度，表示算法的执行时间随着输入规模的增加而增加，但增加速度很慢，例如二分查找。
O(n)：线性时间复杂度，表示算法的执行时间随着输入规模的增加而线性增加，例如遍历数组。
O(n log n)：线性对数时间复杂度，表示算法的执行时间随着输入规模的增加而略微超线性增加，例如快速排序。
O(n²)：平方时间复杂度，表示算法的执行时间随着输入规模的增加而平方级别增加，例如冒泡排序。

对于同一问题，不同的算法可能具有不同的时间复杂度，因此在选择算法时需要综合考虑时间复杂度、空间复杂度以及算法的实现难度等因素。

二、在C语言中的算法时间复杂度

我们可以通过对程序执行的次数的统计来计算其时间复杂度。一般情况下，我们关注的是最坏情况下程序的执行次数，因为最坏情况下的时间复杂度往往是算法的瓶颈。

对于一个基本操作（如赋值、比较、运算等），我们假设其执行时间为常量单位时间（即 O(1) 时间复杂度）。那么我们可以根据程序的代码结构和控制流程，计算出程序在最坏情况下的执行次数，从而确定其时间复杂度。下面是一些常见的时间复杂度及其示例：

O(1) 常数级别

int a = 1;
int b = 2;
int c = a + b;

上述代码中，三个赋值语句和一个加法运算都是 O(1) 操作，总的时间复杂度也是 O(1)。

O(n) 线性级别

for (int i = 0; i < n; i++) {printf("%d ", i);
}

上述代码中，for 循环中的 printf 语句会被执行 n 次，因此总的时间复杂度是 O(n)。

O(n^2) 平方级别

for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {printf("%d ", i + j);}
}

上述代码中，内层循环中的 printf 语句会被执行 n^2 次，因此总的时间复杂度是 O(n^2)。

O(log n) 对数级别

int i = n;
while (i > 0) {printf("%d ", i);i /= 2;
}

上述代码中，while 循环的条件是 i > 0，每次循环 i 会被除以 2，因此循环执行的次数为 log2(n)+1（以 2 为底的对数），因此总的时间复杂度是 O(log n)。

O(n log n) 线性对数级别

for (int i = 0; i < n; i++) {int j = n;while (j > 0) {printf("%d ", i + j);j /= 2;}
}

上面代码中，外层循环会被执行 n 次，内层循环会被执行 log2(n)+1 次，因此总的时间复杂度是 O(n log n)。

计算时间复杂度时，一般采用大 O 记法，去掉常数项和低次项，只保留最高次项。另外，在计算时间复杂度时，需要注意以下几点：

循环嵌套时，内层循环次数的上界应该是外层循环的变量。
递归算法的时间复杂度需要进行递推处理，通常会使用主定理或递归树等方法。
位运算、矩阵乘法等特殊运算的时间复杂度需要特别处理。

三、递归算法的时间复杂度(python)

当涉及递归算法的时间复杂度时，有几种常见的复杂度级别。下面我将为你提供每种级别的例子代码：

O(1) 常数级别的递归算法

def recursive_constant(n):if n <= 0:returnprint("Hello!")recursive_constant(n - 1)

上述代码中，无论输入是多少，函数都只会递归调用自身一次，因此时间复杂度为 O(1)。

O(n) 线性级别的递归算法

def recursive_linear(n):if n <= 0:returnprint(n)recursive_linear(n - 1)

上述代码中，递归调用的次数与输入规模 n 成线性关系，因此时间复杂度为 O(n)。

O(n^2) 平方级别的递归算法

def recursive_quadratic(n):if n <= 0:returnfor i in range(n):print(n)recursive_quadratic(n - 1)

上述代码中，递归调用的次数与输入规模 n 成平方关系，这个函数的时间复杂度是O(n^2)，其中n表示输入的参数值。

我们来分析一下：

该函数是一个递归函数，每次递归调用都会执行一个for循环，循环次数为n。然后，递归调用将参数n减1，并再次执行相同的操作。

因此，在第一次递归调用中，for循环会执行n次。在第二次递归调用中，for循环会执行n-1次，以此类推，直到n减少到1为止。

总的执行次数可以近似为n + (n-1) + (n-2) + … + 1。根据等差数列求和公式，可以得到：

n + (n-1) + (n-2) + … + 1 = (n+1) * n / 2

因此，总的执行次数约为(n+1) * n / 2，也就是O(n^2)。

O(2^n) 指数级别的递归算法

def recursive_exponential(n):if n <= 0:returnprint(n)recursive_exponential(n - 1)recursive_exponential(n - 1)

这个函数的时间复杂度是O(2^n)，其中n表示输入的参数值。让我们来分析一下：

该函数是一个递归函数，每次递归调用都会执行两个递归调用。在每个递归调用中，参数n都会减1，并再次执行相同的操作。

因此，在第一次递归调用中，函数会执行一次print语句和两次递归调用。在第二次递归调用中，每次递归调用又会执行一次print语句和两次递归调用。以此类推，直到n减少到0为止。

总的执行次数可以近似为2^0 + 2^1 + 2^2 + … + 2^n。根据等比数列求和公式，可以得到：

2^0 + 2^1 + 2^2 + … + 2^n = 2^(n+1) - 1

因此，总的执行次数约为2^(n+1) - 1，也就是O(2^n)。

需要注意的是，递归函数的空间复杂度是O(n)，因为每次递归调用都会在内存中创建新的函数调用栈。

四、 O(nlogn)与O(n^2logn)的时间复杂度：

1.O(nlogn)的例子

def merge_sort(arr):if len(arr) <= 1:return arr# 分割数组mid = len(arr) // 2left = merge_sort(arr[:mid])right = merge_sort(arr[mid:])# 合并并排序子数组return merge(left, right)def merge(left, right):merged = []i, j = 0, 0# 依次比较两个子数组的元素，并按顺序合并while i < len(left) and j < len(right):if left[i] < right[j]:merged.append(left[i])i += 1else:merged.append(right[j])j += 1# 将剩余的元素添加到合并后的数组中merged.extend(left[i:])merged.extend(right[j:])return mergedarr = [4, 2, 7, 1, 5, 3]
sorted_arr = merge_sort(arr)
print(sorted_arr)

以上示例使用归并排序算法对一个数组进行排序，归并排序的时间复杂度为O(nlogn)。在每次递归中，数组会被分割成两半，每一层递归需要O(n)的时间复杂度来合并两个已排序的子数组。

O(n^2logn)的例子：

def insertion_sort(arr):for i in range(1, len(arr)):key = arr[i]j = i - 1# 在已排序的子数组中找到合适的位置插入元素while j >= 0 and arr[j] > key:arr[j+1] = arr[j]j -= 1arr[j+1] = keydef nested_insertion_sort(arr):for i in range(len(arr)):insertion_sort(arr)return arrarr = [4, 2, 7, 1, 5, 3]
sorted_arr = nested_insertion_sort(arr)
print(sorted_arr)