拓扑排序--C++实现

1. 定义

前置知识

DAG: Directed Acyclic Graph 有向无环图
拓扑序：像先修课程一样，即任意课程的前置课程都在其前面。

举个例子

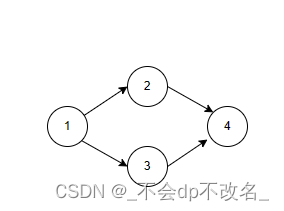
在这个图中，1234或者1324是拓扑序。而其他的序列不是，即在一个节点出现之前他的所有祖先节点需要出现。

2. 实现

2.1 DFS

任意选节点，先递归各个子节点，在将根节点放入栈中。最后将栈中元素弹出，即可得到一个拓扑序列。相当于二叉树的后序遍历。

由于存在可能有环的情况，所有节点的状态需要三个状态位来表示以防止和遍历过的冲突。


struct Graph {Graph(int vertex_num = 100):maxVertexSz(vertex_num + 1),graph(vertex_num + 1,std::vector<int>( vertex_num + 1, 0)){}enum Status{to_visit,visiting,visited};void add_edge(int u, int v){graph[u][v] = 1;}bool find_edge(int u, int v) const{return graph[u][v];}std::unordered_set<int> getVertexSet() const{std::unordered_set<int> vertexSet;for (int i = 0; i < maxVertexSz; ++i)for (int j = 0; j < maxVertexSz; ++j)if (graph[i][j])vertexSet.insert(i), vertexSet.insert(j);return vertexSet;}void cal_inDeg(std::vector<int> &inDeg){for (int i = 0; i < maxVertexSz; ++i)for (int j = 0; j < maxVertexSz; ++j)if (graph[i][j])inDeg[j]++;}std::vector<std::vector<int>> graph;int maxVertexSz;
};bool topo_sort_dfs(const Graph &p, std::vector<Graph::Status> &stat,std::stack<int> &st,int node) {if (stat[node] == Graph::visited)return true;if (stat[node] == Graph::visiting)return false;stat[node] = Graph::visiting;bool not_cyclic = true;for (int i = 0; i < p.maxVertexSz; ++i) {if (!not_cyclic)return false;if (p.graph[node][i] != 0) {not_cyclic = topo_sort_dfs(p, stat, st, i);}}st.push(node);stat[node] = Graph::visited;
}std::vector<int> topo_dfs(const Graph &p)
{std::vector<int> topo_seq;std::unordered_set<int> vertexSet(std::move(p.getVertexSet()));std::vector<Graph::Status> stat(p.maxVertexSz, Graph::to_visit);std::stack<int> st;bool not_cyclic = true;for (auto node:vertexSet) {if (not_cyclic && stat[node] == Graph::to_visit)not_cyclic = topo_sort_dfs(p, stat, st, node);}if ( not_cyclic ) {while (!st.empty()) {topo_seq.push_back(st.top());st.pop();}}return topo_seq;
}

2.2 Kahn’s

先计算出所有节点的入度，再将入度为0的节点放入队列中。每次从队列中取出一个节点放入拓扑序列，并根据以该节点为入点的边，降低从该节点到达节点的入度。若降低后节点入度为0，则放入队列中。

其实相当于BFS。
注意对比拓扑序列的序列长度，若长度比节点数目少，则说明图中有环。

std::vector<int> topo_sort_kahn(const Graph &p)
{std::vector<int> topo_seq;int sz = p.maxVertexSz;std::vector<int> inDeg(sz, 0);std::unordered_set<int> vertexSet(std::move(p.getVertexSet()));std::queue<int> q;for ( int i = 0; i < sz; ++i) {for ( int j = 0; j < sz; ++j) {if (p.graph[i][j])inDeg[j]++;}}for (int node:vertexSet) {if (vertexSet.count(node) && !inDeg[node])q.push(node);}while (!q.empty()) {int cur = q.front();topo_seq.push_back(cur);q.pop();for (int i = 0; i < sz; ++i ) {if ( p.graph[cur][i] ) {inDeg[i]--;if (!inDeg[i])q.push(i);}}}return topo_seq;
}