题目
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi 用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0 < N , V ≤ 1000
0 < vi , wi ≤ 1000
思路
两层循环:
外层:循环遍历每一个物品
内层:在当前物品放入背包中,求出在背包有不同容量时装入物品的最大值。
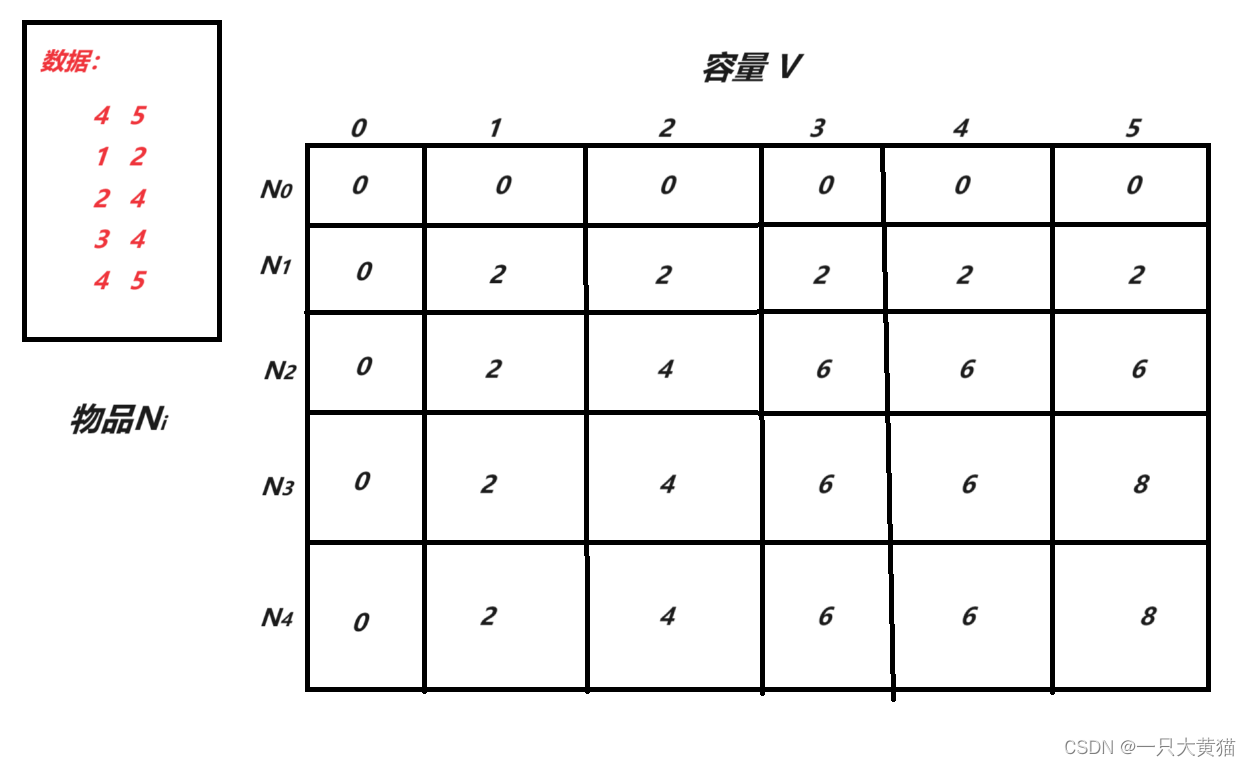
手动模拟:
注意:在背包容量为0,或者没有物品的时候,背包内物品的最大价值为0;
遍历第1个物品:
背包容积为1的时候:可以将该物品1放入,总价值为2。
背包容积为2的时候:可以将该物品1放入,总价值为2。
背包容积为3的时候:可以将该物品1放入,总价值为2。
背包容积为4的时候:可以将该物品1放入,总价值为2。
背包容积为5的时候:可以将该物品1放入,总价值为2。
遍历第2个物品:
背包容积为1的时候:可以将该物品1放入,总价值为2。
背包容积为2的时候:可以将该物品2放入,总价值为4。
背包容积为3的时候:可以将该物品1、2放入,总价值为6。
背包容积为4的时候:可以将该物品1、2放入,总价值为6。
背包容积为5的时候:可以将该物品1、2放入,总价值为6。
遍历第3个物品:
背包容积为1的时候:可以将该物品1放入,总价值为2。
背包容积为2的时候:可以将该物品2放入,总价值为4。
背包容积为3的时候:可以将该物品1、2放入,总价值为6。
背包容积为4的时候:可以将该物品1、2放入,总价值为6。
背包容积为5的时候:可以将该物品1、2、3放入,总价值为8。
遍历第4个物品:
背包容积为1的时候:可以将该物品1放入,总价值为2。
背包容积为2的时候:可以将该物品2放入,总价值为4。
背包容积为3的时候:可以将该物品1、2放入,总价值为6。
背包容积为4的时候:可以将该物品1、2放入,总价值为6。
背包容积为5的时候:可以将该物品1、2、3放入,总价值为8。
可以得出:
状态转移方程: f[ i ][ j ] = max(f[ i ][ j ],f[ i - 1 ][ j - v[ i ] ] + w[ i ]);
代码1
//二维数组版
#include<bits/stdc++.h>
using namespace std;const int N = 1010;
int n,m;// n代表物品个数,m代表背包容量
int v[N],w[N];
int f[N][N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++)// 物品循环{for(int j = 0; j <= m; j ++)// 容量循环{f[i][j] = f[i - 1][j];if(j >= v[i]) f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);}}cout << f[n][m] << endl;return 0;
}
优化
通过手动模拟,我们可以发现,不需要二维数组就可以存储数据,为了数据防止被覆盖,内层循环需要从m依次循环到v[ i ];
状态转移方程:
f[ j ] = max( f[ j ],f[ j - v[ i ] ] + w[ i ]);
代码2
// 优化为一维数组版
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n,m;// n代表物品个数,m代表背包容量
int v[N],w[N],f[N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++)// 物品循环for(int j = m; j >= v[i]; j --)// 容量循环f[j] = max(f[j],f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;
}