1.如何实现统一的API前缀-web组件篇

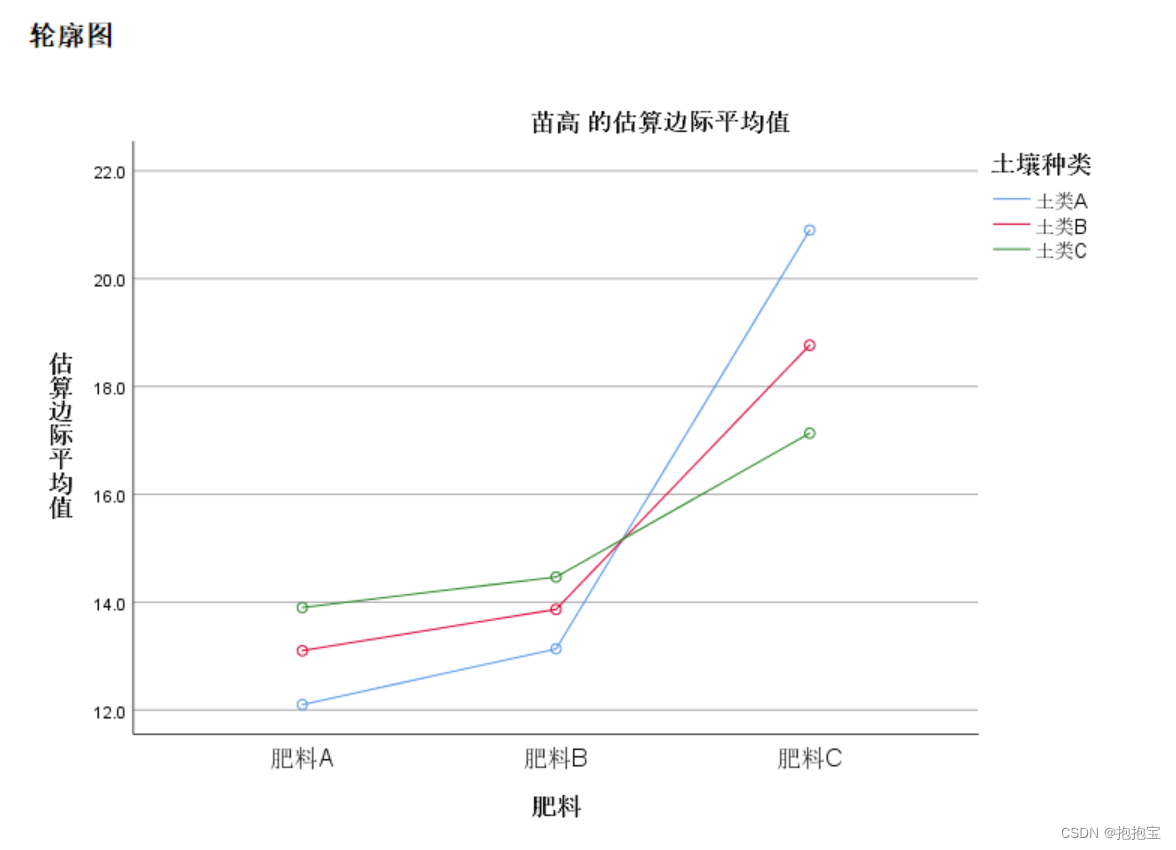
文章目录

  • 1. 问题的由来
  • 2.实现原理
  • 3. 总结

1. 问题的由来

系统提供了 2 种类型的用户，分别满足对应的管理后台、用户 App 场景。
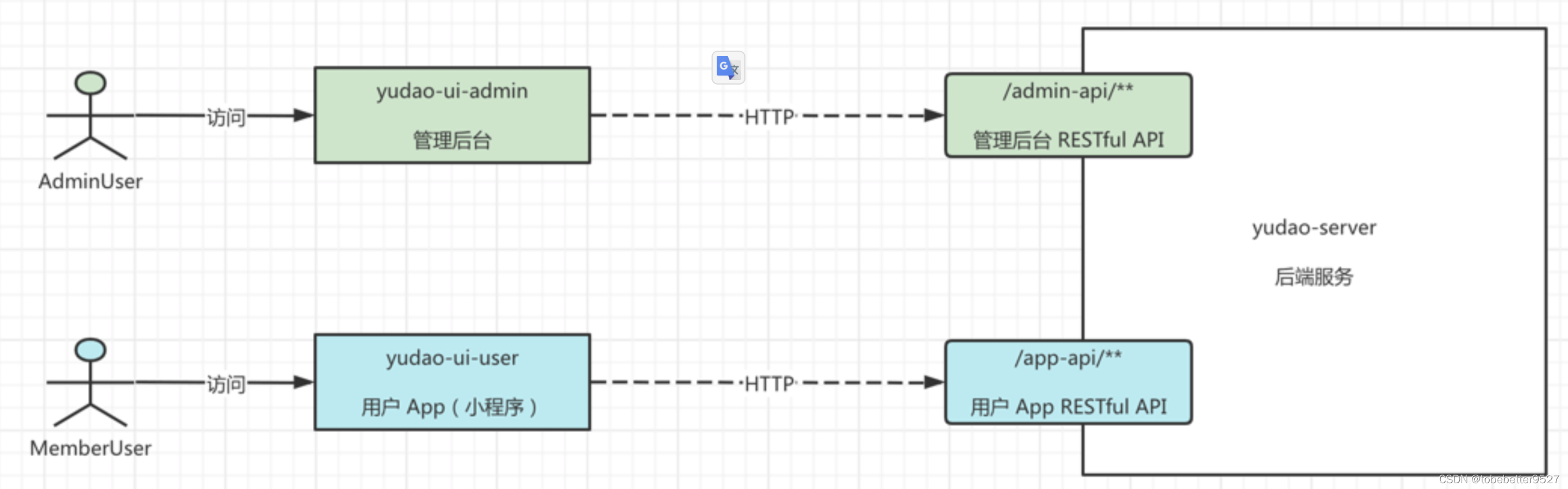
在这里插入图片描述
两种场景的前缀不同，分别为/admin-api/和/app-api/，都写在一个controller里面，显然比较混乱。分开写在不同的controller是比较好的方案。

2.实现原理

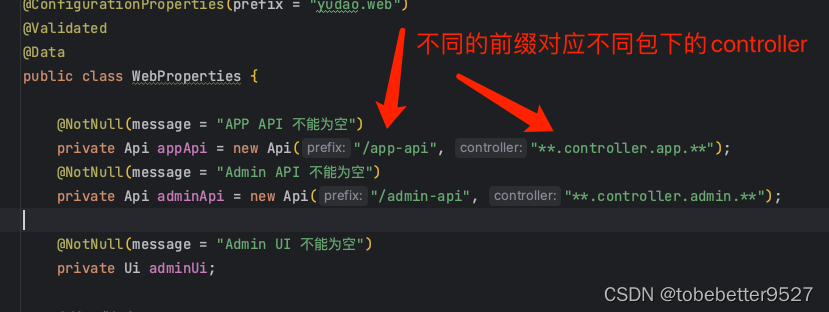
查看组件yudao-spring-boot-starter-web的类YudaoWebAutoConfiguration。
在这里插入图片描述
再来看WebProperties类

在这里插入图片描述

3. 总结

实现spring-mvc的接口WebMvcConfigurer，定制请求路径的前缀匹配方式。利用AntPathMatcher匹配路径。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/180868.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Mgeo：multi-modalgeographic language model pre-training

Mgeo：multi-modalgeographic language model pre-training

文章目录 question5.1 Geographic Encoder5.1.1 Encoding5.1.2 5.2 multi-modal pre-training 7 conclusionGeo-Encoder: A Chunk-Argument Bi-Encoder Framework for Chinese Geographic Re-Rankingabs ERNIE-GeoL: A Geography-and-Language Pre-trained Model and its Appli…
阅读更多...
Gradle笔记 一 Gradle的安装与入门

Gradle笔记 一 Gradle的安装与入门

文章目录 Gradle 入门Gradle 简介学习Gradle 的原因： 常见的项目构建工具Gradle 安装Gradle 安装说明安装JDK 下载并解压到指定目录配置环境变量检测是否安装成功 Gradle 项目目录结构Gradle 创建第一个项目Gradle 中的常用指令修改maven 下载源Wrapper 包装器使用教…
阅读更多...
【C++】继承

【C++】继承

本期我们来学习c中的继承 目录 一、啥是继承 二、继承的定义 1.1 定义格式 1.2 继承方式 三、基类和派生类对象赋值转换 四、继承中的作用域 五、派生类的默认成员函数 5.1 派生类的构造函数和基类构造函数的关系 5.2 派生类的拷贝函数和基类拷贝函数的关系 5.3 派生…
阅读更多...
Python算法例7 四数乘积

Python算法例7 四数乘积

1. 问题描述 给定一个长度为n的数组a和一个正整数k，从数组中选择四个数，要求四个数的乘积小于等于k，求方案总数。 2. 问题示例 给定n5，a[1，1，1，2，2]，k3，返…
阅读更多...
小程序day02

小程序day02

目标 WXML模板语法 数据绑定 事件绑定 那麽問題來了，一次點擊會觸發兩個組件事件的話，該怎么阻止事件冒泡呢？ 文本框和data的双向绑定 注意点: 只在标签里面用value“{{info}}”，只会是info到文本框的单向绑定，必须在…
阅读更多...
【Linux】多路IO复用技术②——poll详解如何使用poll模型实现简易的一对多服务器（附图解与代码实现）

【Linux】多路IO复用技术②——poll详解如何使用poll模型实现简易的一对多服务器（附图解与代码实现）

在阅读本篇博客之前，建议大家先去看一下我之前写的这篇博客，否则你很可能会一头雾水 【Linux】多路IO复用技术①——select详解&如何使用select模型在本地主机实现简易的一对多服务器（附图解与代码实现）http://t.csdnimg.cn/…
阅读更多...
JavaEE平台技术——预备知识（Web、Sevlet、Tomcat）

JavaEE平台技术——预备知识（Web、Sevlet、Tomcat）

JavaEE平台技术——预备知识（Web、Sevlet、Tomcat） 1. Web基础知识2. Servlet3. Tomcat并发原理 1. Web基础知识 🆒🆒上个CSDN我们讲的是JavaEE的这个渊源，实际上讲了两个小时的历史课，给大家梳理了一下&a…
阅读更多...
为机器学习算法准备数据（Machine Learning 研习之八）

为机器学习算法准备数据（Machine Learning 研习之八）

本文还是同样建立在前两篇的基础之上的！ 属性组合实验 希望前面的部分能让您了解探索数据并获得洞察力的几种方法。您发现了一些数据怪癖，您可能希望在将数据提供给机器学习算法之前对其进行清理，并且发现了属性之间有趣的相关性&#xff0c…
阅读更多...
Web自动化测试 —— PageObject设计模式！

Web自动化测试 —— PageObject设计模式！

一、page object 模式简介 1.1、传统 UI 自动化的问题 无法适应 UI 频繁变化无法清晰表达业务用例场景大量的样板代码 driver/find/click 二、page object 设计原则 2.1、POM 模式的优势 降低 UI 变化导致的测试用例脆弱性问题让用例清晰明朗，与具体实现无关 2.…
阅读更多...
三、操作系统

三、操作系统

（一）概述 操作系统是管理整个系统的软、硬件资源的系统，既是人和硬件之间的一种接口，也是应用软件与硬件之间的接口。 （二）进程管理 1.进程的状态 进程的状态是操作系统对进程进行管理的时候设置的几种状…
阅读更多...
Gopro hero5运动相机格式化后恢复案例

Gopro hero5运动相机格式化后恢复案例

Gopro运动相机以稳定著称，旗下的Hero系列销售全球。下面我们来看一个Hero5格式化后拍了少量素材的恢复案例。 故障存储:64G MicroSD卡 Exfat文件系统 故障现象: 64G的卡没备份数据时做了格式化操作又拍了一条，发现数据没有备份，客户自行使…
阅读更多...
c语言经典算法—二分查找，冒泡，选择，插入，归并，快排，堆排

c语言经典算法—二分查找，冒泡，选择，插入，归并，快排，堆排

一、二分查找 1、前提条件&#xff1a;数据有序&#xff0c;随机访问&#xff1b; 2、实现&#xff1a;递归实现&#xff0c;非递归实现 3、注意事项&#xff1a; 循环退出条件:low <high,low high.说明还有一个元素&#xff0c;该元素还要与key进行比较 mid的取值&#xf…
阅读更多...
C# list＜T＞去重

C# list＜T＞去重

文章目录 C# list<T>去重值类型去重List<object>object is intobject is decimalobject is charobject is boolobject is string List<int>List<string> 引用类型去重 C# list去重 值类型去重 List object is int //object is intList<object&g…
阅读更多...
Redis-命令操作Redis

Redis-命令操作Redis

&#x1f3ac; 艳艳耶✌️&#xff1a;个人主页 &#x1f525; 个人专栏 &#xff1a;《Spring与Mybatis集成整合》《Vue.js使用》 ⛺️ 越努力 &#xff0c;越幸运。 1.Redis简介 1.1.什么是Redis Redis是一个开源&#xff08;BSD许可&#xff09;&#xff0c;内存存储的数据…
阅读更多...
unittest 通过TextTestRunner(buffer=True)打印断言失败case的输出内容

unittest 通过TextTestRunner(buffer=True)打印断言失败case的输出内容

buffer是unittest.TextTestRunner的一个参数&#xff0c;它决定了测试运行时是否将输出结果缓存&#xff0c;并在测试完成后一次性打印。 当buffer设置为True时&#xff0c;测试运行期间的输出结果会被缓存起来&#xff0c;并在测试完成后一次性打印。这对于一些输出频繁的测试…
阅读更多...
SPSS多因素方差分析

SPSS多因素方差分析

前言&#xff1a; 本专栏参考教材为《SPSS22.0从入门到精通》&#xff0c;由于软件版本原因&#xff0c;部分内容有所改变&#xff0c;为适应软件版本的变化&#xff0c;特此创作此专栏便于大家学习。本专栏使用软件为&#xff1a;SPSS25.0 本专栏所有的数据文件请点击此链接下…
阅读更多...
MongoDB安装及开发系例全教程

MongoDB安装及开发系例全教程

一、系列文章目录 一、MongoDB安装教程—官方原版 二、MongoDB 使用教程(配置、管理、监控)_linux mongodb 监控 三、MongoDB 基于角色的访问控制 四、MongoDB用户管理 五、MongoDB基础知识详解 六、MongoDB—Indexs 七、MongoDB事务详解 八、MongoDB分片教程 九、Mo…
阅读更多...
炸了！CVPR 2024投稿ID突破18000

炸了！CVPR 2024投稿ID突破18000

点击下方卡片&#xff0c;关注“CVer”公众号 AI/CV重磅干货&#xff0c;第一时间送达 点击进入—>【计算机视觉和Transformer】交流群 扫码加入CVer知识星球&#xff0c;可以最快学习到最新顶会顶刊上的论文idea和CV从入门到精通资料&#xff0c;以及最前沿项目和应用&…
阅读更多...
分析报告有样板了-奥威BI数据可视化报表模板

分析报告有样板了-奥威BI数据可视化报表模板

述职报告、月度数据分析报告、季度数据分析报告、区域数据分析报告……人在职场&#xff0c;数据分析报告少不了。那么&#xff0c;怎么才能在极短的时间内做出一张既好看又突出重点、分析逻辑在线的数据可视化分析报表&#xff1f;奥威BI软件的建议是采用BI数据可视化报表模板…
阅读更多...
0-1矩阵列互斥问题——回溯法 Python实现

0-1矩阵列互斥问题——回溯法 Python实现

三、 0-1 矩阵的列集互斥问题。给定一个 m n m \times n mn 的 0-1 矩阵 A \mathrm{A} A 。定义列互斥为: 对于矩阵 A A A 中的任意两列 i i i 和 j j j, 如果在对应的每一行上, i i i 和 j j j 不存在同时为 1 的情况, 则称列 i \mathrm{i} i 和 j \mathrm{j} j 互斥…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023