一、二分查找
1、前提条件:数据有序,随机访问;
2、实现:递归实现,非递归实现
3、注意事项:
循环退出条件:low <=high,low = high.说明还有一个元素,该元素还要与key进行比较
mid的取值:mid=(low + high)/2;mid = low + ((high - low)>>1)
low 和high 的更新:low = mid +1;high = mid - 1;不能写成low = mid +1,high = mid-1;又可能出现死循环;
代码实现:


1、查找第一个与key相等的元素:
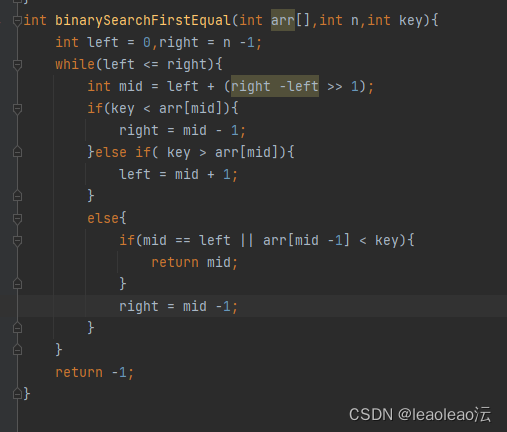
2、查找最后一个与key相等的元素

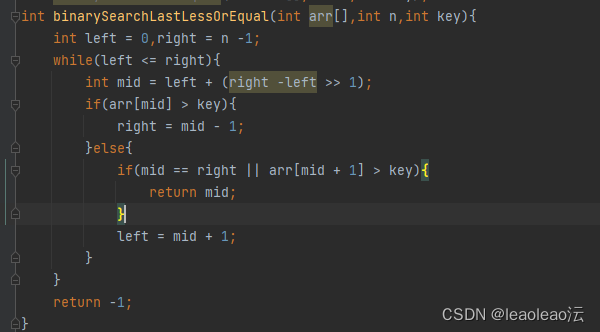
3、查找最后一个小于等于key值的元素
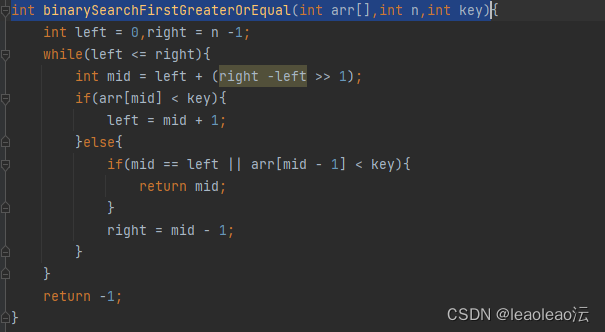
4、查找第一个大于等于key值的元素
二、冒泡排序
如何评价一个算法:
1、时间复杂度:最好情况;最坏情况;平均情况;系数和低阶项
2、空间复杂度:原地排序(特指空间复杂度为O(1))的排序;
3、稳定性:数据集中“相等”的元素,如果排序前和排序后的相对次序不变,那么这个排序就是稳定的;
稳定性就是排序算法的很重要的指标;
冒泡排序:
比较相邻的元素,如果前一个比后一个大,就交换次序,
对每一对相邻元素做同样的工作,从第一对到最后一对。最大的元素就会位于最后位置;
除最后一个元素外,对其他元素重复上面的步骤,直到元素的个数为1;
时间复杂度:
最好情况原数组有序(O(n));
最坏情况原数组逆序(比较次数(n-1)+(n-2)+...+1 = (n(n-1))/2)
交换次数:((n-1)+(n-2)+...+1 = (n(n-1))/2)
平均情况(每一种情况出现的情况是相等的):总情况(N!)
(比较次数:大于交换的次数,小于(n(n-1))/2)
(交换次数(n(n-1)/4))

分析:有序元素对,逆序元素对,逆序度,有序度;


有序对:34,24,14
逆序对:12,13,23
排序的过程:增加有序度,减少逆序度,最终达到满有序度;
冒泡排序交换导致有序度+1,逆序度-1;
空间复杂度:O(1);//原地排序
稳定性:稳定,arr[j]>arr[j+1] 才发生交换;

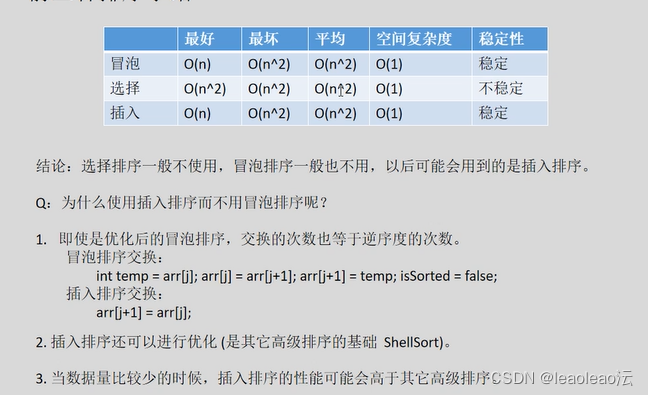
三、选择排序(无论什么数据进去都是(O(n2))的时间复杂度,所以用它的时候数据规模越小越好,唯一好处是不占用额外内存)
工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后再从剩余未排序中继续寻找最小(大)元素,然后放到已排序序列的末尾,以此类推,直到所有元素均排序完毕;(选择排序不能像冒泡排序一样去优化)
时间复杂度:O(n2)
比较次数:(n-1)+ ...+1 =(n(n-1))/2
交换次数:n-1;
空间复杂度:O(1)原地排序
稳定性:不稳定,发生了长距离的交换;

四、插入排序:
工作原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在从后向前扫描过程中,需要反复把已排序的元素逐步向后挪位,为最新元素提供插入空间;
时间复杂度:
最好情况:(O(n))
原数组有序(比较次数,(n-1))交换次数:原数组有序(0)
最坏情况:(O(n2))
原数组逆序(比较次数,(n-1)+(n-2)+...+1 = (n(n-1))/2);
交换次数((n-1)+(n-2)+...+1 =(n(n-1))/2:
平均情况:
比较次数:大于交换次数,小于(n(n-1))/2
交换次数:(n(n-1))/4(逆序个数)
插入排序好处,当元素基本有序时,其性能非常好;
空间复杂度,O(1),原地排序
稳定性:稳定;

冒泡排序,选择排序,插入排序小结:
五、希尔排序(缩小增量排序,插入排序的改进版本):
第一批打破O(n2)这个时间复杂度的方法;
gap(希尔):n/2、n/4、...1;
gap = n/2=5

先按gap分组,组内使用简单的插入排序(十个元素分为5组);

第一次组间排序完成后,就缩小增量,gap=5/2=2;gap =1;
时间复杂度比O(n2)小,和具体的gap序列相关;
空间复杂度O(1)原地排序;
稳定性:不稳定,会发生长距离交换;

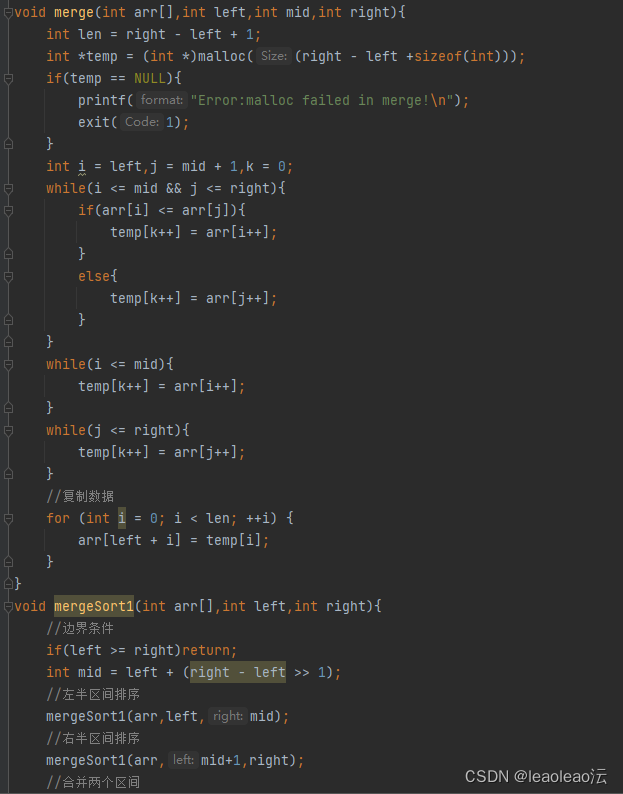
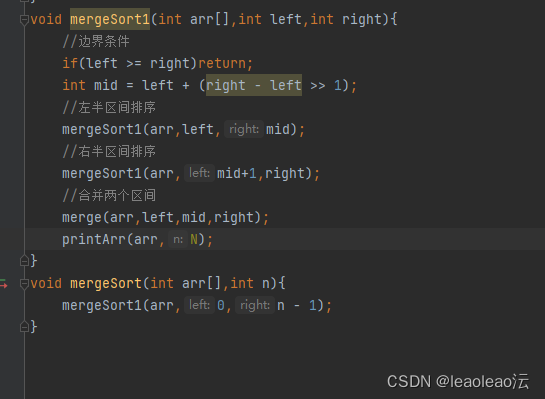
六、归并排序:
先把大数组分成两个小数组,直到有序再合并;单个数组已经算是有序的;
用递归解决;
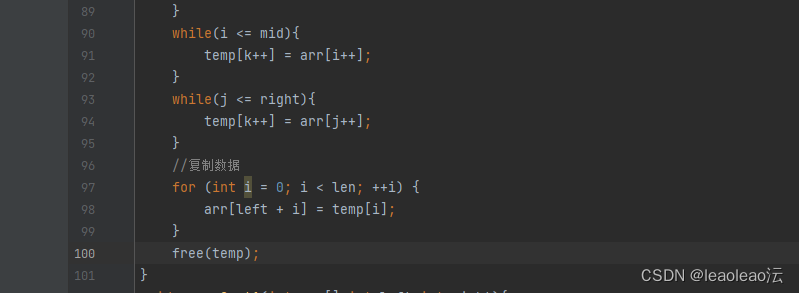
注意释放堆区数组


七、快速排序
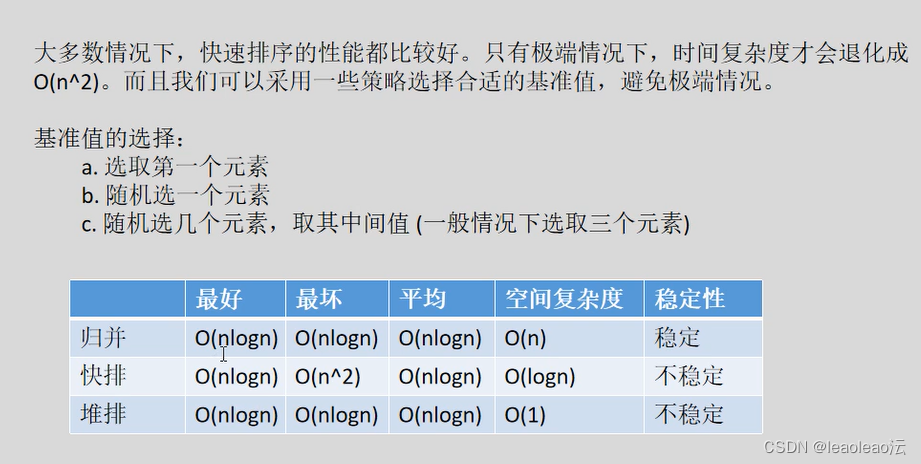
从数列中挑出一个元素,称为“基准”(pivot);(一般情况下可以选几个值取中位数,也可以选第一位,或者随机位)
重新排序数列,所有元素比基准值小的拜访在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任意边。)在这个分区退出后,改基准就处于数列的中间位置(也就是最终位置)这个操作我们称之为分区(partition);
递归地把小于基准值元素地子数列和大于基准值元素地子数列排序(左右两边都使用快排);

i 是放下一个比基准值小的位置,j放比基准值大的值;先移动 j 再移动 i ;
先找比基准值小的,再找比基准值大的,交替找直到 i j 相遇,基准值的位置就确定了;
因为基准值已经保存就可以移动 j 把第一个值覆盖掉(以第一个值为基准)

时间复杂度:
最好情况:(每次分区都分成大小相等的两份)![]()

最坏情况:每次基准值都位于最左边或者最右边;
![]()

平均情况(假设每次分成三比一的情况):
![]()

空间复杂度:![]()


快速排序的改进策略(基准值的选取(随机选,选择多个元素的中位数);分区操作的优化;选择多个基准值);
八、堆排序
二叉堆(大顶堆(根节点的键大于左右子树所有结点的键,并且左右子树都是大顶堆);小顶堆(根节点的键小于左右子树所有结点的键,并且左右子树都是小顶堆))

把数组看作一个完全二叉树;

堆排算法:
把完全二叉树构建成大顶堆,找到第一个非叶子结点,从后往前构建大顶堆
把堆顶元素和无序区的最后一个元素交换,交换之后无序区的长度减一,
把无序区重新调整成大顶堆,重复上一步操作,直到无序区的长度为1;


归并(缺点:占用内存空间复杂度O(n)),快排,堆排
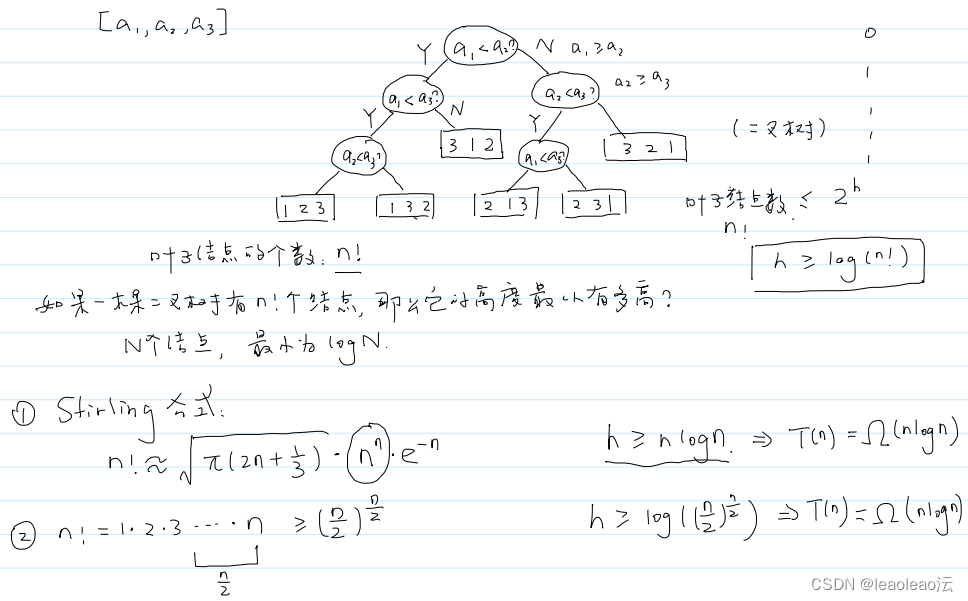
九、基于比较的排序算法
证明:基于比较 的排序算法,时间复杂度的下限就是O(nlogn);