枚举求强于其他所有队的队

class Solution {
public:int findChampion(vector<vector<int>> &grid) {int n = grid.size();int res = 0;for (int i = 0; i < n; i++) {int t = 0;for (int j = 0; j < n; j++)if (j != i)t += grid[i][j];if (t == n - 1) {res = i;break;}}return res;}
};

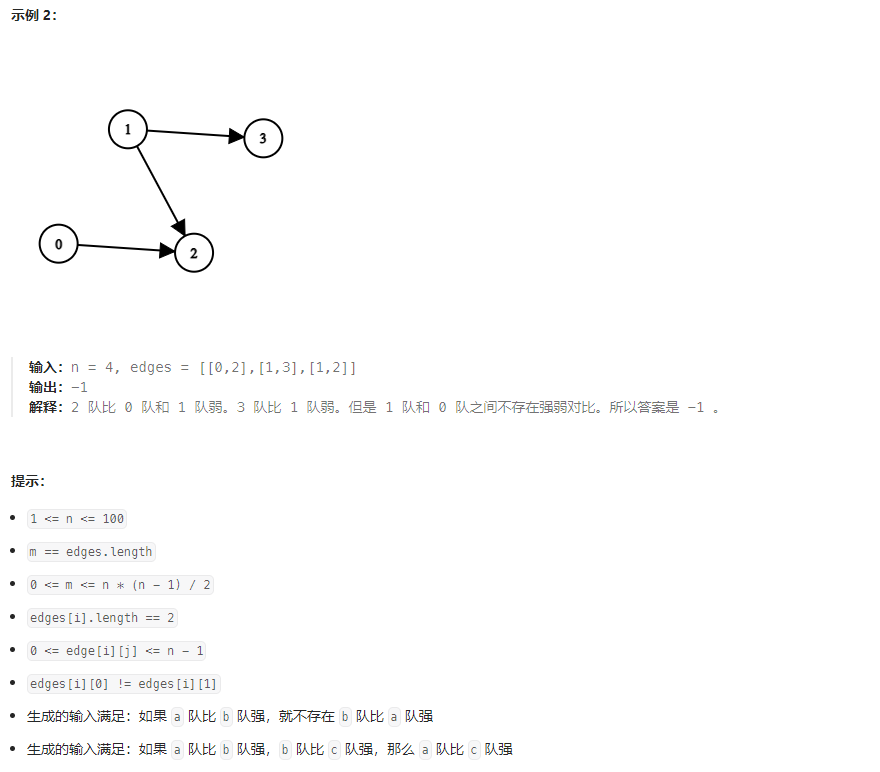
计数：若图中入度为 $0$ 的点只有一个则该点为冠军，否则返回 $-1$

class Solution {
public:int findChampion(int n, vector<vector<int>> &edges) {vector<int> indeg(n);for (auto &ei: edges)indeg[ei[1]]++;vector<int> li;for (int i = 0; i < n; i++)if (indeg[i] == 0)li.push_back(i);if (li.size() != 1)return -1;return li[0];}
};

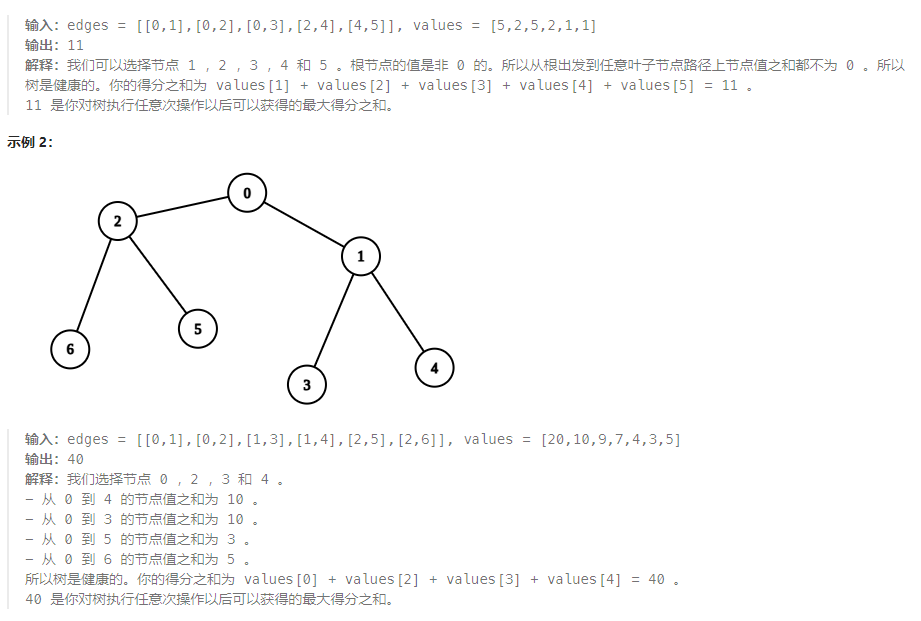
动态规划：设 $p[cur][0]$ 为在以 $cur$ 为根的子树上执行若干操作使得该子树是健康的 能得到的最大分数，设 $p[cur][1]$ 为以 $cur$ 为根的子树各节点 $values$ 之和，有状态转移方程： p [ c u r ] [ 0 ] = { 0 , c u r 是叶子节点 m a x { v a l u e s [ c u r ] + ∑ j 是 c u r 的子节点 p [ j ] [ 0 ] , ∑ j 是 c u r 的子节点 p [ j ] [ 1 ] } , c u r 不是叶子节点 p[cur][0]=\left\{\begin{matrix} 0 & ,cur 是叶子节点\\ max\{ values[cur]+\sum_{j 是 cur的子节点} p[j][0],\;\sum_{j 是 cur的子节点} p[j][1] \} &,cur 不是叶子节点 \end{matrix}\right. p[cur][0]={0max{values[cur]+∑j是cur的子节点​p[j][0],∑j是cur的子节点​p[j][1]}​,cur是叶子节点,cur不是叶子节点​

class Solution {
public:using ll = long long;long long maximumScoreAfterOperations(vector<vector<int>> &edges, vector<int> &values) {int n = edges.size() + 1;vector<int> e[n];for (auto &ei: edges) {e[ei[0]].push_back(ei[1]);e[ei[1]].push_back(ei[0]);}ll p[n][2];memset(p, -1, sizeof(p));//初始化状态function<ll(int, int, int)> get = [&](int cur, int type, int par) {//记忆化搜索if (p[cur][type] != -1)return p[cur][type];if (type == 0) {if (cur != 0 && e[cur].size() == 1)return p[cur][type] = 0;ll r1 = 0, r2 = values[cur];for (auto j: e[cur])if (j != par) {r1 += get(j, 1, cur);r2 += get(j, 0, cur);}return p[cur][type] = max(r1, r2);} else {ll r2 = values[cur];for (auto j: e[cur])if (j != par)r2 += get(j, 1, cur);return p[cur][type] = r2;}};return get(0, 0, 0);}
};

动态规划 + 离散化 + 树状数组：设数组 $c[i]=nums[i]-i$ ，则 $c$ 数组中非降序子序列的下标序列即为平衡子序列，所有可以对 $c$ 数组进行离散化，然后定义状态 $p[i]$ 为：$c$ 数组中末尾元素为 $i$ 的非降序子序列对应的平衡子序列在 $nums$ 中的最大和，有状态转移方程： p [ i ] = m a x { n u m s [ i ] m a x { p [ j ] ∣ j ≤ i } + n u m s [ i ] p[i]=max\left\{\begin{matrix} nums[i]\\ max\{p[j] \;|\; j\le i \}+nums[i] \end{matrix}\right. p[i]=max{nums[i]max{p[j]∣j≤i}+nums[i]​ ，通过树状数组实现其中的前缀极值查询和单点更新

class Solution {
public:using ll = long long;int N;vector<ll> a;inline int lowbit(int x) {return x & -x;}void update(int loc, ll val) {// li[loc]=max(li[loc], val);for (; loc < N; loc += lowbit(loc))a[loc] = max(a[loc], val);}ll query(int loc) {// max{li[k] | 1<=k<=loc}ll res = INT64_MIN;for (; loc > 0; loc -= lowbit(loc))res = max(res, a[loc]);return res;}long long maxBalancedSubsequenceSum(vector<int> &nums) {int n = nums.size();vector<int> c(n);for (int i = 0; i < n; i++)c[i] = nums[i] - i;vector<int> t = c;sort(t.begin(), t.end());t.erase(unique(t.begin(), t.end()), t.end());for (int i = 0; i < n; i++)//离散化cc[i] = lower_bound(t.begin(), t.end(), c[i]) - t.begin();N = n + 1;a = vector<ll>(N, INT64_MIN);for (int i = 0; i < n; i++) {ll t1 = query(c[i] + 1);update(c[i] + 1, max(t1, 0LL) + nums[i]);}return query(n);}
};