一、引入多维特征
在多维特征中,我们考虑的不再是单一的特征,而是一组特征,例如房价模型中可能包括房间数、楼层等多个特征。这些特征将组成一个向量,表示为(𝑥₁, 𝑥₂, . . . , 𝑥ₙ),其中 𝑛 代表特征的数量。每个特征都可以表示数据集中的不同属性。

对于每个训练实例,我们使用向量表示特征,如𝑥(𝑖) = [1416, 3, 2, 40],这里 𝑥ⱼ(𝑖) 代表特征矩阵中第 𝑖 行的第 𝑗 个特征,也就是第 𝑖 个训练实例的第 𝑗 个特征。
支持多变量的假设 ℎ 表示为:
ℎ𝜃(𝑥) = 𝜃₀ + 𝜃₁𝑥₁ + 𝜃₂𝑥₂ + . . . + 𝜃ₙ𝑥ₙ
在这个公式中,有 𝑛 + 1 个参数和 𝑛 个变量。为了简化这个公式,我们引入 𝑥₀ = 1,这将使公式转化为:
ℎ𝜃(𝑥) = 𝜃₀𝑥₀ + 𝜃₁𝑥₁ + 𝜃₂𝑥₂ + . . . + 𝜃ₙ𝑥ₙ
这样,模型中的参数是一个 𝑛 + 1 维的向量,每个训练实例也都是一个 𝑛 + 1 维的向量,特征矩阵 𝑋 的维度是 𝑚 × (𝑛 + 1)。

二、多变量梯度下降
与单变量线性回归类似,多变量线性回归中也需要构建代价函数。代价函数表示为所有建模误差的平方和:
𝐽(𝜃₀, 𝜃₁, . . . 𝜃ₙ) = 1/2𝑚 ∑ (ℎ𝜃(𝑥(𝑖)) - 𝑦(𝑖))², 其中 ℎ𝜃(𝑥) = 𝜃₀ + 𝜃₁𝑥₁ + 𝜃₂𝑥₂ + . . . + 𝜃ₙ𝑥ₙ
我们的目标仍然是找出使代价函数最小化的一系列参数。多变量线性回归的批量梯度下降算法为:

不断迭代,更新参数𝜃₀, 𝜃₁, . . . , 𝜃ₙ,直到收敛。
三、特征缩放
在处理多维特征问题时,确保所有特征具有相近的尺度是非常重要的。如果特征的尺度差异太大,会导致梯度下降算法收敛缓慢。通常,我们将所有特征的尺度缩放到 -1 到 1 之间,这有助于加速梯度下降的收敛。

最简单的方法是将每个特征缩放为:
𝑥ₙ = (𝑥ₙ - 𝜇ₙ) / 𝑠ₙ
其中 𝜇ₙ 是特征的均值,𝑠ₙ 是标准差。这样,所有特征都具有相似的尺度,有助于算法更快地收敛。

四、学习率
梯度下降算法的学习率(learning rate)是一个关键的超参数,对于算法的性能和收敛速度具有重要影响。学习率决定了每次参数更新的步长,过小的学习率可能导致算法收敛得非常慢,而过大的学习率可能使得算法无法收敛。

-
小学习率(例如 0.01 或 0.03):这些学习率通常使算法非常稳定,但可能需要更多的迭代才能收敛到最佳解。
-
适中的学习率(例如 0.1 或 0.3):这些学习率通常是一个好的起点,可以使算法在相对较少的迭代次数内收敛到较好的解。
-
大学习率(例如 1、3 或 10):这些学习率可能使算法在较少的迭代次数内快速收敛,但如果学习率过大,可能会导致算法不收敛,甚至发散。
通常,选择合适的学习率需要进行试验和调整。可以开始尝试中等大小的学习率,然后根据算法的表现逐渐调整。同时,可以使用学习率衰减策略,随着迭代次数的增加逐渐减小学习率,以平衡速度和稳定性。

五、特征与多项式回归
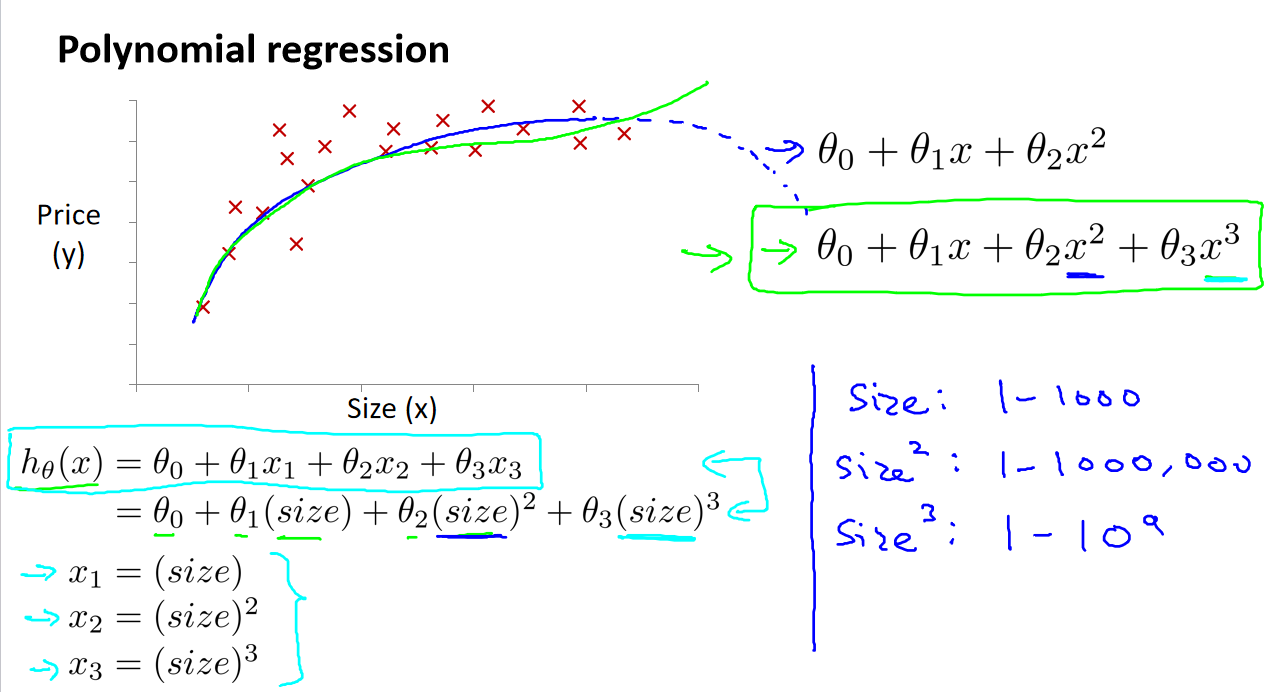
在某些情况下,线性回归模型可能无法很好地拟合数据,因为数据的关系不是线性的。多项式回归是一种技术,用于处理这些情况。它允许引入更高次的特征,以拟合数据的曲线形状。
-
多项式回归模型:这是线性回归的一种扩展,允许使用多项式函数来拟合数据。模型的形式可以是像这样的方程:ℎ𝜃(𝑥) = 𝜃₀ + 𝜃₁𝑥₁ + 𝜃₂𝑥₂ + . . . + 𝜃ₙ𝑥ₙ,其中 n 是多项式的次数。
-
特征变换:除了多项式回归,特征变换也是一种方法。通过对原始特征进行变换,例如取对数、开方、指数等,可以使问题更适合线性回归模型。这样的变换可以将非线性关系转化为线性关系。
在实际应用中,选择多项式次数或特征变换的方法需要根据数据的特点进行试验和调整。通常,我们会观察数据的分布和关系,然后根据需要决定是否采用多项式回归或特征变换,以获得更好的拟合结果。
参考资料:
[中英字幕]吴恩达机器学习系列课程
黄海广博士 - 吴恩达机器学习个人笔记